本章節介紹曲綫的不同表示方式，從多項式曲綫開始，到貝塞爾曲綫，最後是更一般的B-樣條曲綫，文中分析了各種曲綫的優缺點，以及圖形學中常用的幾種曲綫表示。

15.1 Curves

對於曲綫直觀上可以描述為一段時間内一個點的運動軌跡。而在數學上，至少有以下兩種描述方式：

n維空間中，某個區間的連續圖像；
從一維空間到n維空間的連續映射。

這些描述中的共同點是都利用了區間間隔的思想，但不同點在於，第一種描述（包括直觀上的描述）的本質都是點的集合；第二種描述本質則是點或時間的映射。本章節中將采用第一種描述方式。基於這種方式，我們可知，曲綫是一個無窮大的點集合，除去端點上的點只有一個“鄰居”外（除非該曲綫是封閉的，或是直綫），其他點均有兩個"鄰居“。

在數學上定義曲綫的方式有下面三種形式：

Implicit - 隱式表示法 $$ f(x,y) = 0 $$

滿足上述等式的所有點的集合即爲曲綫。例如，圓的隱式表示如下： $$ f(x,y) = x^2 + y^2 - 1 = 0 $$

Parametric - 參數表示法，該表示法是從某個自由參數到曲綫上點的映射，即自由參數為曲綫上的點提供了一個索引。最常見的就是圓的參數表示：

$$ \begin{cases} x = \cos{\theta}\\ y = \sin{\theta} \end{cases}, \ \theta \in [0, 2\pi) $$

跟一般的寫法是：

$$ (x,y) = f(t) $$

Generative or Procedual - 生成式或過程曲綫。

注意，任意一條曲綫都可能有多種數學表示，所以在數學上會謹慎的區別曲綫和它的表示。但是在圖形學中，我們通常只關心它的表示方式而不是曲綫本身。

不同的表示方式有各自優缺點。

1
2
3
4
5
6
7


隱式表示：
* 優點：使用方便，容易驗證某個點與曲綫的關係；
* 缺點：不直觀，在圖形上采樣難度大。

參數表示：
* 優點：容易繪製，在圖形上采樣容易；
* 缺點：參數表示方程獲取難度較大；對於點與曲綫關係判斷難度大。

基於它們的優缺點，在圖形學中通常會使用參數化的表示方式。

15.1.1 Parameterization and Reparameterizations

在使用參數化曲綫時，本質是將一段區間通過指定的參數做映射。通常我們規定區間為單位區間：[0,1]；指定的參數用$u$表示。

定義某曲綫為：

$$ \mathcal{C}: f(t), t\in[a, b] $$

這稱爲曲綫的參數化(parameterization)。

假設，參數$t$滿足$t = g(u), u\in[a’, b’]$，則：

$$ \mathcal{C}: f_2(u) = f(t) = f(g(u)), u \in [a', b'] $$

這稱爲曲綫的重新參數化。重新參數化中，從舊參數到新參數的映射成爲重新參數化函數。

從曲綫參數化和重新參數化中可以驗證，表示曲綫的方式可以有無窮多種；而重新參數化的好處是可以找到一種方便的參數化形式；而缺點也很明顯，就是很難比較兩個函數是否表示同一條曲綫。另一個更嚴重的問題是自由參數會導致不可見的未知要素。例如下面三種形式在相同區間表示同一條曲綫，但是，除去起點和終點外其他位置是不同的。

$$ \begin{align} (x,y) &= f(u) = (u, u) \\ (x,y) &= f(u) = (u^2, u^2) \\ (x,y) &= f(u) = (u^5, u^5) \end{align} $$

接下來引入Natrual Parameterization（自然參數化）的概念，所謂自然參數化，個人理解就是，能夠用有物理解釋的參數，例如，曲綫的弧長，物體的速度等。下面用曲綫弧長舉例詳細説明。

弧長參數化，通過沿著曲綫的長度（弧長）映射到曲綫上位置的函數定義。技術上講，就是其切綫斜率大小為定值，即：

$$ \left| \frac{\mathrm{d}\mathbf{f}(s)}{\mathrm{d}s}\right|^2 = c $$

而計算弧長通常是由導數大小的積分定義（導數大小為沿曲綫運動的速度）。這樣就可定義弧長為： $$ s = \int_{0}{v}\left|\frac{\mathrm{d}\mathbf{f}(t)}{\mathrm{d}t}\right|^2 \mathrm{d}t \tag{15.1} $$

其中，$s$為弧長，$\mathbf{f}(t)$是一個用自然參數化定義的曲綫函數。

要利用弧長參數化表示，需要利用等式(15.1)，給定$s$求解$t$。通常是沒有解析解，需要通過數值方式獲得。

15.1.2 Piecewise Parametric Representations

對於一些曲綫，利用參數化能很容易表示処其形狀，例如直綫，圓，橢圓等，但大多數曲綫找到其對應形狀的函數是非常困難的。因此，我們采用“分而治之”的方式處理，將曲綫拆分成多個片段，每個片段都能用一些簡單的曲綫表示。如下圖所示。

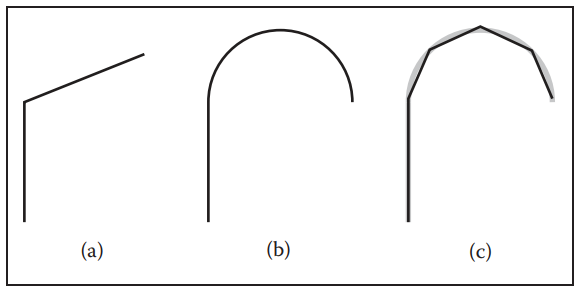
圖中(a)，(b)可以用如下形式表示：

$$ \mathbf{f}(u) = \begin{cases} \mathbf{f}_1(2u), & if\ u \leq 0.5 \\[2ex] \mathbf{f}_2(2u - 1), & if \ u > 0.5 \end{cases} \tag{15.2} $$

同時要保證$\mathbf{f}_1$和$\mathbf{f}_2$相吻合，如果$\mathbf{f}_1(1) \neq \mathbf{f}_2(0)$，那麽就無法形成一條連續的曲綫。此外，像圖(b)中所示，是由兩種不同類型的曲綫組合而成，而有時我們只希望使用一種類型，那麽這裏就需要重構曲綫，例如上圖(c)中那樣，用有限根直綫逼近半圓，雖然這種方式不夠準確，但是也足夠我們使用，關鍵是它的表示方式能夠足夠簡單。

利用分段表示的好處有以下幾點：

能夠根據需要來調整曲綫的逼近程度；
能夠控制每個分段的複雜程度；
能夠控制分段的數量；

圖形學中傾向於使用簡單的曲綫片段，例如綫段、弧或多項式曲綫等。

15.1.3 Splines（樣條）

Spline是電腦出現前，繪圖員利用可彎曲的金屬片進行連續曲綫繪製，這種金屬片就用spline表示，稱爲曲綫尺。之後，數學家發現可以用分段多項式函數進行仿真，所以引用spline一詞，將它表示爲平滑的分段多項式函數，簡稱“樣條”。對於我們而言，樣條就是指分段多項式函數，這樣的函數對於表示曲綫是非常有用的。

15.2 Curve Properties

下面説説曲綫的一些屬性，不同類型的曲綫都有一些自己特有的屬性，例如橢圓的屬性有其長短軸比例和主軸方向。對於任意形式的曲綫，我們需要更一般的屬性對其進行描述，我們又將這些屬性分爲兩類，一是局部屬性(local properties)，另一個是全局屬性(global properties)。

下面重點研究曲綫的局部屬性，它包含以下幾個方面：

連續性；
曲綫上具體地方的位置；
曲綫上具體地方的方向；
曲率（和其他導數）。

當我們指定曲綫必須包含某個特定點時，就稱爲曲綫插值了一個點，即$f(t) = v$，其中$t$表示插值位置。

15.2.1 Continuity

通常，我們使用$C^{n}$來表示曲綫的連續性，其含義是在曲綫片段閒所有導數直到$n$階導數都能匹配。以等式(15.2)舉例，$C^{0}$表示$\mathbf{f}_{1}(1) = \mathbf{f}_2(0)$；$C^{1}$表示$\mathbf{f}_1’(1) = \mathbf{f}_2’(0)$；以此類推至$n$。下圖展示了不同階連續的曲綫樣式。

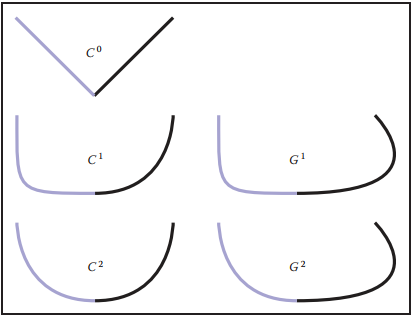
$C^n$連續我們可以稱爲參數連續，其依賴兩條曲綫的參數化，但是由於相同曲綫能用不同參數形式表示，這會導致不同參數表示時，兩條曲綫可能是不連續的。爲了避免這種情況，又定義了幾何連續概念，其要求兩條曲綫在相同參數化形式下（最直觀的就是利用自然參數化形式）具有相匹配的導數，它只需要有相同的方向，大小存在一定比例關係。

這樣，對比$C^{1}$和$G^{1}$:

$$ \begin{align} C^{1}: \ \mathbf{f}_1'(1) &= \mathbf{f}_2'(0) \\[2ex] G^{1}: \ \mathbf{f}_1'(1) &= k\ \mathbf{f}_2'(0) \end{align} $$

其中，$k$表示比例係數。由於參數連續要比幾何連續更嚴格，所以$G^{n}$是$C^{n}$的必要條件，反之不成立。

15.3 Polynomial Pieces

本節將介紹圖形學中常用的幾種曲綫片段表示，由於它們都可用多項式表示，所以稱爲多項式片段。

15.3.1 Polynomial Notation

多項式表示形式如下： $$ f(t) = a_0 + a_1 t + a_2 t^2 + \cdots + a_n t^n \tag{15.3} $$

其中，$a_i$表示多項式係數，$n$稱爲多項式階數($a_n \neq 0$)。等式(15.3)也可用如下形式表示： $$ f(t) = \sum_{i = 0}^{n}a_it^i \tag{15.4} $$

我們稱(15.4)為多項式的標準形式。另外更一般的寫法是： $$ f(t) = \sum_{i = 0}^{n}\mathbf{c}_ib_i(t) \tag{15.5} $$

其中，$b_i(t)$是一個多項式，可以根據不同應用選擇方便處理的形式，我們稱這些多項式為基函數或是混合函數。假設正確選擇了基函數，可以選擇適當的$\mathbf{c}$表示任意的$n+1$次多項式。

15.3.2 A Line Segment

通常綫段會用兩個端點表示，$\mathbf{p}_0$和$\mathbf{p}_1$。其參數方程為： $$ \mathbf{f}(u) = (1-u)\mathbf{p}_0 + u\mathbf{p}_1 \tag{15.6} $$

我們將$\mathbf{p}$稱爲控制點。

描述綫段的方式除了使用首尾端點描述外，還有如下形式：

綫段中心位置、綫段方向、綫段長度；
綫段一個端點位置，以及另一個端點的相對位置；
綫段中心位置及一個端點。

這些描述方式閒是可以相互轉換的。

另一種表示綫段的方式是使用多項式標準型： $$ \mathbf{f}(u) = \mathbf{a}_0 + u \mathbf{a}_1 \tag{15.7} $$

任意綫段都能通過指定$\mathbf{a}_0$和$\mathbf{a}_1$表示，通常我們使用兩個端點，它們能容易的推出其他參數形式。

回顧等式(15.4)，將其改爲向量形式，令$\mathbf{u} = [1\ u\ u^2\ u^3\ \cdots\ u^n]$，則： $$ \mathbf{f}(u) = \mathbf{u} \cdot \mathbf{a} \tag{15.8} $$

等式(15.8)被稱爲規範形式，參數記爲$\mathbf{a}$。這種向量表示法將使曲綫不同形式閒的轉換更容易。雖然這種方式在數學上非常簡單，但不一定是表示曲綫的最方便的形式。例如，以綫段舉例，用兩個端點定義一條直綫，令$\mathbf{p}_0$表示起點，$\mathbf{p}_1$表示終點，那麽我們可以根據等式(15.8)得到如下形式：

$$ \begin{align} p_0 = f(0) = [1\ 0] \cdot [a_0\ a_1]\\[2ex] p_1 = f(1) = [1\ 1] \cdot [a_0\ a_1] \end{align} \tag{15.9} $$

求解這個方程組，我們可以得到$a_0$和$a_1$為：

$$ \begin{align} a_0 &= p_0\\ a_1 &= p_1 - p_0 \end{align} $$

我們將其改下成矩陣形式：

$$ \begin{bmatrix} p_0\\ p_1 \end{bmatrix} = \begin{bmatrix} 1&0\\ 1&1 \end{bmatrix} \begin{bmatrix} a_0\\ a_1 \end{bmatrix}\\[2ex] \Rightarrow \mathbf{p} = \mathbf{C}\mathbf{a} $$

其中，$\mathbf{C}$稱爲約束矩陣，其逆矩陣用$\mathbf{B}$表示，稱爲基矩陣。基矩陣是非常方便的，它告訴我們好用的參數$\mathbf{p}$與標準型$\mathbf{a}$之間是如何轉換的，這樣我們就能得到以下形式。 $$ \mathbf{f}(u) = \mathbf{u}\mathbf{B}\mathbf{p} \tag{15.10} $$

對於參數定義中沒有非綫性關係的任何形式曲綫，都可以找到一個基矩陣。非綫性定義的參數有綫段長度和角度等。

15.3.3 Beyond Line Segments

對於等式(15.4)，定義更複雜曲綫的方式只需要將$n$值變大即可。下面以二次多項式爲例，其包含係數$\mathbf{a}_0$、$\mathbf{a}_1$和$\mathbf{a}_2$，這些係數無法直觀反映曲綫的形狀，但是通過基矩陣的方式，我們可以找到一些更有效的參數表示。

通常我們求解二次多項式係數都通過三個點位置求解得到，例如$u = 0$、$u = 0.5$和$u = 1$，帶入等式(15.4)得到：

$$ \begin{array}{l} \mathbf{p}_0 &= \mathbf{f}(0) &= \mathbf{a}_0 + 0^1\ \ \ \mathbf{a}_1 + 0^2\ \ \ \mathbf{a}_2\\ \mathbf{p}_1 &= \mathbf{f}(0.5) &= \mathbf{a}_0 + 0.5^1\mathbf{a}_1 + 0.5^2\mathbf{a}_2\\ \mathbf{p}_2 &= \mathbf{f}(1) &= \mathbf{a}_0 + 1^1\ \ \ \mathbf{a}_1 + 1^2\ \ \ \mathbf{a}_2 \end{array} $$

其約束矩陣為：

$$ \mathbf{C} = \begin{bmatrix} 1 & 0 & 0\\ 1 & .5 & .25\\ 1 & 1 & 1 \end{bmatrix} $$

推導出基矩陣為：

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 1 & 0 & 0\\ -3 & 4 & -1\\ 2 & -4 & 2 \end{bmatrix} $$

上面是一般性做法得到的基函數，其形式不夠簡單。現在我們換個想法，通常我們知道對於曲綫函數，其一階導數表示曲綫的方向，其二階導數表示曲綫方向變化的快慢。對於二次多項式曲綫，其一、二階導數如下：

$$ \begin{align} \mathbf{f}(u) &= \mathbf{a}_0 + \mathbf{a}_1u + \mathbf{a}_2u^2\\[2ex] \mathbf{f}'(u) &= \frac{\mathrm{d}\mathbf{f}}{\mathrm{d}{u}} = \mathbf{a}_1 + 2\mathbf{a}_2u\\[2ex] \mathbf{f}''(u) &= \frac{\mathrm{d}^2\mathbf{f}}{\mathrm{d}u^2} = \frac{\mathrm{d}\mathbf{f}'}{\mathrm{d}u} = 2\mathbf{a}_2 \end{align} $$

對於等式(15.4)，更通用的一、二階導數如下：

$$ \begin{align} \mathbf{f}'(u) &= \sum_{i=1}^{n}i\ u^{i-1}\mathbf{a}_i\\ \mathbf{f}''(u) &= \sum_{i=1}^{n}i(i-1)\ u^{i-2}\mathbf{a}_i \end{align} $$

此時，我們考慮$u= 0.5$位置，利用該位置一、二階導數信息得到約束矩陣和基矩陣為：

$$ \begin{array}{l} \mathbf{p}_0 &= \mathbf{f}(0.5) &= \mathbf{a}_0 + 0.5^1\mathbf{a}_1 + \ \ \ \ \ \ 0.5^2\ \ \ \mathbf{a}_2\\ \mathbf{p}_1 &= \mathbf{f}'(0.5) &= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{a}_1 + 2\ *\ 0.5\ \ \ \mathbf{a}_2\\ \mathbf{p}_2 &= \mathbf{f}''(0.5) &= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\ \ \ \ \ \mathbf{a}_2 \end{array} $$

$$ \mathbf{C} = \begin{bmatrix} 1 & .5 & .25\\ 0 & 1 & 1\\ 0 & 0 & 2 \end{bmatrix} $$

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 1 & -.5 & .125\\ 0 & 1 & -.5\\ 0 & 0 & .5 \end{bmatrix} $$

這種方式形成的基矩陣就爲一個上三角矩陣，明顯比之前的基矩陣應用起來方便。

15.3.4 Basis Matrices for Cubics

三次多項式在圖形學中有廣汎應用，在之後的章節也會詳細介紹，這裏給出它的一種基函數表示形式——Hermite型，其只考慮兩個位置及其一階導數。

$$ \begin{array}{l} \mathbf{p}_0 &= \mathbf{f}(0) &= \mathbf{a}_0 + \ \ \ 0^1\ \mathbf{a}_1 + \ \ \ \ \ \ 0^2\ \mathbf{a}_2 + \ \ \ \ \ \ 0^3\ \mathbf{a}_3\\ \mathbf{p}_1 &= \mathbf{f}'(0) &= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{a}_1 + 2 * 0^1\ \mathbf{a}_2 + 3 * 0^2\ \mathbf{a}_3\\ \mathbf{p}_2 &= \mathbf{f}(1) &= \mathbf{a}_0 + \ \ \ 1^1\ \mathbf{a}_1 + \ \ \ \ \ \ 1^2\ \mathbf{a}_2 + \ \ \ \ \ \ 1^3\ \mathbf{a}_3\\ \mathbf{p}_3 &= \mathbf{f}'(1) &= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{a}_1 + 2 * 1^1\ \mathbf{a}_2 + 3 * 1^2\ \mathbf{a}_3 \end{array} $$

約束矩陣為：

$$ \mathbf{C} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 1 & 1 & 1\\ 0 & 1 & 2 & 3 \end{bmatrix} $$

基矩陣為：

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ -3 & -2 & 3 & -1\\ 2 & 1 & -2 & 1 \end{bmatrix} $$

15.3.5 Blending Functions(混合函數)

利用基函數，我們可以將曲綫函數改寫成(15.10)形式，那麽我們令：

$$ \mathbf{b}(u) = \mathbf{u}\mathbf{B} $$

該函數$\mathbf{b}(u)$的含義在於它定義了如何將控制點向量值混合，因此被稱爲混合函數。那麽一個完整的曲綫可以表示爲：

$$ \mathbf{f}(u) = \sum_{i = 0}^{n}\mathbf{b}_i(u)\mathbf{p}_i \tag{15.11} $$

我們可以看出，這是一個綫性方程，它定義了控制點的綫性混合(加權平均)，無論$\mathbf{b}_i$函數中的多項式次數如何，該方程都是成立的。

混合函數為描述曲綫提供了一個非常好的抽象。任何形式的曲綫都能通過綫性組合控制點形式獲得，而它們的權值可以作爲自由參數的任意函數來計算。

15.3.6 Interpolating Polynomials

根據之前的介紹，對於一個階數為$n$的多項式進行插值，我們需要$n+1$個控制點，則基函數可以寫爲： $$ f(t) = \sum_{i = 0}^{n}\mathbf{p}_ib_i(t) $$

$f(t)$表示某一個控制點得到的一個基函數，我們需要對$n+1$個基函數求解就能得到最終插值得到的多項式。對於基函數中$b_i(t)$可以有很多種表示方式，例如$b_i(t) = t^i$。但是最常用的是拉格朗日形式： $$ b_i(t) = \prod_{j = 0, j\neq i}^{n} \frac{t - p_j}{p_i - p_j} $$

拉格朗日插值形式在計算效率上更有優勢。

15.4 Putting Pieces Together

之前章節已經説明單獨的曲綫片段如何生成，本節將説明如何將這些片段聯合成一條完整曲綫。

15.4.1 Knots - 節點

由於曲綫是由多條片段連接而成，那麽每個片段的起點與終點就被稱爲節點。

以下圖中兩條綫段連接爲例説明。

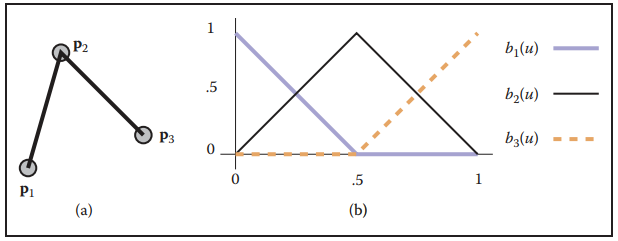
對於圖(a)中的綫段，我們可以寫爲：

$$ \mathbf{f}(u) = \begin{cases} \mathbf{f}_1(2u) & if\ 0 \leq u < \frac{1}{2} \\[2ex] \mathbf{f}_2(2u-1) & if \ \frac{1}{2} \leq u < 1 \end{cases} \tag{15.12} $$

它的節點為：$0$、$0.5$和$1$。

我們還可以用基函數和的形式寫出：

$$ \mathbf{f}(u) = \mathbf{p}_1b_1(u) + \mathbf{p}_2b_2(u) + \mathbf{p}_3b_3(u)\tag{15.13} $$

混合表示的這種方式我們需要對$b_i(u)$進行分段討論，例如，

$$ \begin{align} b_1(u) &= \begin{cases} 1 - 2u, & if \ 0 \leq u < \frac{1}{2}\\[2ex] 0, & otherwise \end{cases} \\[2ex] b_2(u) &= \begin{cases} 2u, & if \ 0 \leq u < \frac{1}{2}\\[2ex] 2-2u, & if \ 0.5 \leq u < 1 \end{cases}\\[2ex] b_3(u) &= \begin{cases} 2u-1, & if \ 0.5 \leq u < 1\\[2ex] 0, & otherwise \end{cases} \end{align} $$

15.4.2 Using Independent Pieces

之前我們定義每個多項式片段都是在單位區間内，儅把不同片段組合成同一條曲綫時，需要進行調整，最簡單的方式是在參數範圍$[0,n]$内定義曲綫，其中$n$為分段數目，之後根據參數值將其移動到需要的範圍内。

15.4.3 Putting Segments Together

有以下三種方式連接兩個曲綫片段：

shared-point策略，定義兩個片段端點為同一個點；
dependency策略，將第一個片段的終點作爲第二個片段起點，并且會隨著第一個片段參數變化而變化；
顯示定義連接點出方程，參數變化時通過數值計算獲得。

我們通常喜歡使用簡單的方式，但這也意味著參數化過程有更多的限制。例如，利用綫段起點和中點來定義綫段時，其連接方式就必須使用依賴策略。這就引出此時使用依賴策略的一個缺點，缺乏局部性。

所謂局部性就是，儅曲綫上某個點發生移動時，其只會影響一個局部範圍。這個局部的範圍可以很大，但是有限的，如果曲綫的控制點不具備局部性，那麽這一變化會影響到無限遠處的控制點。

比較下圖中，多個綫段不同表示方式下，其局部性表現。

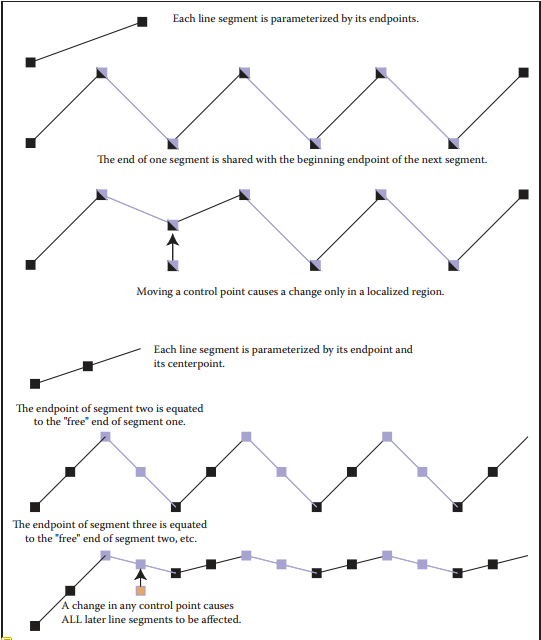
注意，依賴策略并不一定都不具有局部性，而共享策略也并不一定都具有局部性。局部性對於控制具有方便性，雖然對修改整條曲綫不方便，但是只需要移動多個點就能將相同變化作用在曲綫上。

15.5 Cubics

圖形學中，我們常使用綫段或三次多項式來表示曲綫片段，這麽做的原因有以下幾點。

三次多項式具有$C^2$連續性，能滿足大部分視覺任務；
三次多項式提供最小曲率插值；
三次多項式有完美的對稱性，曲綫的位置和導數都能在起始和終點位置指定；
三次多項式能在計算複雜度與曲綫平滑性之間進行權衡。

三次多項式標準型如下： $$ \mathbf{f}(u) = \mathbf{a}_0 + \mathbf{a}_1u + \mathbf{a}_2u^2 + \mathbf{a}_3u^3 $$

使用標準型并不能直觀的描述曲綫，所以我們需要尋找一種替代方式，這種方式不僅要保證片段閒的連接性，還要保證片段閒的連續性。我們尋找的替代方式需要滿足一下四個屬性中任意三個（不會同時滿足四個）：

每個片段均爲三次多項式；
曲綫對控制點插值；
曲綫具有局部性；
曲綫滿足$C^2$連續。

注意，這裏所説的連續性是指片段之間、即節點位置的連續性。

在本章節之後提到的幾種樣條曲綫中，B-樣條曲綫不能對其控制點插值，但是其具有局部性和$C^2$連續性；Cardinal樣條曲綫和Catmull-Rom樣條曲綫雖然能對其控制點插值，并且具有局部性，但非$C^2$連續；Natural三次樣條曲綫不具有局部性。

15.5.1 Natural Cubics

自然三次樣條曲綫需要通過每個片段的端點，和起點位置的一階導數和二階導數來進行參數化。

$$ \begin{array}{l} \mathbf{p}_0 &= \mathbf{f}(0) &= \mathbf{a}_0 + 0^1 \mathbf{a}_1 + \ \ \ \ \ 0^2\mathbf{a}_2 + \ \ \ \ \ 0^3\mathbf{a}_3 \\[2ex] \mathbf{p}_1 &= \mathbf{f}'(0) &= \ \ \ \ \ \ \ \ \ 1^1\mathbf{a}_1 + 2\ \ \ 0^1\mathbf{a}_2 + 3 \ \ \ 0^2\mathbf{a}_3\\[2ex] \mathbf{p}_2 &= \mathbf{f}''(0) &= \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\ \ \ 1^1\mathbf{a}_2 + 6 \ \ \ 0^1\mathbf{a}_3\\[2ex] \mathbf{p}_3 &= \mathbf{f}(1) &= \mathbf{a}_0 + 1^1\mathbf{a}_1 + \ \ \ \ \ \ 1^2\mathbf{a}_2 + \ \ \ \ \ 1^3 \mathbf{a}_3 \end{array} $$

約束矩陣為：

$$ \mathbf{C} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 1 & 1 & 1 & 1 \end{bmatrix} $$

基矩陣為：

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & .5 & 0\\ -1 & -1 & -.5 & 1 \end{bmatrix} $$

給定$n$個控制點，自然三次樣條有$n-1$條三次樣條片段。通過上面參數化過程可知，對於自然三次樣條其采用依賴策略進行連接，因此其并具有局部性。儅曲綫某段發生變化時，會影響整條曲綫，至少會讓發生變化位置之後的曲綫受到影響。另外，我們只能在曲綫起始指定導數，而之後的導數都是由此推導而來。

15.5.2 Hermite Cubics

在第15.3.4節已給出Hermite三次样条計算方式及它的約束矩陣、基矩陣。由於Hermite三次樣條使用了兩個端點位置和一階導數，所以其只能保證$C^1$連續性。給定$n$個控制點，Hermite三次樣條曲綫包含$\frac{n-2}{2}$個樣條片段。

15.5.3 Cardinal Cubics - 基數三次樣條

Cardinal三次樣條是$C^1$連續的插值樣條。給定$n$個控制點，可獲得$n-2$個三次樣條片段。

基數三次樣條中，有一個參數$t$被稱爲"張量“係數，它用於控制著點之間的”鬆緊“程度。該參數取值為$[0, 1)$，儅$t = 0$時獲得的三次樣條曲綫稱爲Catmull-Rom樣條。

如下圖所示，每個基數三次樣條片段都會用到4個控制點，假設為$i$、$i+1$、$i+2$和$i+3$。每個片段由第二個控制點$i+1$開始，第三個控制點$i+2$結束；片段起始位置導數由第$i$和$i+2$個點連接的方向決定；片段結束位置導數由第$i+1$和$i+3$個點連接方向決定。

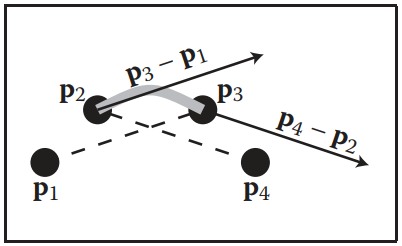
根據以上描述，我們可以寫出在鬆緊係數為$s = \frac{1-t}{2}$ 下三次樣條曲綫片段表示。

$$ \begin{array}{l} f(0) &= \mathbf{p}_2\\ f(1) &= \mathbf{p}_3\\ f'(0) &= \frac{1-t}{2}(\mathbf{p}_3-\mathbf{p}_1)\\ f'(1) &= \frac{1-t}{2}(\mathbf{p}_4-\mathbf{p}_2) \end{array} $$

整理可得：

$$ \begin{array}{l} \mathbf{p}_0 &= f(1) - \frac{1}{s}f'(0) &= \mathbf{a}_0 + (1 - \frac{1}{s})\ \ \ \mathbf{a}_1 + \ \ \ \ \ \ \ \ \mathbf{a}_2 + \ \ \ \ \ \ \ \ \ \mathbf{a}_3,\\ \mathbf{p}_1 &= f(0) &= \mathbf{a}_0,\\ \mathbf{p}_2 &= f(1) &= \mathbf{a}_0 + \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{a}_1 + \ \ \ \ \ \ \ \ \mathbf{a}_2 + \ \ \ \ \ \ \ \ \ \mathbf{a}_3,\\ \mathbf{p}_3 &= f(0) + \frac{1}{s}f'(1) &= \mathbf{a}_0 + \frac{1}{s} \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{a}_1 + 2\ \frac{1}{s}\ \ \mathbf{a}_2 + 3\ \ \frac{1}{s}\ \ \mathbf{a}_3 \end{array} $$

獲得基矩陣為：

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 0 & 1 & 0 & 0\\ -s & 0 & s & 0\\ 2s & s-3 & 3-2s & -s\\ -s & 2-s & s-2 & s \end{bmatrix} $$

基數三次樣條曲綫提供一種簡單的插值方式，并且提供$C^1$連續性和局部性，但由於只有$C^1$連續性，所以有時内部會出現"打結"現象。另外，鬆緊係數的不同也能夠控制曲綫，如下圖所示。

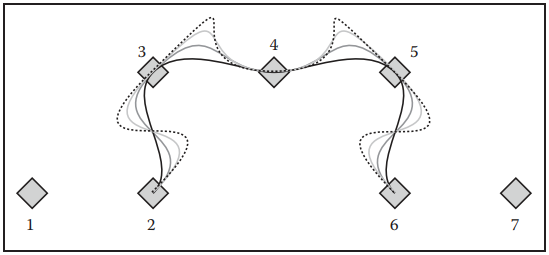
對比基數三次樣條和第15.3.6節提到的插值多項式，我們更傾向於選擇使用基數三次樣條，因爲插值多項式有以下幾個缺點：

插值多項式容易發生"overshoot”，而且隨著插值點數量增加，“overshoot"現象就越明顯；如下圖所示；
插值多項式的控制不具有局部性；
插值多項式的計算也不具有局部性，即需要使用所有點進行計算。

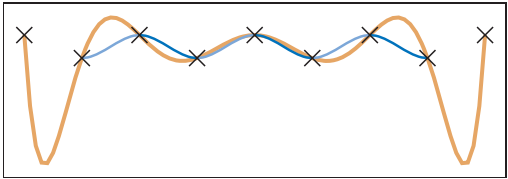
當然基數三次樣條也有缺點，首先就是在兩個端點出無法插值，但是這可以通過添加額外條件解決；另一個則是它只在節點位置提供了$C^1$連續。

15.6 Approximating Curves

用插值方式獲得曲綫的方式在實際中并不適用，它存在連續性不好、點於點之間如何連接不可控。所以，我們一般采用近似（擬合）的方式——控制點影響曲綫形狀，但不精確定義。圖形學中兩種最重要的近似方式是：$\mathrm{B\acute{e}zier}$曲綫和B-樣條曲綫。

15.6.1 $\mathrm{B\acute{e}zier}$曲綫

$\mathrm{B\acute{e}zier}$曲綫在圖形學中廣汎應用，它同樣也是多項式曲綫，通過$d+1$個控制點定義一條$d$次多項式曲綫。在圖形學中，一般使用三次($d = 3$)$\mathrm{B\acute{e}zier}$曲綫。

$\mathrm{B\acute{e}zier}$曲綫構造方式如下：

在曲綫首尾端點進行插值，即曲綫必經過$u = 0$和$u = 1$処的點；
曲綫首尾位置的一階導數由第一個二個控制點或倒數第一個和倒數第二個控制點構成的方向向量決定，曲綫的階數作爲方向向量的縮放係數；
若要表示首尾位置的$n$階導數，則需要用到起始或結尾$n+1$個點；

舉例，如下圖所示，一個三次貝塞爾曲綫，用$p_0$、$p_1$、$p_2$和$p_3$四個控制點表示，這樣我們就能得到：

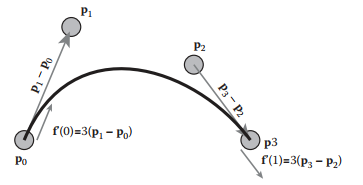
$$ \begin{array}{l} f(0) &= p_0\\ f(1) &= p_3\\ f'(0) &= 3(p_1 - p_0)\\ f'(1) &= 3(p_3 - p_2) \end{array} $$

由於之前説過，$\mathrm{B\acute{e}zier}$曲綫本質也是多項式曲綫，所以將本例中三次貝塞爾曲綫展開成多項式為：

$$ \begin{array}{l} p_0 &= f(0) &= a_30^3 + a_20^2 + a_10 + a_0\\ p_3 &= f(1) &= a_31^3 + a_21^2 + a_11 + a_0\\ 3(p_1 - p_0) &= f'(0) &= 3a_30^2 + 2a_20 + a_1\\ 3(p_3 - p_2) &= f'(1) &= 3a_31^2 + 2a_21 + a_1 \end{array} $$

求得其基矩陣為：

$$ \mathbf{B} = \mathbf{C}^{-1} = \begin{bmatrix} 1 & 0 & 0 & 0\\ -3 & 3 & 0 & 0\\ 3 & -6 & 3 & 0\\ -1 & 3 & -3 & 1 \end{bmatrix} $$

這樣我們就可以用混合函數形式寫出三次貝塞爾曲綫：

$$ \begin{align} f(u) &= (1-3u+3u^2-u^3)p_0 + (3u-6u^2 + 3u^3)p_1 + (3u^2 - 3u^3)p_2 + u^3p_3\\ \Leftrightarrow f(u) &= \sum_{i=0}^{d}b_{i,3}p_i \end{align}\tag{15.14} $$

其中：

$$ \begin{array}{l} b_{0,3} &= (1-u)^3\\ b_{1,3} &= 3u(1-u)^2\\ b_{2,3} &= 3u^2(1-u)\\ b_{3,3} &= u^3 \end{array} $$

仔細觀察可發現，$b_i$滿足Bernstein多項式展開形式：

$$ b_{k,n}(u) = C(n, k)u^k(1-u)^{(n-k)} $$

其中，$n$表示貝塞爾曲綫階數，$k$表示混合函數項數，$C(n,k)$為二次項係數，$C(n,k) = \frac{n!}{k!\ (n-k)!}$。

將這些帶入等式(15.14)中就可得到完整的三次貝塞爾曲綫混合函數表示。

$$ f(u) = \sum_{k=0}^{n}C(n,k)u^k(1-u)^{(n-k)}\ p_k $$

貝塞爾曲綫有幾個非常棒的性質：

貝塞爾曲綫能夠被由控制點構成的凸包完全包圍；
儅一條直綫與貝塞爾曲綫相交，交點個數不會多於該直綫與控制點按序相連直綫交點的個數；該特性稱爲Variation diminishing property（不知道中文怎麽說）；可參見下圖；

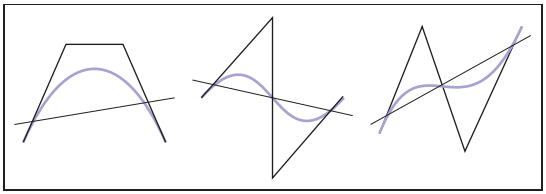
對稱性，將控制點順序翻轉，獲得的貝塞爾曲綫不變；
仿射不變性，平移、縮放、旋轉或斜切控制點與直接作用曲綫效果是一樣的；
計算和拆分貝塞爾曲綫的算法都足夠簡單有效。

上面説了單條貝塞爾曲綫如何表示，那儅將一組貝塞爾曲綫連接成完整一條曲綫時，需要通過共享端點來保證連續性（若只是這樣，只保證了$C^0$連續），不僅如此，在導數上也需要滿足一定條件，例如，對於$G^1$（$G$表示幾何連續），在連接位置，第一條曲綫的倒數第一個（共享點）和倒數第二個控制點必須與第二條曲綫第二個控制點共綫；對於$C^1$連續，不僅要滿足共綫，同時兩個向量長度還必須一樣，如下圖所示。對於高階連續性以此類推。

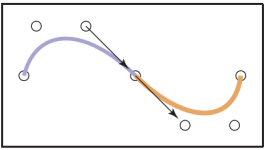
Geometric Intuition for $\mathrm{B\acute{e}zier}$ Curves

以上都是從代數方面推導了貝塞爾曲綫表示，下面從幾何角度對貝塞爾曲綫進行描述。

假設有一組控制點（數量較少），我們需要用這組控制點構造一條光滑的曲綫，最簡單的做法是將這組控制點用直綫按序連接，這樣獲得的曲綫并不光滑；爲了使其光滑，我們取已有綫段的中點，將相鄰中點連接，原綫段的一個端點移動到新綫段的中點，之後以這種方式不停迭代下去，最終就能獲得一條光滑的曲綫。整個過程如下圖所示。這種方式獲得的曲綫是$C^1$連續的。

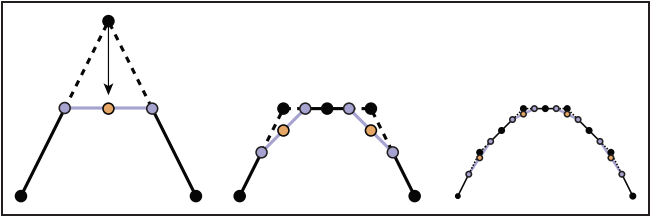
我們用代數方式描述該幾何處理過程，假設有三個點$(p_0, p_1, p_2)$，那麽在迭代第一次獲得的點$p_2'$為：

$$ p_2' = \frac{1}{2}(\frac{1}{2}p_0 + \frac{1}{2}p_1) + \frac{1}{2}(\frac{1}{2}p_1 + \frac{1}{2}p_2) $$

因爲我們這裏是以中點爲例，那麽將其改爲綫段任意比例位置，即$0 \leq u \leq 1$，我們可以類推得到：

$$ p(u) = (1-u)((1-u)p_0 + up_1) + u((1-u)p_1 + up_2) $$

重新整理後就可發現，這個就是二次貝塞爾曲綫的代數表示： $$ B_2(u) = (1-u)^2p_0 + 2u(1-u)p_1 + u^2p_2 $$

The de Casteljau Algorithm

根據上面幾何描述可知，貝塞爾曲綫可以利用一個遞歸的過程來表示，那麽在算法上同樣是利用該方式繪製任意數量控制點表示的曲綫。該算法被稱爲 de Casteljau algorithm。該算法過程的幾何表示如下圖所示。

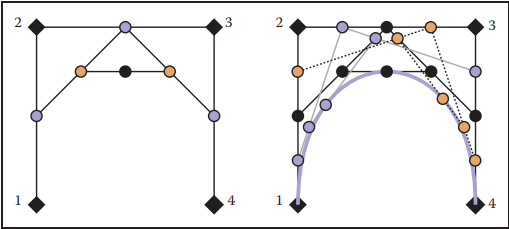
僞代碼如下：

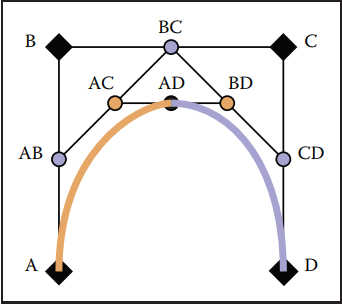
de Casterljau算法不僅用於繪製，還可以對貝塞爾曲綫進行拆分，用該算法計算過程中的結果點都可以作爲新的控制點，從而達到對曲綫拆分的目的，例如下圖中的AD點，形成新的兩條曲綫的控制點分別是A、AB、AC、AD和AD、BD、CD、D。

15.6.2 B-Splines

B-樣條可以利用$n$個控制點定義一條$d$次多項式曲綫，該曲綫具有$C^{(d-1)}$連續性。本節將使用B-樣條基函數的綫性組合來描述一條曲綫，這些基函數本身也是樣條曲綫，我們稱它為基樣條或B-樣條。注意，術語“B-樣條”是單指綫性組合中一個基函數，而非綫性組合后的函數，但是在圖形學中並不做這樣的區分，通常就用B-樣條指代綫性組合后的曲綫函數。

由其他函數綫性組合得到的新函數可表示爲： $$ f(t) = \sum_{i=1}^{n}p_ib_i(t)\tag{15.15} $$

其中，$p_i$表示係數，$b_i$表示基函數。使用該方式的關鍵在於，如何選取合適的$b_i$。

定義一組係數個數為$n$，參數為$k$的B-樣條，其中$k$比構成B-樣條的多項式次數多$1$（$k = d+1$）。那麽對於一個由$n$個點組成的參數為$k$的B-樣條具有：

$C^{(k-2)}$連續性；
構成其的多項式次數為$k-1$；
具有局部性 —— 任意位置僅依賴$k$個控制點；
被控制點構成的凸包包圍；
具有variation diminishing特性。

通過B-樣條創建曲綫不需要對其控制點進行插值。

Uniform Linear B-Splines

先看第一個均匀綫性B-樣條，其基函數如下:

$$ b_{i,2}(t) = \begin{cases} t - i, & if\ i\leq t < i + 1, \\ 2 - t + i, & if\ i+1 \leq t \leq i+2 \\ 0, & otherwise. \end{cases} \tag{15.16} $$

基函數圖像如下：

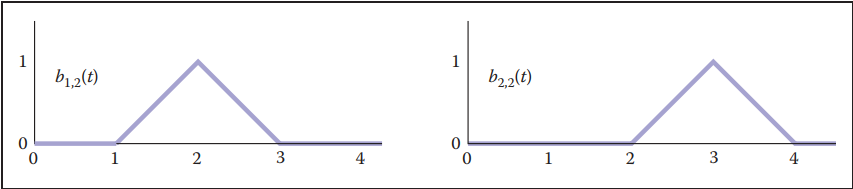
這裏用$b_{i, k}$表示某一個B-樣條基函數，其中$k = d + 1 = 2$表示綫性B-樣條。通過等式(15.15)的方式就能定義一個完整的曲綫函數。

對等式(15.16)進行實例化，使用$k$表示B-樣條曲綫階數，$n$表示用於組合的B-樣條數量。取$n = 4$、$i = 1$、$k = 2$，再將這些B-樣條畫在同一個坐標中，如下圖：

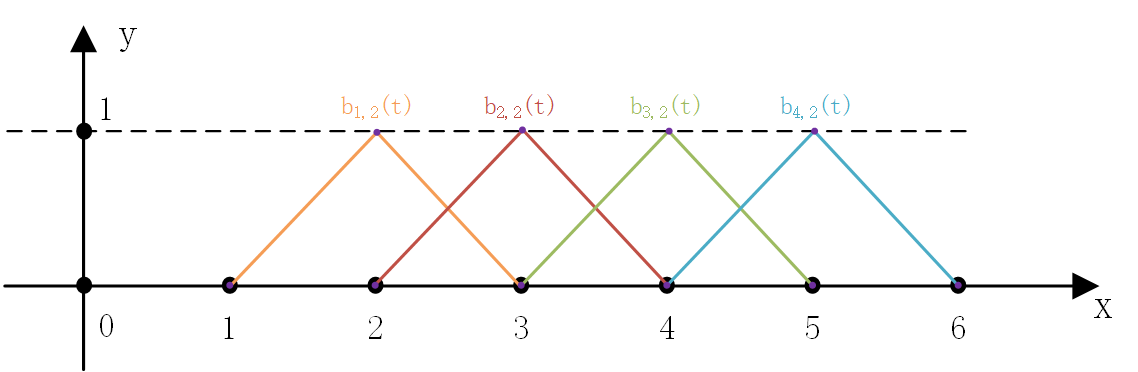
通過這個簡單的例子，可以總結幾個B-樣條的性質：

每一個B-樣條都有$k+1$個節點；
每一個B-樣條在第一個節點前和最後一個節點后都爲$0$值；
整個樣條曲綫具有局部性，因爲每個係數只和一個B-樣條函數相乘，并且這個B-樣條只在$k+1$個節點閒取非零值；
整個樣條曲綫有$n+k$個節點；
每一個B-樣條是$C^{(k-2)}$連續的，因此整個樣條曲綫也是$C^{(k-2)}$連續；
一組B-樣條中，從節點第$k$至第$n+1$個節點閒所有B-樣條的參數之和為$1$。這意味著B-樣條具有平移不變性：對控制點進行平移變換就相當於對整條曲綫做平移變換；
每兩個節點閒，B-樣條是一個$d = k-1$次多項式，因此，整條曲綫在任意兩個相鄰節點閒也可以用一個$d = k - 1$次多項式表示。

Uniform Quadratic B-Splines

下面討論$k = 3$的B-樣條曲綫，即均匀二次樣條曲綫。它是由三個二次多項式片段組成（四個節點），具有$C^1$連續性。它的數學表示如下：

$$ b_{i,3}(t) = \begin{cases} \frac{1}{2}u^2, & if \ \ i \leq t < i + 1;\ \ u = t- i\\ -u^2 + u + \frac{1}{2}, & if \ \ i+1 \leq t < i+2; \ \ u = t-(i+1)\\ \frac{1}{2}(1-u)^2, & if\ \ i+2 \leq t < i+ 3; \ \ u = t- (i+2)\\ 0, & otherwise. \end{cases}\tag{15.17} $$

下圖為$i = 2$時，均匀二次B-樣條曲綫圖形；

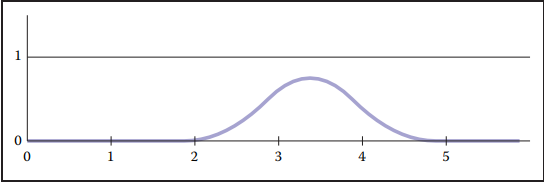
上節中總結出的B-樣條性質，也可以通過均匀二次B-樣條曲綫進行驗證。同樣，我們也可以寫出它的混合函數形式：

$$ f(u) = \frac{1}{2}(1-u)^2p_i + (-u^2 + u + \frac{1}{2})p_{i+1} + \frac{1}{2}u^2p_{i+2} $$

其中，$u = t - i$。

Uniform Cubic B-Splines

由於三次多項式在圖形學中非常重要，所以由它構成的B-樣條曲綫也非常值得討論。此時該B-樣條曲綫$k = 4$，完整曲綫由四段三次多項式曲綫組成，每段數學表示為：

$$ b_{i, 4}(t) = \begin{cases} \frac{1}{6}u^3, & \ if\ \ i \leq t < i+1; \ u = t - i\\[2ex] \frac{1}{6}(-3u^3 + 3u^2 + 3u + 1), & \ if \ \ i+1 \leq t < i+ 2; \ u = t - (i+ 1)\\[2ex] \frac{1}{6}(3u^3 - 6u^2 + 4), & \ if \ \ i+2 \leq t < i+ 3, \ u = t - (i+2)\\[2ex] \frac{1}{6}(-u^3 + 3u^2 - 3u + 1), & \ if \ \ i+3\leq t < i+4, \ u = t-(i+3)\\[2ex] 0, & otherwise. \end{cases}\tag{15.18} $$

儅$i = 1$時，其圖形如下：

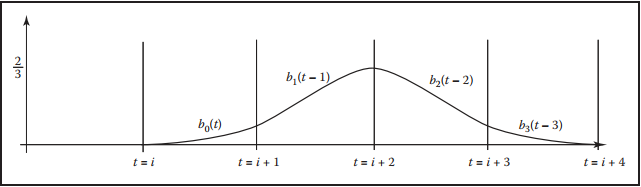
其混合函數可表示為：

$$ f(u) = \frac{1}{6}(-u^3 + 3u^2 -3u + 1)p_i + \frac{1}{6}(3u^3 - 6u^2 + 4)p_{i+1} + \frac{1}{6}(-3u^3 + 3u^2 + 3u+1) p_{i+2} + \frac{1}{6}u^3p_{i+3} $$

與15.5節中從約束矩陣中獲得基矩陣不同的是，其基矩陣可以從該混合函數多項式中推導出。

$$ \mathbf{M}_{b} = \frac{1}{6} \begin{bmatrix} -1 & 3 & -3 & 1\\ 3 & -6 & 3 & 0 \\ -3 & 0 & 3 & 0 \\ 1 & 4 & 1 & 0 \end{bmatrix} $$

15.6.3 Nonuniform B-Splines

B-樣條具有可以構建任意階曲綫的優秀性質($k > 1$)，所以當我們想要獲得更光滑曲綫時，增加$k$值是一個直接的手段，例如下圖中展示的。

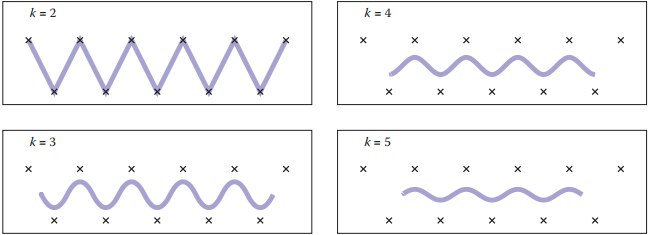
B-樣條不僅僅能汎化到$k>1$和$n \geq d$情況下，而且對於任意非減節點向量都可以。下面我們也將粗略介紹。

對於給定$n$和$k$，一組B-樣條曲綫（綫性組合）有$n + k$個節點，我們將這些節點用向量形式表示為$t$，對於均匀B-樣條，其節點向量為$\mathbf{t} = \begin{bmatrix}1, & 2, & 3, & \cdots, & n+k \end{bmatrix}$，我們可以將該節點向量汎化為滿足以下特點的非均匀形式：長度為$n + k$；任意元素$t_{i+1} \geq t_i$。這樣形成的非均匀節點空間有兩個好處：第一，能夠控制每個係數對整個函數的影響範圍；第二，允許使用重複點，使其得到特殊的性質。

舉個例子説明爲什麽非均匀形式能夠具有局部性。假設有$n = 4$的綫性($k = 2$)B-樣條，其均匀分佈的節點向量為$\mathbf{t} = [1, 2, 3, 4, 5, 6]$，根據15.6.2節給出的圖像可以知，在$t = 2$和$t = 5$之間，曲綫是由四個節點控制獲得，而在$1 \leq t \leq2$與$ 5 \leq t \leq 6$，則是由控制點直接插值得到。這樣，當我們想要在這個向量中插入一個點時（比如中點），均匀節點空間就必須延長空間長度，節點向量就更新為$\mathbf{t} = [1, 2, 3, 4, 5, 6, 7]$，這樣導致曲綫最後插值的點發生變化，這就得到與之前不一樣的結果；若使用非均匀節點空間，那麽其節點向量為$\mathbf{t} = [1, 2, 3, 3.5, 4, 5, 6]$，這樣對於曲綫末端并未產生影響。這就是非均匀B-樣條曲綫局部性的一個具體表現。

下面定義一般性的B-樣條，給定係數個數為$n$，B-樣條參數個數為$k$，節點向量為$t$（其長度為$n+k$），則通過遞歸等式可以定義出B-樣條：

$$ \begin{align} b_{i,1,t}(t) &= \begin{cases} 1 & \ if\ \ t_i \leq t < t_{i+1},\\ 0 & \ otherwise. \end{cases} \tag{15.19}\\[2ex] b_{i,k,t}(t) &= \frac{t-t_i}{t_{i+k-1} - t_i}b_{i,k-1}(t) + \frac{t_{i+k} - t}{t_{i+k} - t_{i+1}}b_{i+1, k-1}(t). \tag{15.20} \end{align} $$

該遞歸等式被稱為Cox-de Boor遞歸等式。之前的等式(15.17)和等式(15.18)也能通過這個方式推導得到。

Repeated Knots and B-Spline Interpolation

B-樣條曲綫有很多優秀的性質，但如果我們要在某個點上進行插值，對於之前介紹的B-樣條實現起來並不方便；有了非均匀B-樣條，我們可以通過重複點的方式對特殊點進行插值，例如下圖所示：

而重複點帶來的代價是損失了B-樣條的平滑性，以及總體函數表示。而對於曲綫端點，連續性并不是問題，這就使得重複點插值可以作用於曲綫端點。例如下圖，就采用了端點插值二次B-樣條曲綫。

對比之前給出的均匀二次B-樣條曲綫的圖像可知，在首尾位置的曲綫是不同的，對於重複點的圖像呈現非周期性。

15.6.5 NURBS

B-樣條曲綫優點很多，但依然會有一些曲綫是它無法表示的，例如圓錐曲綫。爲了彌補這一缺點，大神們又發明了有理非均匀B-樣條曲綫（NURBS），它將兩個非均匀B-樣條分別作爲分子和分母，用它們組合結果作爲曲綫的表示函數。 $$ f(u) = \frac{\sum_{i=1}^{n}h_ip_ib_{i,k,t}}{\sum_{i=1}^{n}h_ib_{i,k,t}} $$

其中，$h_i$表示權重因子，$p_i$表示控制點，$b_{i,k,t}$表示參數為$k$，節點向量為$t$的B-樣條。

NURBS除了具有B-樣條的很多有用性質外，還提供了令人驚奇的多種功能，因此在幾何建模中，被廣汎用於曲綫和曲面的表示。

15.7 Summary

對於本章做個總結。本章中討論了許多自由形式的曲綫表示，而對於圖形學來説，最重要的是下面幾種：

基數樣條曲綫：它通過對三次多項式進行插值獲得。
貝塞爾曲綫：用擬合控制點的方式獲得曲綫，有良好的性質和穩定的算法，在圖形學中廣汎應用；
B-樣條曲綫：對一系列B-樣條函數進行綫性組合，從而獲得曲綫，它通常用於獲得非常光滑的曲綫中。

參考資料

[1] Piegl, L., & Tiller, W. (1997). The NURBS book. Choice Reviews Online, 35(02), 35-0952-35–0952. https://doi.org/10.5860/CHOICE.35-0952

Author L1Mat2X

LastMod 2021-11-17

License CC BY-NC-ND 4.0

圖形學系列 Ch15-Curves-閲讀筆記

Contents