在第十八章中介紹了BRDF，它描述了光綫經過反射表面作用后的變化。在本章中，繼續討論某種材料對於視覺上最重要的屬性，並介紹一些有助於捕捉這些屬性的簡單模型。圖形學中大量使用了BRDF模型，本章介紹的模型是爲了給出非漫反射BRDF的概念。

Real-World Materials

現實中，許多材質在一定的視距下能夠清晰的看到它們的結構，比如地毯等；但是這些結構在本章中并不是所謂的材質屬性的組成部分，而是作爲幾何模型的組成部分。本章我們研究的結構是在正常視距下無法觀察到，但是它的確決定了宏觀上材料的外觀，它是材料屬性的一部分。最直觀的例子就是紙張上的纖維。這種劃分雖然武斷但在實踐中卻非常有效。

本節將定義幾類材質，并在之後反射模型中將這幾類材質作爲構建目標。

Smooth Dielectrics and Metals - 光滑絕緣體和金屬

這裏定義絕緣材質為能夠折射光的透明材質，比如玻璃等；在第十三章（PS：書中是説第四章，然後第四章并沒有提到）對於這種材質折射光綫的基本特性做了一定描述。而金屬材質能夠反射和像絕緣體材質一樣折射光綫，但是它能非常快速的吸收光綫，所以非常非常薄的金屬片就幾乎透明的。上面説了絕緣體和金屬材質，現在再介紹光滑材質，它只有兩個重要特性：

  1. 不同的入射角和波長的光有多少被反射？
  2. 光在穿透材質時，若給定距離和波長，它被吸收的比例是多少？

根據能量守恆定律，折射光能量等於未被反射的光的能量。對於金屬材質，我們假設他們會被立即吸收；而對於絕緣體材質，根據Beer's Law能量損失與進入材質的距離成正比。

對於反射光，根據Fresnel equations，隨著入射角的增大，反射光能量增大，特別是接近掠射角時。

上面描述的反射、折射光特性都能在下面兩張圖中表示。

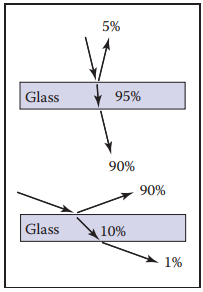
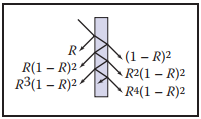
上面右圖表示了光綫在材質中做了多次反射和折射，但實際中，大多數時候只有前一到兩次的反射才容易被看見。

Rough Surfaces - 粗糙表面

如果金屬或絕緣體有輕微程度的粗糙化，但又不足以讓光發生衍射，我們就可以把這個表面當作是微表面microfacet。microfacet，Wiki中的解釋是This can be explained by the existence of microfacets. We assume that surfaces that are not perfectly smooth are composed of many very tiny facets, each of which is a perfect specular reflector.這種表面的特性就是在近距離下表現出鏡面反射，但在遠距離時，光會以一定分佈發生散射。代表材料有拉絲金屬表面、鋁箔紙的霧面等。

對於絕緣體材質，比如玻璃，儅其表面有細微不規則表面結構時，它會表現出一定模糊的效果，但是我們依舊能透過它看清物體。儅這種表面結構不規則程度加深時，我們認爲它是半透明而不是透明的。

這種材質也可稱爲Glossy材質，其模型和效果如下圖所示。

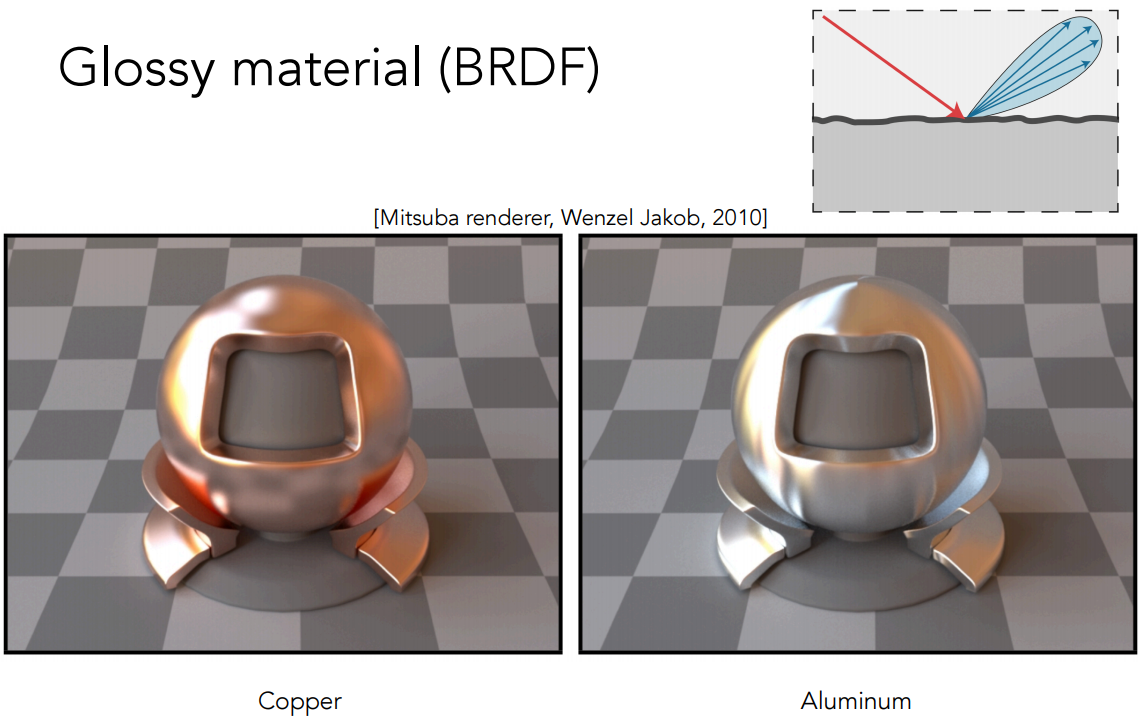
Diffuse Materials - 漫反射材質

如果說一個材質是漫反射的，那麽就表示該材質不光滑、沒有光澤。我們常見的一些物體就屬於這種材質，例如紙、石頭、未抛光過的木頭等。利用常量Lambertian BRDF就能夠簡單近似漫反射材質表面。但是，真是的漫反射材質在一定的入射角（接近掠射角）下會表現出一定程度的鏡面反射效果。該材質效果如下圖所示。

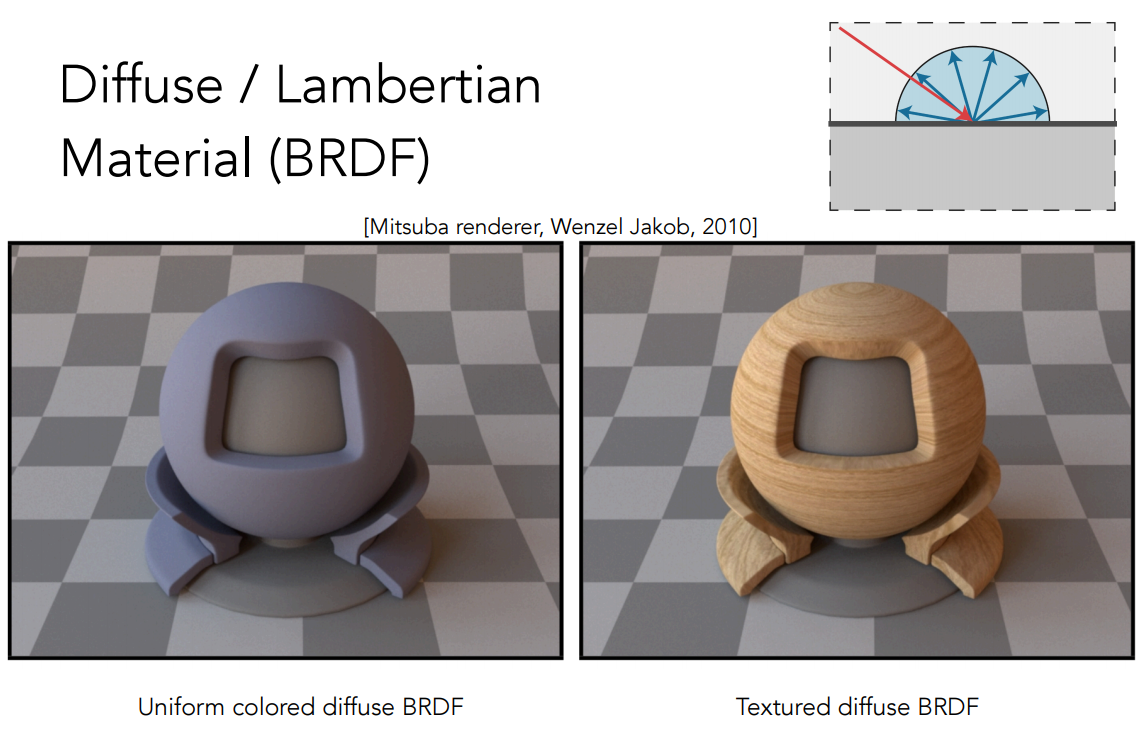
Translucent Materials - 半透明材質

對於薄物體，例如樹葉和紙片，它會對透射光和反射光產生散射效果。在實際情況下，透過這種材質很難獲得清晰的圖像；另外這種材質會使光在色調上發生偏移。比如，紅色的紙張呈現出紅色（反射光），這是因爲光在透入紙内一個很短距離時，非紅光的光被濾除，然後紅光被散射回來。透過紅紙看到的也是紅色這一現象也可以用這個原理解釋。這一屬性的一個暗示是，傳播係數在兩個方向上必須一致。（PS: 不理解什麽意思）

Layered Materials

還有一些材質是由“一層層”同材質構成的，例如光滑絕緣體材質敷在顆粒材質表面，以此來獲得漫反射特性。如下圖所示。

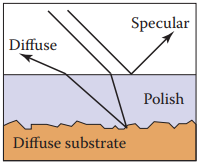
圖中，光在絕緣層表面發生鏡面反射，并且有一部分光透射進絕緣層，透射進的光要麽被吸收，要麽經過漫反射材質表面反射會絕緣層表面，此時有些光會繼續發生透射，有些則無法透射。這些反射光、透射光等一起構成了“反射”成分。

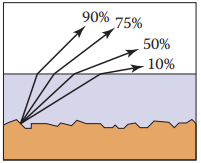
注意，從漫反射材質反射囘絕緣體表面的光，在發生透射時依舊要滿足Fresnel等式，這就説明BRDF就不能是一個常量，而應該在掠射角附近突然消失的一個量。如下圖所示。

figure 24.4

Implementing Reflection Models

利用BRDF進行渲染能夠獲得比較好的效果，但是它本身是非常複雜的，很難從原理推導出。但是，通過實驗的方式，我們可以獲得近似結果。下面就來討論BRDF這種近似模型。

首先，BRDF模型需要滿足物理約束，一個是能量守恆，即： $$ \text{for all }k_i, R(k_i) = \int_{all\ k_o}\rho(k_i, k_o)\cos{\theta_o}\ d\sigma_o \leq 1 $$

另一個是可逆性，即： $$ \text{for all }k_i, k_o, \rho(k_i, k_o) = \rho(k_o, k_i) $$

接著，BRDF模型能夠清晰的區分漫反射項和鏡面反射項。

第三，模型擁有直觀的參數。比如Phong模型爲什麽如此"長壽“，是因爲模型中漫反射常數和指數都直觀的與表面性質相關，一個與表面顔色相關，另一個與高亮區域大小相關。

最後，也是該模型能夠工程化的重要性質，就是能夠利用蒙特卡洛積分進行采樣。回顧蒙特卡洛積分和方向為$k_o$的傳輸方程：

$$ \int f(x)d\mu \approx \frac{1}{N}\sum_{j=1}^{N}\frac{f(x_j)}{p(x_j)}\\[2ex] L_s(k_o) = \int_{all\ k_i}\rho(k_i, k_o) L_f(k_i) \cos{\theta_i}\ d\sigma_i $$

利用第二十三章討論的pdf$p(k_i)$對方向進行采樣，這樣就可以利用采樣來近似表面輻射率：

$$ L_s(k_o) \approx \frac{1}{N}\sum_{j=1}^{N}\frac{\rho(k_j,k_o)L_f(k_j)\cos{\theta_j}}{p(k_j)} $$

只要被積函數非零処$p(k)$取值非零，則上式就能收斂。爲了獲得好的近似效果，$p(k)$在形狀上最好能與$\rho(k_i, k_o)L_f(k_i)\cos{\theta_i}$一致，但現實中很難實現，所以最好的選擇是讓$p(k)$的形狀在某種程度上相似于$\rho(k_i, k_o)L_f(k_i)\cos{\theta_i}$。

最後一個特點是，相同的BRDF模型能有很多可接受的pdf，即$p(k_i)$不唯一。

Specular Reflection Models

對於金屬，假設其標準反射率為$R_0(\lambda)$，根據Fresnel等式可知，隨著入射角的增大，其反射率是在發生變化的。由於Fresnel等式比較複雜，所以一般用Schlick近似：

$$ R(\theta, \lambda) = R_0(\lambda) + (1 - R_0(\lambda))(1 - \cos{\theta)})^5 $$

這種近似就可以通過數據或目測來設置標準反射率$R_0$即可。

對於絕緣體， 該近似等式同樣成立，但是對於標準反射率則需要通過下面式子獲得。 $$ R_0(\lambda) = \left(\frac{n(\lambda) - 1}{n(\lambda) + 1}\right)^2 $$

一般情況下， 物體折射率$n$不會隨著波長$\lambda$變化而變化，但在散射場景下，$n$是可變的。常用的物體折射率有水($n = 1.33$)，玻璃($n = 1.4 \sim 1.7$)，鑽石($n = 2.4$)。

Smooth-Layered Model

無論是啞光材質或是鏡面材質，其反射受表面Fresnel等式和亞表面散射控制。這種模型的一個例子如下圖所示。

figure 24.5

這種現象的解釋原文完全沒看懂，貼在這裏等以後再説吧~

Note that the blurring in the specular reflection is mostly vertical due to the compression of apparent bump spacing in the view direction. This effect causes the vertically streaked reflections seen on lakes on windy days; it can either be modeled using explicit microgeometry and a simple smooth-surface reflection model or by a more general model that accounts for this asymmetry.

雖然解釋看不懂，但不影響後續模型推導。對於圖片中的瓷磚，采用傳統Lambertian反射模型，即綫性的叠加反射項和Lambertian項。用標準輻射度量學可表示爲：

$$ \rho(\theta, \phi, \theta^{'}, \phi^{'}, \lambda) = \frac{R_d(\lambda)}{\pi} + R_s\rho_s(\theta, \phi, \theta^{'}, \phi^{'}) \tag{24.1} $$

其中，$R_d(\lambda)$表示啞光項的半球反射率，$R_s$表示鏡面反射率，$\rho_s$表示歸一化後的BRDF項。該簡化模型中$R_s$獨立於波長$\lambda$。波長獨立性引起與光源顔色一致的高光區，這樣就獲得類似抛光的效果而不是金屬效果。

爲了保證能量守恆，通常會設定$R_d(\lambda) + R_s \leq 1$。該簡化模型中，若固定$R_s$，則隨著觀測角度變得陡峭，而不會增加鏡面反射。而在真實世界中，啞光項和高光項的相對比例會隨著觀測角度變化而變化。

爲了達到這個目的，將等式(24.1)修改為如下形式：

$$ \rho(\theta, \phi, \theta^{'}, \phi^{'}, \lambda) = R_f(\theta)\rho_s(\theta, \phi, \theta^{'}, \phi^{'}) + \frac{R_d(\lambda)(1-R_f(\theta))}{\pi} \tag{24.2} $$

其中，$R_f(\theta)$為空氣中抛光表面的菲涅爾反射率。

等式(24.2)最大的一個問題是——不互逆。若交換$\theta$和$\theta^{'}$，啞光阻尼係數則會隨著$(1-R_f(\theta))$的變化而發生改變。

下面介紹一個耦合模型，它耦合了啞光係數和鏡面反射係數，但它能夠保證互逆性和能量守恆。下面詳細分析下分層模型中光的傳播，以此推導出新模型的改進方向。

對於擁有光澤(glossy)特徵的表面，通常是光亮的絕緣體，例如油或聚氨酯等，它們都有某種亞表面結構。其中，反射過程中的鏡面反射分量通常是由光滑表面引起，並獨立於該光滑表面下的結構，而且鏡面反射分量的大小受控于菲涅爾公式。再來看看非鏡面反射部分的光發生了什麽。這部分光透過該表面，要麽被亞表面吸收，要麽通過亞表面反射后穿過原先光滑的表面。這部分光就構成了啞光分量。由於啞光分量只包含從亞表面反射囘的透射光，因此伴隨著角度增加，總能量自然會發生減少。

由於等式(24.1)中，鏡面反射分量$R_f(\theta)$是直接從絕緣體-空氣界面的物理特性中推導而來。因此最終問題就落在啞光分量上。通過模擬技術理論上可以像鏡面反射分量獲得啞光分量，但這樣不僅代價高昂，而且需要對亞表面結構有詳細瞭解，但亞表面結構通常有許多未知和難以測量的量。這樣，將啞光項修改爲一個簡單的逼近項，以此來獲得圖24.4的角度特性。

根據上面的描述，開始對模型中啞光項進行修改，以達到簡化並符合物理性質的目的。首先假設，啞光項為非Lambertian的，用依賴$\theta$、$\theta^{'}$和$\lambda$的項：$\rho_m(\theta, \theta^{'}, \lambda)$代替。這裏我們忽略了$\phi$和$\phi^{'}$變量，是因爲真實中的啞光項非常複雜且有時需要考慮位置因素，而這麽簡化是爲了讓模型更簡單，并且希望啞光項能接近一個常數，同時大致滿足旋轉對稱性。

爲了保證互逆性，將$\rho_m(\theta, \theta^{'}, \lambda)$改寫成下面形式： $$ \rho_m(\theta, \theta^{'}, \lambda) = kR_m(\lambda)f(\theta)f(\theta^{'}) $$

這樣，我們將之前等式(24.1)表示的模型改寫下面這種可分離的形式： $$ \rho(\theta, \phi, \theta^{'}, \phi^{'}, \lambda) = R_f(\theta)\rho_s(\theta, \phi, \theta^{'}, \phi^{'}) + kR_m(\lambda)f(\theta)f(\theta^{'}) \tag{24.3} $$

其中，$R_m(\lambda)$取值範圍為$0\sim 1$。儅$R_m(\lambda)=1$，表示入射能量與反射能量相同，同時意味著對於任意入射角$\theta$和波長$\lambda$的BRDF需滿足下面的約束條件：(PS：沒理解這個約束條件的物理含義) $$ R_f(\theta) + 2\pi k f(\theta)\int_{0}^{\frac{\pi}{2}}f(\theta^{'})\cos{(\theta^{'})}\sin{(\theta^{'})}\mathrm{d}\theta^{'} = 1 \tag{24.4} $$

通過約束條件(24.4)可知，$f(\theta)$與$1-R_f(\theta)$成正比關係，這樣就能將等式(24.3)改寫爲： $$ \rho(\theta, \phi, \theta^{'}, \phi^{'}, \lambda) = R_f(\theta)\rho_s(\theta, \phi, \theta^{'}, \phi^{'}) + kR_m(\lambda)[1-R_f(\theta)][1-R_f(\theta^{'})] \tag{24.5} $$

等式(24.5)對於部分能量被吸收的啞光項也同樣適用。至此，等式(24.5)中，$R_f(\theta)$可通過菲涅爾等式獲得，現只剩$k$是沒有定義，但是我們可以通過能量守恆推導獲得。將$f(\theta) \propto (1-(1-\cos{(\theta)})^5)$以及$R_f(\theta) \approx R_0 + (1-\cos{(\theta)})^5(1-R_0)$帶入等式(24.4)解得： $$ k = \frac{21(1-R_0)}{20\pi}\tag{24.6} $$

這裏等式(24.6)與書中結果不同，而且在作者Peter Shirley1997年的兩篇論文[1][2]中也給出的結果也不相同，個人偏向于等式(24.6)形式，但是其中的係數與個人推導不一致！！！

至此，獲得完整的耦合BRDF模型的近似等式：

$$ \rho(\theta, \phi, \theta^{'}, \phi^{'}, \lambda) = [R_0 + (1-\cos{(\theta)})^5(1-R_0)]\rho_s(\theta, \phi, \theta^{'}, \phi^{'}) + kR_m(\lambda)[1-(1-\cos{\theta})^5][1-(1-\cos{\theta^{'}})^5] \tag{24.7} $$

圖24.5就是利用該耦合模型渲染得到的。

Rough-Layered Model

上面的耦合模型對於光滑表面的渲染效果很好，但是現實中的表面不一定都是光滑的，這些表面對於鏡面反射項有一定的散射作用，對於這種一般性的表面，可以總結一下幾個特徵：

  1. Plausible - BRDF模型需要滿足能量守恆以及互逆性；
  2. Anisotropy - 材質能夠對簡單的各向異性建模；
  3. Intuitive Parameters - 材質建模具有直觀的模型參數，例如表面粗糙度參數$n_u$和$n_v$；
  4. Fresnel behavior - 滿足菲涅爾特性；
  5. Non-Lambertian diffuse term - 材質允許有漫反射項，但該漫反射項是non-Lambertian的，因爲要滿足菲涅爾特性且要保證能量守恆；
  6. Monte Carlo friendliness - 能夠直接使用蒙特卡洛積分對BRDF模型進行采樣。

爲滿足這些特徵，基本策略是 to make a Fresnel-weighted Phong-style cosine lobe model that is anisotropic.參考公式(24.1)，這裏同樣將BRDF分爲兩部分：鏡面反射部分和漫反射部分。 $$ \rho(\mathbf{k}_1, \mathbf{k}_2) = \rho_s(\mathbf{k}_1, \mathbf{k}_2) + \rho_d(\mathbf{k}_1, \mathbf{k}_2)\tag{24.8} $$

其中，$\mathbf{k}_1$表示指向光源的單位向量，$\mathbf{k}_2$表示指向觀察者的單位向量。另外，定義$\mathbf{n}$表示法向量，$\mathbf{h}$表示$\mathbf{k}_1$和$\mathbf{k}_2$的half-verctor。

下面兩節將對公式(24.8)的兩部分分開介紹。 以下兩部分内容書中都沒詳細展開，好多地方個人看的有些懞，强烈建議直接看論文[3]，論文中將整個模型的推導過程寫的非常詳細。

Anisotropic specular BRDF

先對某一點的反射進行幾何建模，如下圖所示。

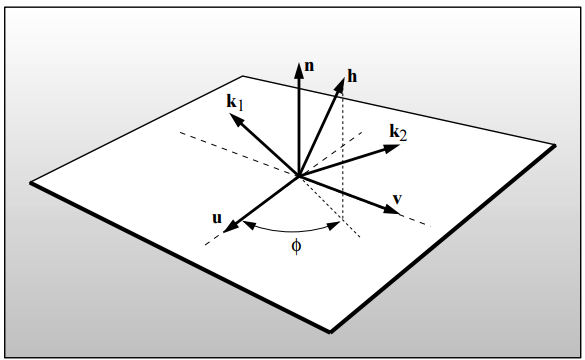
其中，各個項的含義如下圖所示。

這裏我們利用具有各向異性的Phong-style specular lobe模型作爲初始模型，並加入菲涅爾特性。其BRDF如下： $$ \rho(\mathbf{k}_1, \mathbf{k}_2) = \frac{\sqrt{(n_u+1)(n_v+1)}}{8\pi}\frac{(\mathbf{n}\cdot\mathbf{h})^{n_u\cos^2{\phi}+n_v\sin^2{\phi}}}{(\mathbf{h}\cdot\mathbf{k}_i)\max{(\cos{\theta_i}, \cos{\theta_o})}}F(\mathbf{k}_i\cdot \mathbf{h})\tag{24.9} $$

其中，$n_u$和$n_v$表示粗糙度。利用Schlick近似替換菲涅爾項可知： $$ F(\mathbf{k}\cdot \mathbf{h}) = R_s + (1-R_s)(1-(\mathbf{k}\cdot \mathbf{h}))^5 \tag{24.10} $$

這裏，$R_s$表示材質在空氣中的反射率。由於$\mathbf{k}_i\cdot \mathbf{h} =\mathbf{k}_o\cdot \mathbf{h}$，這滿足互逆性，這樣就得到了滿足能量守恆及互逆性的模型。等式(24.9)的推導過程及合理性論證可以參考論文[3]中第二節内容。

下圖展示了利用這個模型，在不同$n_u$和$n_v$下，金屬球的反射效果。

還是補充下論文[3]中對等式(24.9)的推導過程，有些地方不知理解是否正確，望指正。

首先，根據前人的研究並結合各項異性的特點，可以得到一個初始的BRDF模型為： $$ \rho(\mathbf{k}_1, \mathbf{k}_2) = c * \frac{(\mathbf{n}\mathbf{h})^{n_u\cos^2{\phi}+n_v\sin^2{\phi}}}{\max{(\mathbf{n}\mathbf{k}_1, \mathbf{n}\mathbf{k}_2)}} F(\cos{\theta})\tag{24.11} $$

接著，利用微表面microfacet模型，引入概率密度函數$p_h(\mathbf{h})$。 $$ p_h(\mathbf{h}) = \frac{\sqrt{(n_u+1)(n_v+1)}}{2\pi}(\mathbf{n}\mathbf{h})^{n_u\cos^2{\phi} + n_v\sin^2{\phi}}\tag{24.12} $$

根據能量守恆及半球反射率的定義（可參看第十八章内容），可知：

$$ R(\mathbf{k}_1) = \int_{\mathbf{k}_2}\rho(\mathbf{k}_1, \mathbf{k}_2)(\mathbf{k}_2 \cdot \mathbf{n}) \mathrm{d}\omega_{k_2} \leq 1 \tag{24.13} $$

將等式(24.11)帶入(24.13)中可得：

$$ c * \int_{\mathbf{k}_2}\frac{(\mathbf{n}\mathbf{h})^{n_u\cos^2{\phi}+n_v\sin^2{\phi}}}{\max{(\mathbf{n}\mathbf{k}_1, \mathbf{n}\mathbf{k}_2)}} F(\cos{\theta})(\mathbf{k}_2 \cdot \mathbf{n}) \mathrm{d}\omega_{k_2} \leq 1 \tag{24.14} $$

等式中，對於確定的$\mathbf{k}_1$，定有 $$ \frac{\mathbf{k}_2 \cdot \mathbf{n}}{\max{(\mathbf{n}\mathbf{k}_1, \mathbf{n}\mathbf{k}_2)}} \leq 1 $$

因此将该项忽略或用一个小于$1$的因子取代，得： $$ c^{'} * \int_{\mathbf{k}_2}p_h(\mathbf{h})F((\mathbf{k}\mathbf{h}))\mathrm{d}\omega_{k_2} \leq 1 \tag{24.15} $$

根據微表面呈鏡面反射的假設，反射光綫空間中的微分立體角與微表面法綫閒的關係如下[4]: $$ \mathrm{d}\omega_{k_2} = 4(\mathbf{k}_1\mathbf{h})\mathrm{d}\omega_h \tag{24.16} $$

利用(24.16)及$F \leq 1$（不懂這個條件怎來的），帶入(24.15)得： $$ c^{'} * \int_{\mathbf{h}}p_h(\mathbf{h})4(\mathbf{k}_1\mathbf{h})\mathrm{d}\omega_h \leq 1 \tag{24.17} $$

到這裏，所有的前置條件都給出了，我們最後是爲了得到各向異性且能量守恆的鏡面反射BRDF模型，其中概率密度函數$p_h(\mathbf{h})$在半球上的積分結果為$1$，那麽，我們令新的BRDF模型為$\frac{\rho(\mathbf{k}_1,\mathbf{k}_2)}{4(\mathbf{k}_1\mathbf{h}}$，另外$c^{'}$是一個常數係數，我們也令其取值為$1$，這樣，帶入(24.12)至(24.17)推導過程中就論證新的BRDF模型是滿足我們需求的，即等式(24.9)。

Diffuse Term for the Anisotropic Phong Model

對於漫反射項，如果使用Lambertian BRDF與各向異性鏡面反射項結合，會造成能量不守恆現象。先觀察下圖中的現象。

從圖中可以發現，隨著入射角度的增加，桌面的本身顔色是慢慢消失，即桌面的漫反射顔色慢慢消失。這樣對於漫反射項，更好的方式是采用簡單的角度依賴，因爲鏡面反射率隨著入射角的變化而變化，若總能量為$1$，那麽鏡面反射能量隨著角度變化而變化，爲了保證能量守恆，漫反射項也必須做出相應的變化。

這樣可得出耦合模型下漫反射項如下： $$ \rho_d(\mathbf{k}_1, \mathbf{k}_2) = \frac{28R_d}{23\pi}(1-R_s)\left(1 - \left(1- \frac{\cos{\theta_i}}{2}\right)^5\right)\left(1 - \left(1-\frac{\cos{\theta_o}}{2}\right)^5\right) \tag{24.18} $$

其中，$R_d$是空氣中介質的漫反射係數，$R_s$是Phong lobe係數。

Implementing the Model

到目前爲止，已將等式(24.8)拆分成鏡面反射項等式(24.10)和漫反射項等式(24.11)，它們計算時都需要用到三角函數，這在實際實現中是一個巨大的計算開銷，因此我們利用公式$\mathbf{a} \cdot \mathbf{b} = ||\mathbf{a}||\cdot||\mathbf{b}|| \cos{\phi}$及幾何關係對等式進行改寫。

其中，等式(24.10)改寫爲如下形式：(PS:這個等式改寫原書中可能有錯，這裏參考論文[3]中給出) $$ \rho(\mathbf{k}_1, \mathbf{k}_2) = \frac{\sqrt{(n_u+1)(n_v+1)}}{8\pi}\frac{(\mathbf{n}\cdot \mathbf{h})^{\frac{(n_u(\mathbf{h}\cdot\mathbf{u})^2 + n_v(\mathbf{h}\cdot\mathbf{v})^2)}{(1-(\mathbf{h}\mathbf{n})^2)}}}{(\mathbf{h}\cdot\mathbf{k})\max{((\mathbf{n}\cdot\mathbf{k_1}),(\mathbf{n}\cdot\mathbf{k_2}))}}F(\mathbf{k}\cdot \mathbf{h})\tag{24.19} $$

在蒙特卡洛積分中，我們關心的問題是，通過已知方向$\mathbf{k}_1$去生成$\mathbf{k}_2$方向的樣本，并且該樣本需要滿足近似cosing weighted BRDF的分佈。

我們已知等式(24.12)，這樣可以獲得$\mathbf{h}$的采樣。如果通過 $$ \mathbf{k}_o = -\mathbf{k}_i + 2(\mathbf{k}_i \cdot \mathbf{h})\mathbf{h} $$

去生成$\mathbf{k}_o$的采樣，其分佈并不是$p_h(\mathbf{k}_o)$的，這是因爲$\mathbf{h}$和$\mathbf{k}_o$的測量方式不同造成的，所以，為獲得理想的$\mathbf{k}_o$采樣，可通過如下形式計算得到： $$ p(\mathbf{k}_o) = \frac{p_h(\mathbf{h})}{4(\mathbf{k}_i\mathbf{h})} $$

因爲是采樣，所以肯定會出現采樣到的反射光方向位於表面下方，此時要把其權重設爲零，這也是能量損失的主要原因，但隨著$n_u$和$n_v$的變大，這個問題也變得不那麽明顯了。

最後還剩一個問題，就是如何利用等式(24.12)生成向量$\mathbf{h}$。生成$\mathbf{h}$的本質是要確定它的方位角$\phi$和極角$\theta$。先考慮$(\theta, \phi) \in [0,\frac{\pi}{2}] \times [0, \frac{\pi}{2}]$範圍内的情況（這是半球中的第一象限），定義兩個隨機變量$(\xi_1, \xi_2)$，它們服從$[0,1]$的均匀分佈。那麽： $$ \phi(\xi_1) = \arctan{\left(\sqrt{\frac{n_u + 1}{n_v + 1}}\tan{\left(\frac{\pi\xi_1}{2}\right)}\right)}\tag{24.20} $$

接著，根據下式利用$\phi$來獲得$\theta$：

$$ \cos{\theta}(\phi, \xi_2) = (1- \xi_2)^{1/(n_u\cos^2{\phi} + n_v\sin^2{\phi} + 1)}\tag{24.21} $$

至於整個球體的采樣，可以標準方式獲得，根據$\xi_1$所屬$[0,0.25),[0.25,0.5),[0.5,0.75), [0.75,1)$四個中的哪個，來選擇映射函數。然後按照坐標軸$\phi = \pi /2$對其進行翻轉，來獲得另外半球的結果。

對於漫反射項，可以采用更簡單的方式，例如利用餘弦分佈進行采樣，這樣十分接近于完全的漫反射BRDF，也相當大地減少了蒙特卡洛估計的方差。

Frequently Asked Questions

參考文獻

[1]. Shirley, P., Hu, H., Lafortune, E., & Blocksom, J. (1997). A coupled matte-specular reflection model. Submitted to Sigghraph, 97.

[2]. Shirley, P., Smits, B., Hu, H., & Lafortune, E. (1997). A practitioners’ assessment of light reflection models. Proceedings The Fifth Pacific Conference on Computer Graphics and Applications, 40–49.

[3]. Ashikhmin, M., & Shirley, P. (2000). An Anisotropic Phong BRDF Model. Journal of Graphics Tools, 5(2), 25–32.