論文《A General algorithm for computing distance transforms in linear time》閲讀筆記整理。

Introduction

距離變換本質是計算點到點的距離，如果在二維空間中，可以按如下方式描述。

假設$B$為尺寸為$m \times n$點的集合，那麽距離變換所計算的就是$B$中某點$(x,y)$到集合$B$中最近點的距離（就是前景點到最近背景點的距離）。若$B$用二值矩陣$b[:, :]$表示（標記圖），且距離為標準歐式距離，那麽每個點$(x,y)$的距離可以表示為： $$ dt[x,y] = \sqrt{EDT(x,y)} $$

其中，

$$ EDT(x,y) = \min{(i, j : 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : (x -i)^2 + (y-j)^2)} $$

解釋下$\min{(k:P(k):f(k))}$這種表示方式的含義：滿足函數$f(k)$最小值，且取值範圍在$P(k)$中的所有$k$的集合。

除了上面提到的歐式距離，還可以采用其他距離計算方式，例如曼哈頓距離(Manhattan distance)、棋盤距離(Chessboard distance)等。

$$ \begin{array}{l} MDT(x,y) &=& \min{(i, j: 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : |x-i| + |y -j|)}\\[2ex] CDT(x,y) &=& \min{(i,j: 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : \max(|x-i|, |y-j|))} \end{array} $$

本文就介紹在這三種距離函數下，如何在綫性時間内完成一幅圖像的距離變換，并且該算法可以并行計算。

現在先將上面三種距離計算函數進行轉換。

$$ \begin{array}{l} EDT(x,y) &=& \min{(i, j : 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : (x -i)^2 + G(i,y)^2)}\\[2ex] MDT(x,y) &=& \min{(i, j: 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : |x-i| + G(i,y))}\\[2ex] CDT(x,y) &=& \min{(i,j: 0 \leq i < m \wedge 0 \leq j < n \wedge b[i,j] : \max(|x-i|, G(i,y)))} \end{array} $$

其中，$G(i,y) = \min{(j : 0 \leq j < n \wedge b[i,j]: |y-j|)}$，很明顯，這麽做轉換在程序上就能將行列操作分離，這樣該算法的整理框架就可以描述為：第一次全圖按列遍歷，即取$C_x$（$x$為固定列號），計算$C_x$中每個點$(x, j), 0\leq j < n$與$C_x \wedge B$的最近距離$G(x,y)$。再進行第二次全圖遍歷，此時按行遍歷，此時再利用$EDT$、$MDT$或$CDT$計算每個點$(x,y)$的最終距離值。

下面按兩次遍歷分別説明。

The first phase

根據上面描述，第一階段就是計算$G(x,y)$，在細化$G(x,y)$可以把其分爲兩個階段：

$$ \begin{array}{l} GT(i,y) &=& \min{(j:0\leq j < y \wedge b[i,j] : y - j)} \\[2ex] GB(i,y) &=& \min{(j:y \leq j < n \wedge b[i,j] : j - y)} \end{array} $$

若$b[i,y]$被標記，則$GT(i,y) = 0$(PS：這裏與個人理解是相反的，個人理解是$b[i,y]$未被標記，$GT(i,y) = 0$)；其他情況$GT(i,y) = GT(i, y-1)+1$。而$GB(i,y) = GB(i,y+1) + 1$。可以參考下圖理解。

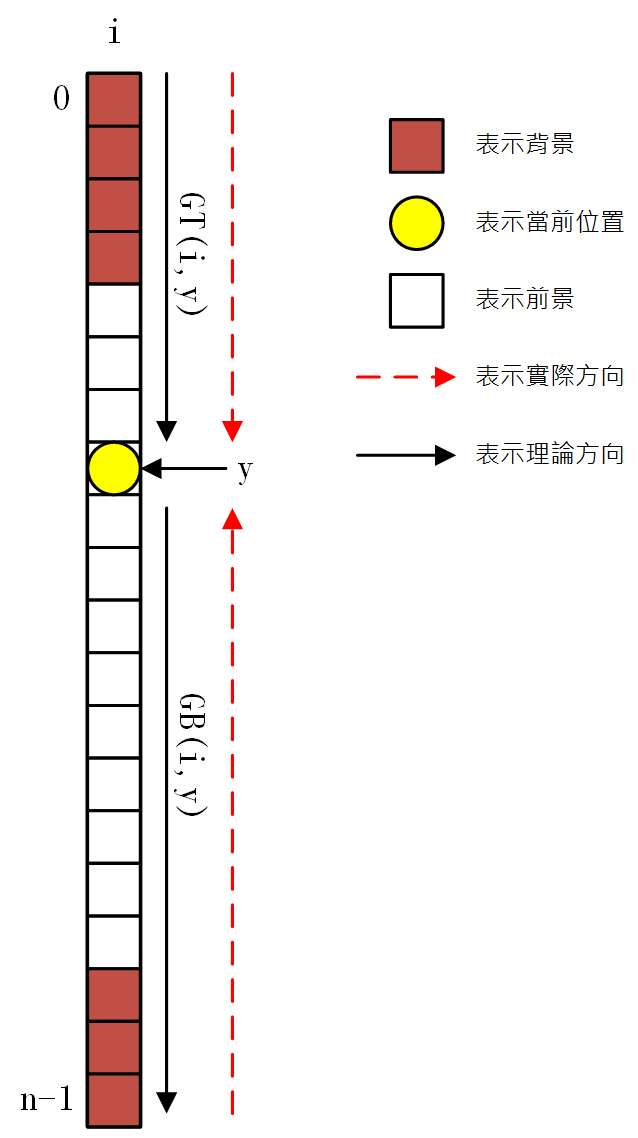
這樣，每列$G(i,y)$的計算就要分爲兩輪遍歷進行，第一輪從上到下($0 \leq y < n$)(*scan 1*)，計算每個點的$GT(i,y)$值；第二輪從下到上($n-2 \geq y \geq 0$)(*scan 2*)，計算每個點的$GB(i,y)$值，并於之前計算的$GT(i,y)$值比較取最小值記錄在緩存$g(i,y)$中。這樣第一階段的代碼框架已形成。如下圖。

另外説明，實際實現過程可將$\infty$取爲圖像的寬高和$(m+n)$。

The Second phase

第二躺遍歷全圖是按行遍歷，此時假設$y$為常數，將$G(i,y)$表示為$ g(i)$。這次遍歷就需要計算EDT、MDT或CDT。先將這三種距離計算方式統一成如下形式。 $$ DT(x,y) = \min{(i:0\leq i < m : f(x,i))} \tag{1} $$

其中，

$$ f(x,i) = \begin{cases} (x-i)^2 + g(i)^2, & \text{EDT} \\ |x-i| + g(i), & \text{MDT}\\ \max{(|x-i|, g(i))}, & \text{CDT} \end{cases} $$

另用$F_i = x \mapsto f(x,i)$表示儅取固定$i$值時關於$x$的函數。例如，對於EDT，$F_i$是一條頂點在$(i, g(i))$処的二次曲綫；對於MDT則是一條V-型折綫；對於CDT則是一條擁有最小值限定的V-型折綫。如下圖所示。

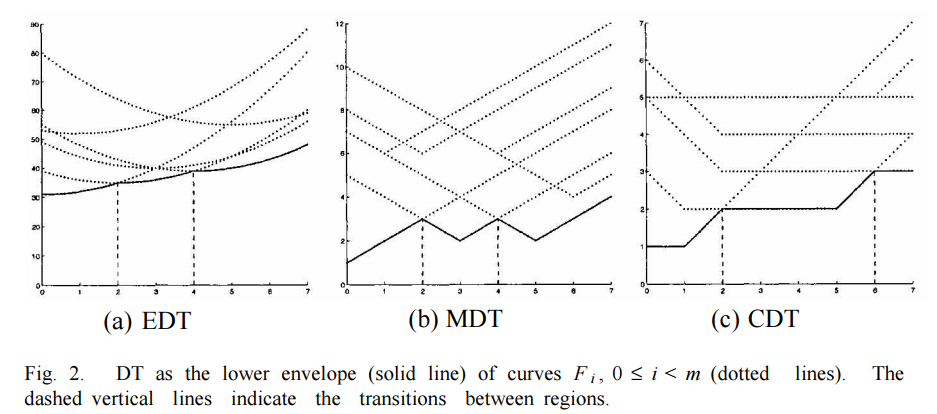
從上圖可以看出，我們要求得的結果就是一簇$F_i,(0\leq i < n)$組成的最低位包絡綫（圖中實綫部分）。這些包絡綫由許多小段曲綫構成，從左到右記爲$s[0], s[1], \cdots s[q]$。

繼續抽象函數$DT(x,y)$，將其中$i$的上限$m$替換爲一個變量$u$。 $$ FL(x,u) = \min{(i:0 \leq i < u:f(x,i))} $$

明顯，$DT(x,y) = FL(x,m)$。

再定義 $$ H(x,u) = \min{(h: 0\leq h < u \wedge \forall{(i:0\leq i < u:f(x,h))}: h)} $$

其含義是，固定列號為$x$時，從$0 \backsim u$列最小值位於第$h$列。這樣，$FL(x,u) = f(x, H(x,u))$，因此$DT(x,y) = f(x, H(x,m))$。這樣就把問題轉換為$H(x,m)$的計算。現在再定義兩個集合$S(u)$和$T(h,u)$。

$$ \begin{align} S(u) &= \{H(x,u)\mid 0\leq x < m\}\\ T(h,u) &=\{x \mid 0 \leq x < m \wedge H(x,u) = h\}\ \text{if}\ 0\leq h < u \end{align} $$

$S(u)$表示在每行中，最小值在$0\backsim u$範圍内哪個位置。而$T(h,u)$表示最小值位置在$h$処的$x$取值有哪些。顯然，$S(u)$是個非空集合，且可改寫爲$S(u) =\{ h \mid T(h,u) \neq \emptyset\}$。

説到這裏，已經輸入太多信息有點混亂了，整理下。前面提到當我們找到最低包絡綫時，就能確定最終結果了，那上面提到的這些函數或集合中，$S(u)$和$T(h,u)$就是我們要求得最低包絡綫的數學表示。其中$S(u)$表示哪個函數$F_i$在$T(h,u)$給出的$x$取值範圍下構成最低包絡綫。這樣第二階段的算法框架也差不多顯現出來。與第一階段類似，要進行兩趟遍歷，第一趟遍歷(*scan 3*)就是爲了確定最低包絡綫。第二趟遍歷(*scan 4*)就是計算最終結果了。下面是第二階段算法實現框架。

下面詳細説説最低包絡綫實際如何獲得。計算最低包絡綫本質是一個不斷迭代更新的過程。假設最低包絡綫由$q+1$個片段構成，$S(u) = {s[0], s[1], \cdots, s[q]}$，其中$s[l]$表示第$l$段是由哪個$F_i$函數確定。儅新的$F_u$輸入進來時，會有下面三種情況，可參考圖片。

a). $F_u$完全位於之前所構成的最低包絡綫之上，此時更新$S(u+1) = S(u)$，$T(u,u+1) = \emptyset$；

b). $F_u$完全位於之前所構成的最低包絡綫之下，此時更新$S(u+1) = {u}$，$T(u,u+1)= [0,m)$，因爲此時之前的最低包絡綫完全被$F_u$取代；

c). $F_u$與之前所構成的最低包絡綫相交，計算交點，添加新的最低包絡綫到$T(u,u+1)$。

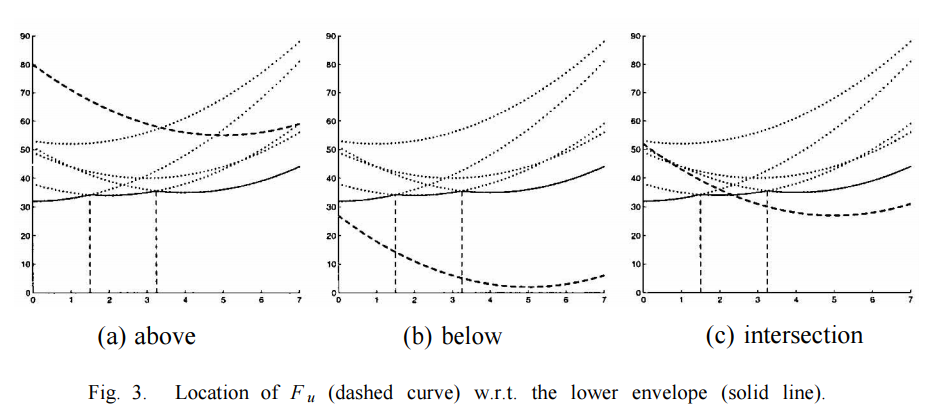
假設$t[l]$記錄了每段包絡綫的起始點位置，其中$l = q, q-1, \cdots$。從右至左遍歷最低包絡綫，直到找到滿足$F_u(t[l^{*}]) \geq F_{s[l^{*}]}(t[l^{*}])$的$l^{*}$，取$x^* = t[l^*]$或$x^*$為新交點的位置。如果$l^{*} = q$且$x^{*}\geq m$，則為情況a)；如果$l^* < 0$，則為情況b)；其他則爲c)。

下面説説情況c)中，$x^*$如何求。這裏引入$Sep(i,u)$函數用於$x^*$的計算，該函數計算得到第一個大於或等於$F_u$和$F_i$交點的整型值。 $$ F_i(x) \leq F_u(x) \Leftrightarrow x \leq Sep(i,u) \tag{2} $$

根據上面信息可知，$x^* = Sep(s[l^*], u)$，這樣最終的問題都集中在函數$Sep(i,u)$的計算，而該函數與我們選擇哪種距離度量方式相關。下節中將詳細説明函數如何設計。

在回過頭看代碼，其並不涉及浮點運算，而且利用兩個數組$s[\ ]$和$t[\ ]$就完成整個更新過程。其中數組$s[\ ]$就是用於記錄第$l$段最低包絡綫是由哪個$F_i$函數確定的；$t[\ ]$用於記錄每段最低包絡綫的位置；$q$用於記錄每次開始搜索的最低包絡綫序號。

（這裏有種情況一直沒想明白，假設已知$F_i$最低包絡綫，現添加$F_u$滿足其完全在$F_i$下方，這時代碼中更新$q = 0$，$s[0] = u$。假設添加$F_{u+1}$時，依然滿足條件$f(t[q], s[q]) > f(t[q], u+1)$，那此時依然更新$q = 0$, $s[0] = u+1$，但是我不理解的是，如果$F_u$和$F_{u+1}$實際是有交點的呢？）

Derivation of the Function Sep

下面説説$Sep$函數，它與你采用哪種距離度量函數相關。先來看最簡單的EDT度量函數。根據公式(2)可知：

$$ \begin{align} F_i(x) \leq F_u(x) &\Leftrightarrow (x-i)^2 + g(i)^2 \leq (x-u)^2 + g(u)^2 \\ &\Leftrightarrow x\leq (u^2 - i^2 + g(u)^2 - g(i)^2)\ \mathbb{div}\ (2(u-i)) \end{align} $$

其中，$div$表示整除。這樣EDT的$Sep$函數為： $$ Sep(i,u) = (u^2 - i^2 + g(u)^2 - g(i)^2)\ \mathbb{div}\ (2(u-i)) $$

接著看較複雜點的$Manhattan$度量函數。這裏需要分情況討論。如下圖。

根據前面分析和函數的性質的可知，$i < u$，并且每條曲綫$F_i$都是在$(i, g(i))$処取到最小值點。那麽基於這兩點結合函數圖像：

  • 儅$F_u$完全在$F_i$上方時，此時$g(u) \geq F_i(u)$，這就得到$g(u) \geq g(i) + u-i$；
  • 儅$F_u$完全在$F_i$下方時，此時$g(i) > F_u(i)$，這就得到$g(i) > g(u) + u-i$；
  • 其他情況，$F_i$與$F_u$相交，且相交位置發生在$F_i=x-i + g(i)$與$F_u = u-x + g(u)$的地方。

根據分析，我們可以定義，儅$F_u$完全在$F_i$上方時，$Sep$函數可以返回$+\infty$；儅$F_u$完全在$F_i$下方時，$Sep$函數可以返回$-\infty$；儅兩者相交，則： $$ Sep(i,u) = (g(u)-g(i) + u+i)\ \mathbb{div}\ 2 $$

綜上，$Manhattan$度量的$Sep$函數如下：

$$ Sep(i,u) = \begin{cases} \infty, & \text{if }g(u) \geq g(i) + u - i\\ -\infty, & \text{if }g(i) > g(u) + u - i\\ (g(u) - g(i) + u + i)\ \mathbb{div}\ 2,& otherwise. \end{cases} $$

最後討論最複雜的$Chessboard$度量函數，其也需要分情況討論。分爲兩個情況，每個情況又有三種子情況。可結合下圖分析討論。

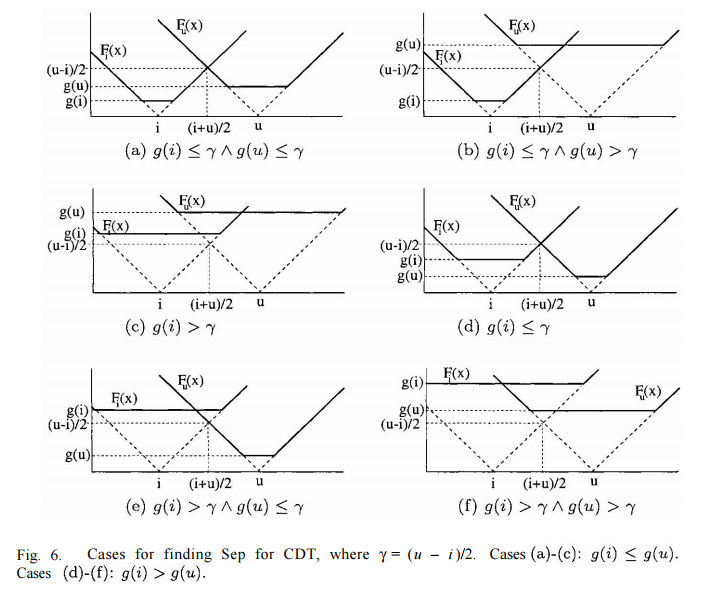
這裏先説明下$Chessboard$的度量函數$f(i,y) = \max{(|x-i|, g(i))}$，這個函數限制了最小值為$g(i)$，因此在圖像中會有一段平坦的區域，并且該平坦區域以$u$為中點對稱。

基於這些特點，我們將情況劃分為以下兩大類：

  1. $g(i) \leq g(u)$；
  2. $g(i) \geq g(u)$；

而每個大類中又分爲三個子情況：

a. $F_i(x)$的增區域與$F_u(x)$的減區域相交;

b. $F_i(x)$的增區間與$F_u(x)$的平坦區相交，且與$F_u(x)$減區域的延長綫有交點；

c. $F_i(x)$的增區間與$F_u(x)$的平坦區間相交，且$F_i(x)$增區間延長綫與$F_u(x)$減區間延長綫有交點。

這裏描述的情況可以對應上圖。

現假設$\gamma$表示$i$與$u$中點的函數值，例如上圖圖(a)中 $$ F_i(\gamma) = F_u(\gamma) = F_u \left(\frac{i+u}{2}\right) = \frac{u-i}{2} $$

結合圖(a)~圖(c)，交點位置左側均滿足$F_i(x) \leq F_u(x)$，圖(a)交點位置為$x^* = \frac{i+u}{2}$，圖(b)~圖(c)交點位置為$x^* = i + g(u)$。這樣結合起來，在$g(i) \leq g(u)$情況下，交點位置計算如下： $$ g(i) \leq g(u) \Rightarrow (F_i(x) \leq F_u(x)) \Leftrightarrow x \leq \max{(\frac{i+u}{2}, i+g(u))} $$

同理可得圖(d)~圖(f)中的交點位置為： $$ g(i) > g(u) \Rightarrow (F_i(x) > F_u(x)) \Leftrightarrow x \geq \min{(\frac{i+u}{2}, u-g(i))} $$

最終結合可得到$Chessboard$度量的$Sep$函數如下：

$$ Sep(i,u) = \begin{cases} \max{({(i+u)}\ \mathbb{div}\ {2}, i+g(u))},& \text{if }g(i) \leq g(u)\\ \min{({(i+u)}\ \mathbb{div}\ {2}, u-g(i))},& \text{otherwise} \end{cases} $$

這裏另外説明一個問題，爲什麽在CDT中，不會出現$F_i(x)$函數完全包含$F_u(x)$的情況，因爲如果出現這種情況，那麽不能滿足$i <u$這個大前提了，所以只可能出現上面討論的這些情況。

Parallelization, Timing Results, and Conclusions

文中作者也提到該算法可以并行計算，同樣給出了并行計算的時間對比表格，如下；

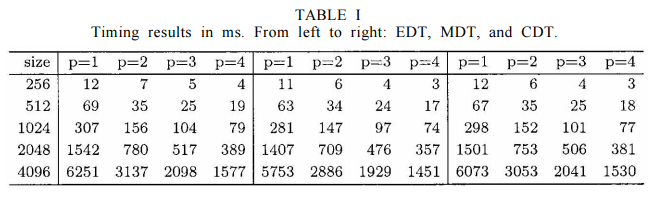
作者給出了該算法的時間複雜度為$\mathcal{O}(mn)$，如果并行其時間複雜度為$\mathcal{O}(mn/p)$，$p$為并行數。

當然該算法也能很容易推廣到$d$維空間的距離變換下。

至此，該論文閲讀完畢，實現細節請自行斟酌，并不複雜。