算法系列 Timsort排序算法原理學習
Contents
最近在實際應用中頻繁遇到快速排序算法(qsort)最壞情況,其實際耗時遠超過想象。主要原因在於進行排序的數據并非完全無序的,因此借此機會瞭解了當下使用廣汎的排序算法Timsort,特此記錄。本文不涉及具體代碼實現,但是會結合自己實現過程給出僞代碼,如有錯誤歡迎指正。
本文會從原理出發給出各個部分實現僞代碼,最後再討論細節。
Timsort原理介紹
本文對Timsort背景就不多做介紹,網上有很多資料,想瞭解也可以Wiki[4]下。但是,用Wiki上的一句話介紹Timsort,就是
|
|
|
|
整體框架
下面先説説現實數據有什麽特點:不會是完全隨機的,局部都會存在排好序的情況。Timsort作者稱這種局部自然形成的有序片段為natural runs。假設某一組數據都是由這些natural runs組成,那麽直覺上就能知道,使用歸并排序很快就能獲得最終結果。實際中,Timsort也是這麽做的。這樣,就能推出,我們要將輸入的數據切分成若干個natural runs,那麽如何切分?這是個人覺得Timsort算法第一個巧妙地地方。
算法中設置了最小片段長度MIN_RUN_LEN,從頭開始掃描數據,記錄當前有遞增序或遞減序的數據長度,算法會根據應用提供的比較函數選擇一種序,如果是逆序則會翻轉成正序,再進行後續操作。
如果滿足MIN_RUN_LEN,那麽將該片段壓棧;如果不滿足MIN_RUN_LEN,那麽用二分插入排序算法將長度凑到MIN_RUN_LEN。這裏爲什麽用二分插入排序,個人理解是,二分排序在數據量小的情況下效率高,而且不用消耗大量緩存空間,可以實現Inplace insert。到目前爲止,Timsort的整體框架已經可以搭建好,下面給出它的僞代碼。

二分插入排序
插入排序就是標準的方式進行,因爲是在已知序中插入新的元素,所以采用二分法插入,再加上MIN_RUN_LEN一般取值比較小,所以效率不會太差。下面給出這部分僞代碼。

歸并排序
Timsort中的合并runs本質上與歸并排序并沒有什麽區別,但是在性能上做了優化。在理想情況下,合并長度相近的run能提高效率。如果使用霍夫曼樹的歸并策略需要花費大量時間在選擇優先合并的run上,因此,Timsort選擇了一種折中的方案,它要求最右側的三個run長度滿足兩個條件[1]:
換而言之,從runs長度從左到右是遞增的,這樣我們從右到左合并時,就能保證runs的長度大致相同,達到平衡。下面給出不同情況下如何合并。

實現框架如下:

注意,在框架下多了條件判斷
這是因爲有大神測出Timsort算法原始實現存在bug,并提供了修改建議,详细可参考[2]。
下面説説歸并算法的實現:
已知兩個已排好序的序列$S_i$和$S_j$,長度分別為$l_i$和$l_j$。
Step1. 取出$S_j[0]$,從左到右在$S_i$中查找插入的位置,記爲$k_i$;
Step2. 取出$S_i[l_i-1]$,從右到左在$S_j$中查找插入的位置,記爲$k_j$。
Step3. 將剩餘的$S_i[k_i, l_i)$與$S_j[0,k_j]$進行歸并,其歸并要滿足將短的$run$向長的$run$插入的原則。
另外仔細琢磨下可以發現,在剩餘的兩段數據$S_i[k_i, l_i)$和$S_j[0,k_j]$中
這部分實現框架如下:

至此,其實Timsort已經可以完結。接下去的内容就是一些細節問題,例如,已經提供了MIN_RUN_LEN的設置,爲什麽還要根據輸入數據長度調整一次?什麽是Galloping Mode…有興趣的可以繼續往下看,也可直接翻看原作者的説明[3]。
算法細節
Galloping Mode
先來説説什麽是Galloping Mode,簡單說,就是作者對最終歸并過程的一個優化,先進行粗略搜索,在進行精確定位。
這裏不妨假設有兩個$runs$,$(run_1, run_2)$,長度分別爲$l_1$和$l_2$,且$l_1 < l_2$。根據上面的分析可知,$run_1$和$run_2$都是有序的,且$run_1[0] \geq run_2[0]$,$run_1[l_1-1] \geq run_2[0, l_2)$。
在Galloping Mode下,會將 $run_1[0]$ 與 $run_2[0],\ run_2[1],\ run_2[3],\ run_2[5],\ \cdots ,\ run_2[2^k -1],\ \cdots,$ 這些位置比較,直到滿足$run_2[2^{(k-1)} - 1] < run_1[0] \leq run_2[2^k-1]$停止,這是粗略搜索部分。經過這步就可以把搜索範圍縮小到$2^{(k-1)}-1$個連續的數據内,再直接使用二分搜索就能在最多$k-1$次對比操作下得到結果。
這裏會有一個疑問,爲什麽在粗略搜索部分不直接就使用二分搜索?作者也在文檔[3]給出了原因。
|
|
Galloping Mode這種方式加速也並不是沒有缺點的:
在比較時需要頻繁調用加速函數,這部分開銷可能無法接受;但是設計為inline函數,這部分結構又太冗長。
有時加速結構的比較次數要大於直接的綫性比較。可以參考作者給出的比較表格。
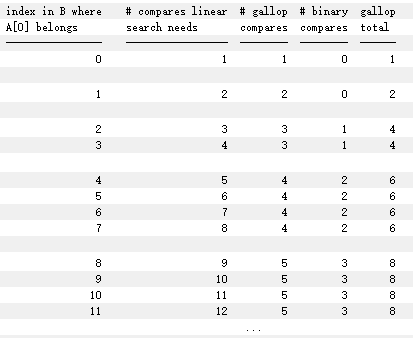
這樣,作者就設計了進入Galloping Mode的條件以及一些獎懲方式。下面簡單説明。
算法一開始先進行綫性的歸并,此時記錄下連續歸并次數,例如,連續$n$次都是$run_1$中的元素填入歸并區,若$n >= min\_gallop$時(初始$min\_gallop = MIN\_GALLOP$),我們就認爲之後的歸并操作可以啓用Galloping Mode。但是在綫性歸并過程中,如果發生變化都需要重置$n$值。作者將$MIN\_GALLOP$設爲$7$(應該是參考上面的表格得來的)。
只要在Galloping Mode中,連續歸并次數都大於$MIN\_GALLOP = 7$,就一直保持在Galloping Mode下。每進行一次加速,$min\_gallop$都要減少$1$,這樣保證下次更容易進入加速模式。但是,一旦退出Galloping Mode,就要將$min\_gallop += 2$作爲懲罰。這樣保證在數據是在兩個序列閒交替填入歸并區時,不會或較難進入加速模式,而導致效率降低。
下面給出這部分的僞代碼,這裏假設從$run_1$歸并到$run_2$中(從左到右歸并);從$run_2$歸并到$run_1$中類似。


調整Min_Run_Len
最開始時,提到過儅數據長度若小於MIN_RUN_LEN時,直接進行二分插入排序。那麽這個值取多少合適?另外在$\mathit{Algorithm 1}$中有$AdjustMinRunLen()$的函數,這是如何根據輸入數據長度調整MIN_RUN_LEN的?爲什麽要調整?這些在作者提供的文檔[3]中依舊能找到答案。這裏也簡要説明下。
首先,爲什麽要調整?之前提到的合并條件是爲了讓合并的兩個$runs$長度接近,這樣歸并效率才高。另外,因爲每次是兩個$runs$合并,所以,$runs$的個數最好是$2$的冪次方個。
現在假設數據長度 $ L = 2112, MIN\_RUN\_LEN = 32 $,那麽 $N_{runs} = \frac{L}{MIN\_RUN\_LEN} = 66 \backsim 0$,根據之前合并條件,能知道最後兩個$runs$的長度分別是$2048$和$64$,那麽這樣做合并顯然效率不高。如果我們將$MIN\_RUN\_LEN$調整爲$33$時, $N_{runs} = \frac{L}{MIN\_RUN\_LEN} = 64 \backsim 0$,這種情況顯然是我們希望看到的。所以,調整$MIN\_RUN\_LEN$是爲了讓$runs$數量等於或略小於2的冪次方,這樣有利於後面的合并。
現在我們知道爲什麽要調整MIN_RUN_LEN值了,那接下來就是如何調整了。依舊假設$MIN\_RUN\_LEN = 32 = 2^5$,數據長度為$L$
取$L$的低$5$位(若$MIN\_RUN\_LEN = 64$則取低6位,以此類推),這些bit中有被置位為$1$,則記$r = 1$,否則$r = 0$;
不斷將$L$向右移位,直到恰好小於$MIN\_RUN\_LEN$,記爲$n$,其取值範圍為$[MIN\_RUN\_LEN / 2 , MIN\_RUN\_LEN - 1]$
最後的取值為$n + r$
作者在文中建議,MIN_RUN_LEN的初始取值可以是$16,32,64,128$,其他不建議,如果選擇會損失其他部分的性能。建議取值$64$。
預分配Runs_Stack的空間
最後説下$Runs$的棧空間如何預分配,根據作者對與入棧runs的假設:
可以看出,在棧中的runs形成了一個遞減序列,只要不滿足前面設定的歸并條件,那麽run是要一直入棧的,那麽這個棧最大值就可以按如下方式計算。
假設棧長度為$s$,待排序元素長度為$n$,$MIN\_RUN\_LEN = m = 16$。runs的長度從左到右為遞減序列,那麽最右側的run的最小長度為$b[1] = 1$(爲什麽為$1$,因爲最後剩餘的元素個數最小值是$1$,這種情況也得入棧進行歸并),倒數第二個run最小長度為$b[2] = m$,這樣根據假設就能得到如下序列:
$$
1,\ m,\ m+2,\ 2 * m + 3,\ 3 * m + 6,\ \cdots,\
$$
序列可以表示爲:
這些runs的長度總和為$n$,且$n$最大整型值為$2^{64}-1 = 18446744073709551615$,這樣就得到:
$$
n = B[s] = b[0] + b[1] + b[2] + \cdots + b[s] \leq (2^{64}-1)
$$
可以發現,這個序列本質就是Fibonacci數列,這樣就能計算出棧的最大長度$s$了,計算結果可參考下表。另外説明,$s$的取值與$m$取值相關,但是由於Fibonacci數列在後期增長非常快,$m$的大小對$s$影響并不明顯,所以按照$m=16$得到的最大長度值足夠使用。
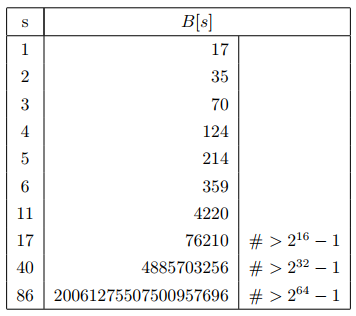
根據上表結果,Runs的棧大小取為$85$即可。
參考資料
[1] Timsort原理学习
[2] Proving that Android’s, Java’s and Python’s sorting algorithm is broken (and showing how to fix it)
[3] listsort
[4] Timsort - Wiki