本章又是數學的内容，主要介紹采樣相關的方法與數學工具——蒙特卡洛積分、Metropolis方法等。這些技術在全局光照和路徑追蹤等方面得到有效利用。本章二十幾頁的内容其實并沒有説清楚很多事，所以需要自行查找或補充一些知識才能搞懂。比如，Measure（測度）這個概念，在原書第二版中文版中，被翻譯成度量，通篇讀下來感覺非常怪異，最後查找資料發現應該稱它為測度，可以說測度論是現代概率論的基石[1]，兩者的關係可以類比成微積分和數學分析閒的關係，這裏就不多説了，有興趣可以自行查找資料。之後的内容我會盡量表達清楚，并把查閲的相關資料補充在後面，也限制於自己的能力，如有錯誤或不足歡迎指正。

14.1 Integration

本節將“積分”和“測度”這兩個概念結合説明，並以最常見的某個區域面積計算來復習相關積分以及測度的一些知識。

假設有二維實數平面$\mathbb{R}^{2}$，存在一個測度函數$\it{A}$，輸入$\mathbb{R}^{2}$内的某個子集，其能返回一個非負實數值，這個值就是通常意義下該平面子集的面積。這裏，測度函數$\it{A}$的定義域為$\mathbb{R}^{2}$的所有子集，我們記爲$\mathcal{P}(\mathbb{R}^{2})$，這樣我們可以用下面的形式描述函數$\it{A}$： $$ \it{A}:\mathcal{P}(\mathbb{R}^{2}) \rightarrow \mathbb{R}^{+} $$

通常也會用如下形式描述： $$ \mu: \mathcal{P}(\mathbb{S}) \rightarrow \mathbb{R}^{+}, \ \text{其中 }\mathbb{S} = \rm{(x,y)}, \rm{(x,y)} \in \mathbb{R}^{2} $$

該函數有如下幾個性質：

  1. $\mu(\emptyset) = 0$,
  2. $\mu(A \cup B) = \mu(A) + \mu(B) - \mu(A \cap B)$

將上面定義面積的測度函數改寫爲積分形式： $$ \mu(S) \equiv \int_{x \in S}\rm{d}\mu(\rm{x}) $$

其含義就是獲取區域S内的所有點x，并對它們的微分面積求和。下面這些寫法與其等效。 $$ \int_{S}\rm{d}A,\ \ \int_{\mathbf{X} \in S}\rm{d}\rm{x}, \ \ \int_{\mathbf{X}\in S}\rm{d}A_{\rm{x}},\ \ \int_{\mathbf{X}}\rm{d}\rm{x} $$

從這個簡單的例子可以發現，測度本質上就是一個函數，是將某個集合中的子集映射成一個數的函數。有了標準的面積測度函數，我們可以爲其添加一些特性，例如我不希望計算面積時，每個點的權重都是相同的，我希望它距離越遠權重越大。例如，在區域$[0,1]^2$内，標準面積按如下方式計算： $$ \int_{\rm{X} \in [0,1]^2}\rm{d}A(\rm{x}) $$

添加“放射性”權重后： $$ \int_{\rm{X} \in [0,1]^2}||\rm{x}||^2 \rm{d}A(\rm{x}) = \int_{x =0}^{1}\int_{y = 0}^{1}(x^2 + y^2) \rm{d}x\rm{d}y $$

如果我們將$||\rm{x}||^2$與$\rm{d}A$項結合考慮，那麽這就是新的測度函數，我們可以記爲$\nu$，這樣就可以用$\nu{(S)}$替換原來的積分。

14.1.1 Measures and Averages

測度函數的一個應用就是求在其下的均值。假設計算函數$f$在區域$S$上計算關於某種測度$\mu$的均值: $$ \rm{average}(f) \equiv \frac{\int_{x\in S}f(\rm{x})\rm{d}\mu(\rm{x})}{\int_{x\in S}\rm{d}\mu(\rm{x})} $$

舉例説明，函數$f(x,y) = x^2$在區域$[0,2]^2$上關於面積的均值： $$ \rm{average}(f) \equiv \frac{\int_{x=0}^2\int_{y=0}^{2}x^2\rm{d}x \rm{d}y}{\int_{x=0}^{2}\int_{y=0}^{2}\rm{d}x\rm{d}y} = \frac{4}{3} $$

換句話説，均值的多少，與你選取的測度函數相關，通常要選取一個相對於應用來講natrual的測度函數，例如上面說的對面積的測度函數。那什麽樣的測度函數算natrual的呢？下面用直綫的例子來説明。

14.1.2 Example: Measures on the Lines in the 2D Plane

通常在二維平面上，我們會用$y = mx + b$來參數化一條直綫，這樣直綫在”斜率-截距“空間中就表示為一個點$(m,b)$，如下圖。

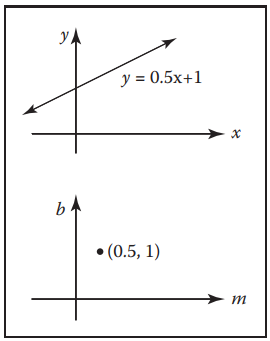
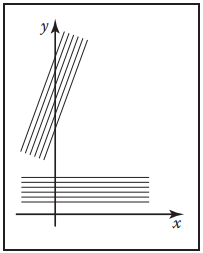
“斜截式”直綫最直觀的測度函數是關於${d}m\ {d}b$的，但是這個並不好。因爲它不具備“旋轉平移不變性”。換而言之，就是有一束平行綫，其水平穿過區域$[0,1]^2$和斜$45^{\circ}$穿過所得到的結果不同，因爲其測度函數中的截距$\rm{d}b$發生了變化。如下圖所示。左圖為上述描述的情況，右圖是將兩束直綫的截距調整為相同時，它們在平面中的表示，可以發現它們的斜率不同。這顯然也不是我們希望看到的。

\br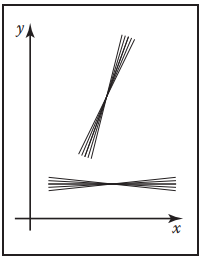

這個例子説明，我們希望一個natrual的測度函數具有旋轉平移不變性。

這樣我們考慮下圖，我們將$(m,b)$空間變換爲$(\phi, b)$空間，其中$\phi$表示直綫與水平方向的夾角，$b$表示直綫與y軸的截距。乍一看，感覺和$dm\ db$形式沒有區別，但是，只要加上一項就能使得它滿足我們的要求。

$$ d\mu = \cos{\phi}\ d\phi\ db $$

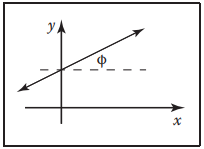
乘上$\cos{\phi}$后，相當於將截距投影到垂直直綫方向上，保證了截距的旋轉不變性。同樣，通過變換，也能很容易的將該式變換到其他坐標空間下表示。例如變換到$(m, b)$空間下： $$ d\mu = \frac{dm\ db}{(1+m^2)^{\frac{3}{2}}} $$

變換到直綫參數化為$ux+vy+1 = 0$的$(u,v)$空間下： $$ d\mu = \frac{du\ dv}{(u^2+v^2)^{\frac{3}{2}}} $$

或是"截距式“($a$表示x軸截距，$b$表示y軸截距)： $$ d\mu = \frac{ab\ da\ db}{(a^2 + b^2)^{\frac{3}{2}}} $$

還有一種直綫表示空間——霍夫空間（霍夫變換使用的直綫空間），如下圖。該空間下用直綫和原點的垂直距離和直綫法綫與x軸的夾角來定義，即$(\rho, \theta)$，因此一組直綫測度在該空間可表示為某個面積。這樣直綫可表示爲： $$ x\cos{\theta} + y\sin{\theta} - \rho = 0 $$

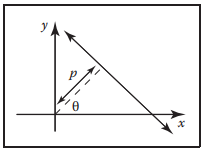
這樣，在該空間下的測度微分量可表示為： $$ d\mu = d\rho\ d\theta $$

以上這些測度表示都是等效的，具體使用依實際情況而定。

14.1.3 Example: Measure of Lines in 3D

下面説説三維空間中直綫的測度。我們知道，三維空間中的直綫通常需要四個維度來表示，例如，在$xy$平面上的某個點$(x,y)$和直綫在球坐標係下的方位角$(\theta, \phi)$，這樣一條直綫就表示為$(x,y,\theta, \phi)$。這樣，與二維空間類似，三維空間中直綫的測度微分量為: $$ d\mu = dx\ dy\ \sin{\theta}\ d\theta \ d\phi $$

其中$\sin{\theta}$是爲了保證直綫束在角度變化時有相同的測度。

我們還可以用球面上兩個點表示三維空間中的直綫$(\theta_1,\phi_1,\theta_2,\phi_2)$，其測度微分量為： $$ d\mu = \sin{\theta_1}\ d\theta_1\ d\phi_1\ \sin{\theta_2}\ d\theta_2\ d\phi_2 $$

另外還可以用兩個不重合的橫截面上的點表示，例如在$z = 0$上點$(x = u, y= v)$和$z=1$上點$(x = s, y= t)$表示直綫為$(u, v, s,t)$，但這種方式不適合直綫在接近平行$xy$平面時，而在接近平行$z$軸時也只能做到下面方式的近視： $$ d\mu \approx du\ dv\ a\ ds\ dt $$

14.2 Continuous Probability

本節主要也是復習概率論一些知識，熟悉的可以直接跳過。

14.2.1 1D Continuous Probability Density Functions

連續隨機變量(continuous random variable)$x$，它的分佈利用概率密度函數(probability density function, pdf)$p$描述，因此，$x$在某個區間$[a,b]$上的概率可以利用下面方式計算： $$ \mathrm{Probability}({x}\in[a,b]) = \int_{a}^{b}p(x)dx $$

pdf有下面兩個特性：

  • $p(x) \geq 0$

  • $\int_{-\infty}^{+\infty}p(x)dx = 1$

14.2.2 1D Expected Value

期望描述了某個一維函數$f$，在pdf為$p$下的平均值。用$E(f(x))$表示，記爲： $$ E(f(x)) = \int{f(x)p(x)dx} $$

期望有一個非常有個用的性質——加法性質，該性質在蒙特卡洛積分應用中非常重要。即： $$ E(f(x) + g(y)) = E(f(x)) + E(g(y)) $$

14.2.3 Multidimensional Random Variables

圖形學中，許多問題都是在高維空間中進行的，這樣我們就需要多維隨機變量來描述問題，幸運的是，多維隨機變量與一維情況沒有本質區別。依舊以面積測度爲例，假設空間$S$表示球體的表面，現有一測度$\mu$用於計算面積，我們可以定義一個概率密度函數$p$，使它滿足$p:S \rightarrow \mathbb{R}$，再定義一個隨機變量$x$，滿足$x \backsim p$，這樣我們就能計算$x$在區域$S_i \subset S$的概率： $$ \mathrm{Probability}(x\in S_i) = \int_{S_i}p(x)d\mu $$

結合之前説的測度，如果$S$表示某個面積，則$d\mu = dA = dx\ dy$；如果$S$是表示單位球上的一系列方向，則$d\mu = d\omega = \sin{\theta}\ d\theta\ d\phi$。

14.2.4 Variance

方差，概率論中總是和期望一起出現的量，在一維隨機變量中，其定義爲： $$ V(x) \equiv E([x - E(x)]^2) $$

工程中用的是其代數等價表示，其要求變量是獨立的： $$ V(x) = E(x^2) - [E(x)]^2 $$

另外，從方差可以知道標準差$\sigma$，其反映了與期望閒的絕對偏差： $$ \sigma = \sqrt{V} $$

14.2.5 Estimated Means

**獨立同分佈(independent identically distributed, iid)**隨機變量是指，隨機變量$x_i$閒相互獨立，但是它們都滿足相同概率密度函數$p$。現實中許多問題可以表示為一系列獨立隨機變量總和，我們在求期望時，直觀的會將這些變量求和后除以變量個數得到平均值，但是這樣只是近視結果： $$ E(x) \approx \frac{1}{N}\sum_{i=1}^{N}x_i $$

但是隨著$N$的增大，估計方差會隨之減小，只有黨$N\rightarrow \infty$時，才能得到真實值。利用大數定理可知： $$ \mathrm{Probability}\left[ E(x) = \lim_{N\rightarrow \infty}\frac{1}{N}\sum_{i=1}^{N}x_i \right] = 1 $$

這在之後使用蒙特卡洛積分進行Path Tracing時就能發現，采樣位置越少，出來的結果與真實情況差距越大，反之。

14.3 Monte Carlo Integration

本節就是本章的一個重頭戲——蒙特卡洛積分，但是也僅僅是粗略的説明，如果想知道爲什麽蒙特卡洛積分有效，可以參考博文[3]，裏面給出了數學證明。

現在先來定義下蒙特卡洛積分，假設函數$f\ :\ S \rightarrow \mathbb{R}$，隨機變量$x\backsim p$，那麽$f(x)$的期望可以用如下方式近似求得： $$ E(f(x)) = \int_{x\in S}f(x)p(x)d\mu \approx \frac{1}{N}\sum_{i=1}^{N}f(x_i) \tag{14.1} $$

這就是蒙特卡洛積分，它是個無偏估計，即儅$N \rightarrow \infty$時，等式(14.1)是可以取等號的。證明過程詳見博文[3]。等式(14.1)中的積分通常會習慣寫成$g = fp$的形式，這樣等式(14.1)可改寫為如下形式。 $$ \int_{x\in S}g(x)d\mu \approx \frac{1}{N}\sum_{i=1}^{N}\frac{g(x_i)}{p(x_i)} \tag{14.2} $$

其中，儅$g$取非零值時，$p$必須為正。換而言之，就是我們以概率密度為$p(x_i)$在函數$g(x)$上進行采樣，采樣結果的平均值用來近似積分$\int g(x) d\mu$的結果。這樣，概率密度函數$p(x_i)$的選擇就顯得非常重要，這就稱爲重要性采樣(importance sampling)。

在回顧等式(14.1)，其也反映出蒙特卡洛積分的一個問題：diminishing return。因爲方差的比例係數為$\frac{1}{N}$，標準差比例係數為$\frac{1}{\sqrt{N}}$。爲了讓估計誤差和實際誤差相似，那麽每降低一半誤差，需要將$N$增大原來的$4$倍。另一種減小誤差的方式就是采用分層采樣(stratified sampling)的方式，簡單説就是將采樣域$S$劃分成幾個子域$S_i$了，最終結果由這些子域$S_i$結果總和求得。圖形學中最常見的例子就是像素采樣的抖動。

14.3.1 Quasi-Monte Carlo Integration

擬懞特卡羅積分，根據Wiki介紹，其是將原始蒙特卡洛積分采樣過程中使用的僞隨機數改爲低差異列。使用低差異列的優勢在於收斂速度較快，但是也會引起意想不到的走樣。

14.4 Choosing Random Points

下面介紹本章節另一個重頭戲——如何生成隨機點。圖形學中經常會在某個區域内進行均匀采樣的操作，例如在$[0,1]^2$内均匀采樣$(u_1, v_1) \backsim (u_N, v_N)$共$N$個點。但是，如果區域并非矩形區域，而是圓形區域——用極坐標$(r_i, \phi_i)$表示，那麽直覺中可能會按如下方式進行均匀采樣：在$[0,1]^2$區間内分別采樣出$(u_i, v_i)$，再將$(u_i, v_i)$通過尺度變換到$(0, R) \times (0, 2\pi)$區間中，最後在通過三角函數換算到實際使用的$(x_i, y_i)$中。即：

$$ \phi_i = 2\pi u_i\\ r_i = v_i R\\ x_i = r_i \cos{(\phi_i)}\\ y_i = r_i \sin{(\phi_i)} $$

這麽做其實根本無法獲得均匀采樣的效果，下圖展示了這種方式的采樣結果。

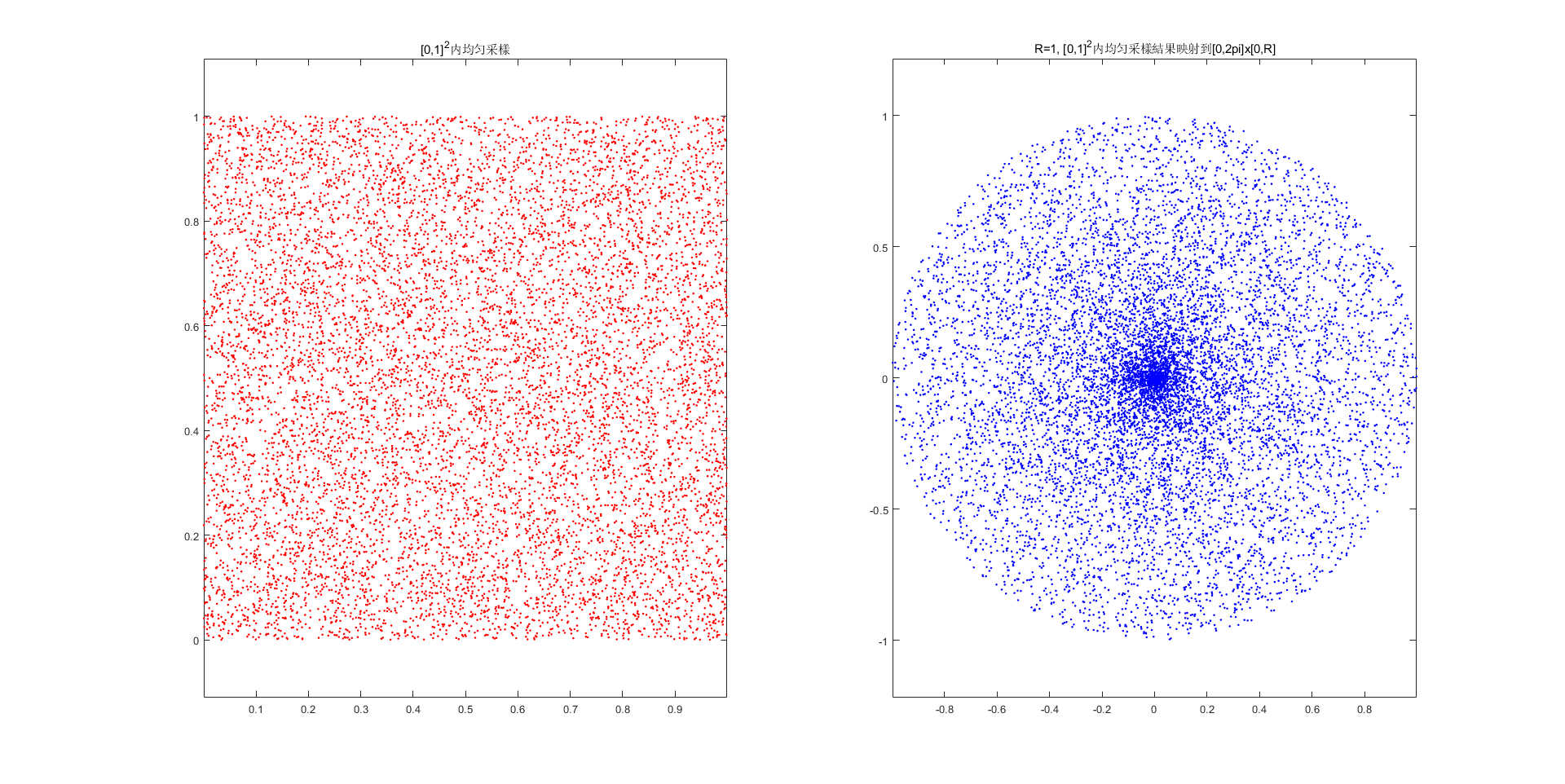
實際上，在$\phi_i$和$r_i$的確是在各自區間内均匀分佈，而造成這個結果原因是三角函數的非綫性變換造成的。

本節將介紹三種方法來獲取非矩形區域下均匀分佈的點，或是上面這種非均匀分佈的點。這三種方法是：反函數法(function inversion)、拒絕法(rejection)和Metropolis法。

14.4.1 Function Inversion

定義概率密度函數為$f(x)$，其定義域為$x\in[x_{min}, x_{max}]$，這樣可以從一組已知均匀分佈隨機數$\xi_i$$(\xi_i \in [0,1])$中生成具有概率密度為$f(x)$的隨機數$\alpha_i$。同時，定義纍積概率分佈函數(cumulative probability distribution function, CDF)$P(x)$： $$ \mathrm{Probability}(\alpha < x) = F(x) = \int_{x_{min}}^x f(x’)d\mu $$

爲了獲得想要的隨機數結果$\alpha_i$，對上式求其反函數，再將已知均匀分佈序列$\xi_i$帶入就可求得滿足概率密度為$f(x)$的$\alpha_i$： $$ \alpha_i = F^{-1}(\xi_i) $$

爲什麽能這麽操作是可行的？首先，我們已知CDF函數的值域是在$[0, 1]$内；其次，CDF函數在其定義域内是單調非減的；最後， 利用反函數其實就是將值域中均匀分佈的序列$\xi_i$映射囘定義域中，自然能獲得在概率密度為$f(x)$下均勻分佈的點。具體數學證明如下（參考[5])

已知

$$ \begin{cases} x_1 \leq x_2 \Rightarrow F(x_1) \leq F(x_2)\\[2ex] y_1 \leq y_2 \Rightarrow F^{-1}(y_1) \leq F^{-1}(y_2) \end{cases}\tag{14.3} $$

由反函數定義可知： $$ F^{-1}(y) < x,\ \text{iff }\ y < F(x) \tag{14.4} $$

由於均匀分佈的CDF函數如下：

$$ P(a \leq x) = H(x) = \begin{cases} 0, & x < 0\\ x, & 0 \leq x \leq 1\\ 1, & x \geq 1 \end{cases}\tag{14.5} $$

結合等式(14.4)和等式(14.5)可得： $$ P(F^{-1}(y) \leq x) = P(y \leq F(x)) = H(F(x)) $$

若只考慮$F(x)$的值域$[0,1]$，那麽可得： $$ P(F^{-1}(y) \leq x) = H(F(x)) = F(x) \tag{14.6} $$

由此可知，通過反函數可以獲得某個概率密度分佈下的均匀采樣點。但是，實際情況下，有些纍計概率分佈函數的反函數的解析解並不好求得，我們也可以采用數值方式獲得。

上面所説的都是一維情況，下面擴展到多維情況（以二維爲例）繼續説明。

假設一個隨機變量$\alpha = (\alpha_x, \alpha_y)$，其概率密度定義在$[x_{min}, x_{max}] \times [y_{min}, y_{max}]$中，那麽其分佈函數為：

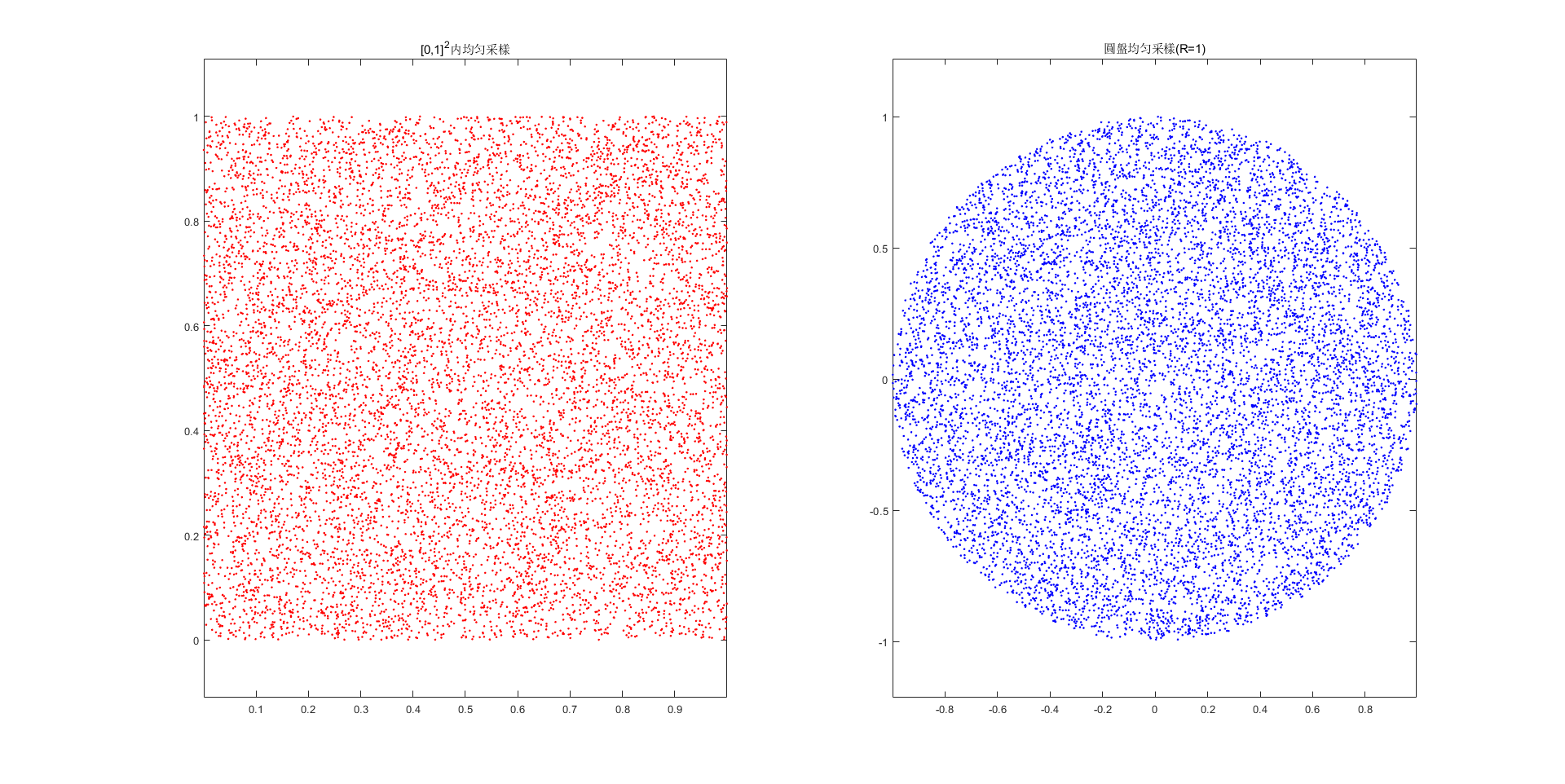
$$ \mathrm{Probability}(\alpha_x < x \text{ and } \alpha_y < y) = F(x,y) = \int_{y_{min}}^y\int_{x_{min}}^x f(x', y') d\mu(x', y') $$

以之前的圓盤爲例，若要進行均匀采樣，那麽其概率密度為 $$ p(x,y) = \frac{1}{\pi R^2} \Rightarrow p(r, \phi) = \frac{r}{\pi R^2} $$

那麽其二維分佈函數用極坐標表示如下：

$$ \mathrm{Probability}(r < r_0 \text{ and }\phi < \phi_0) = F(r_0, \phi_0) = \int_0^{\phi_0}\int_0^{r_0}\frac{r\ drd\phi}{\pi R^2} = \frac{\phi r^2}{2\pi R^2} \tag{14.7} $$

最終，利用等式(14.7)可分別求得邊緣密度函數$f(r)$和$f(\phi)$，接著獲得邊緣分佈函數$F(r)$和$F(\phi)$，最終利用反函數求得從已知均匀分佈的點對$(\xi_1,\xi_2)$變換到$(r, \phi)$的關係，具體求法參考[4]。

$$ \phi = 2\pi\xi_1 \\[2ex] r = R\sqrt{\xi_2} $$

采樣結果如下圖所示。

再整理下球體上的均匀采樣。在實時渲染中，反射光綫的方向我們都是用單位半球坐標表示的，即兩個方位角$\theta$和$\phi$。假設，我們所獲得的反射光綫服從下面的概率密度函數： $$ p(\theta, \phi) = \frac{n+1}{2\pi}\cos^n(\theta) $$

其中，$\theta$表示反射光綫與表面法綫的夾角，$\theta \in [0, \frac{\pi}{2}]$；$\phi$是方位角，$\phi \in [0, 2\pi]$；$n$為Phong-like指數。如下圖所示。

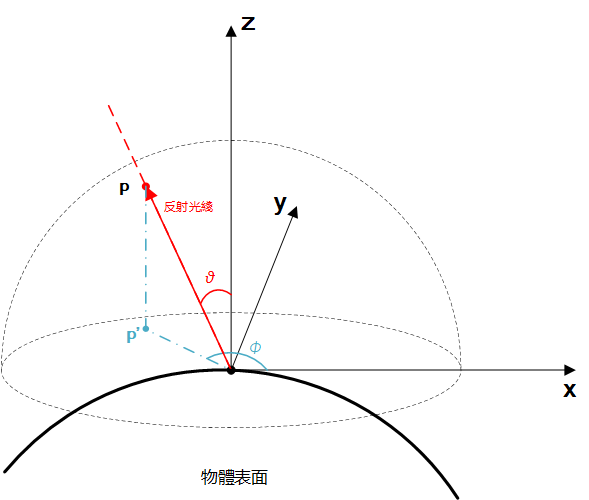
其概率函數為： $$ P(\theta, \phi) = \int_0^{\phi}\int_0^{\theta}p(\theta’, \phi’)\sin{(\theta’)}d\theta’\ d\phi’ $$

其中，$d\omega = \sin{\theta}d\theta\ d\phi$為球坐標係下微分項，因爲只關心方向，所以令$\rho = 1$。此時獲得邊緣分佈函數為：

$$ \begin{align} P_{\phi}(\theta) &= \int_0^{2\pi}\int_0^{\theta}p(\theta',\phi’)\sin{(\theta')}d\theta'\ d\phi' \\[2ex] &=\int_0^{2\pi}d\phi'\int_0^{\theta}p(\theta',\phi’)\sin{(\theta')}d\theta'\\[2ex] &=1 - \cos^{(n+1)}{(\theta)} \end{align} $$
$$ \begin{align} P_{\theta}(\phi) &= \int_0^{\frac{\pi}{2}}\int_0^{\phi}p(\theta',\phi’)\sin{(\theta')}d\theta'\ d\phi' \\[2ex] &= \int_0^{\frac{\pi}{2}}p(\theta',\phi’)\sin{(\theta')}d\theta'\int_0^{\phi}d\phi'\\[2ex] &= \frac{\phi}{2\pi} \end{align} $$

利用邊緣分佈函數的反函數可以從已知均匀分佈的點序列$(\xi_1, \xi_2)$，獲得在半球上均匀分佈的序列。

$$ \begin{array}{l} \theta = \arccos{((1-\xi_1)^{\frac{1}{n+1}})}\\[2ex] \phi = 2\pi\xi_2 \end{array}\tag{14.8} $$

假設，Phong-like指數$n=1$，已知球坐標係下方向向量$\vec{a}$可表示爲： $$ \mathbf{a} = (\cos{(\phi)}\sin{(\theta)}, \sin{(\phi)}\sin{(\theta)}, \cos{(\theta)})\tag{14.9} $$

將等式(14.8)結果帶入(14.9)可得： $$ \mathbf{a} = (\cos{(2\pi\xi_1)}\sqrt{\xi_2}, \sin{(2\pi\xi_1)}\sqrt{\xi_2}, \sqrt{1-\xi_2})\tag{14.10} $$

14.4.2 Rejection

Rejection方法本質非常簡單：從服從簡單分佈的點中，利用排除法選出符合某種複雜分佈的點。依舊以之前圓盤上均匀采樣爲例：我們先在$(x,y) \in [-1,1]^2$上均匀采樣出若干點$(x_i, y_i)$，又因爲已知點落在圓盤内的條件是$x^2 + y^2 \leq r^2$，所以，利用該條件將生成的點$(x_i,y_i)$中滿足條件的保留下來。如下圖所示，最右側為Rejection方式選出的結果。

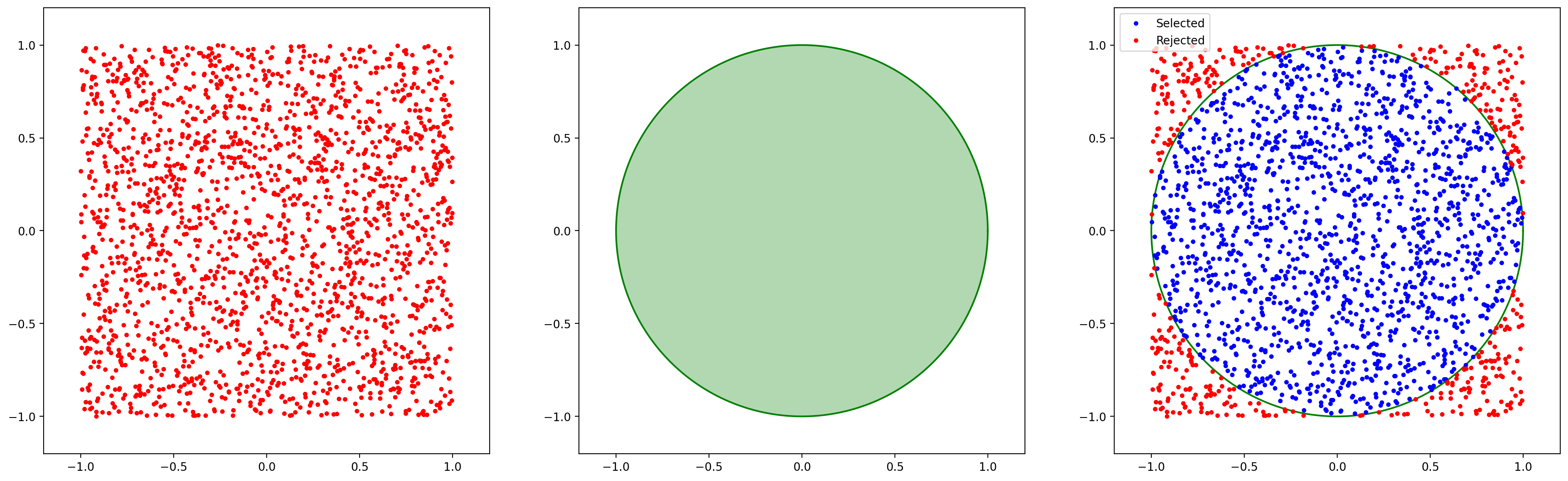
這一過程也可用下面僞代碼表示：

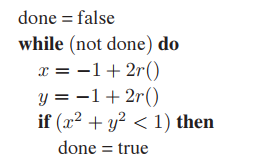
其中$r()$表示標準隨機數生成函數。

假如我們需要獲得服從某種特殊分佈的隨機點，利用Rejection方法同樣能夠實現。假設，已知需要獲得隨機數$x \backsim p$，$p : [a,b] \mapsto \mathbb{R}$，且對於所有$x$滿足$p(x) < m$。我們只需在$[a,b] \times [0, m]$的區間内均匀采樣，然後利用$y < p(x)$的條件挑選出結果，這樣就能獲得滿足分佈$p$的均匀采樣結果。如下圖。

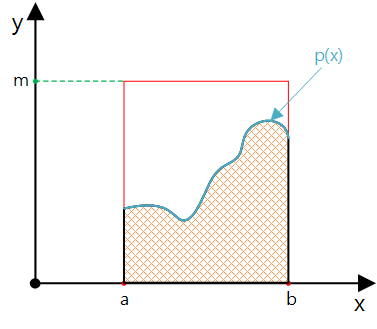
僞代碼如下：

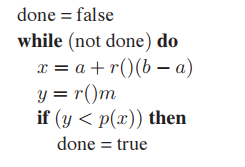
同理可以實現球面上的均匀采樣，實現方式如下：

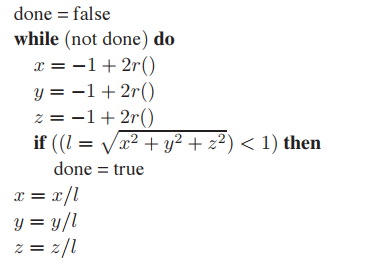
Rejection方法看起來比反函數法更簡單，實現起來也更容易，但是它還是有自己的缺點的，該方法無法和分層采樣結合使用，這導致其收斂速度變得更慢，因此這種方式主要用於調試或者特別困難的情況中。

14.4.3 Metropolis

首先，Metropolis是個人名，并不翻譯成大都市。再者，本節内容完全沒看懂，書上每個單詞都認得，連起來就是不明白講什麽。所以這裏也不按書上的内容整理了，而是根據查閲的資料和個人理解總結下Metropolis采樣方法吧！

14.4.3.1 馬爾科夫鏈

其定義非常簡單，某時刻$t$的狀態只依賴於其前一時刻$t-1$，用數學方式可描述為，假設狀態序列$\cdots, X^t, X^{t-1},X^{t-2},\cdots$，狀態$t$時刻的條件概率只依賴於$t-1$時刻，即 ： $$ P(X^t | X^{t-1},X^{t-2},\cdots,X^0) = P(X^t|X^{t-1})\tag{14.11} $$

儅存在多個狀態時，(14.11)可以表示為矩陣形式，稱爲狀態轉移矩陣，其中$P(i,j)$值為$P(j|i)$，表示從狀態$i$轉換到狀態$j$的概率。即： $$ X_t = X_{t-1}P_{t-1} $$

14.4.3.2 馬爾科夫鏈性質

以下描述前提都是，轉移矩陣$P$是唯一確定的，即每個時刻狀態閒的轉移概率不變。

  1. 若某個馬爾科夫鏈的某個狀態經過有限次轉移後回到自身，那麽稱這個馬爾科夫鏈具有周期性；
  2. 若某個馬爾可夫鏈中的兩個狀態之間可以相互轉移，稱這個馬爾科夫鏈可約；
  3. 如果某個馬爾科夫鏈既沒有周期性，也不可約，那麽稱這個馬爾科夫鏈是各態遍歷的。
  4. 各態遍歷的馬爾科夫鏈，無論初始狀態$(x_0^0, x_1^0, x_2^0, \cdots, x_k^0)$取值如何，經過有限次狀態轉移後，其狀態會趨於一個平穩分佈$X_s = (x_0^s, x_1^s, x_2^s, \cdots, x_k^s)$，即： $$ X^s = \lim_{t\rightarrow \infty}X^0 \ast P^t $$

這個性質可以理解爲：馬爾科夫鏈最終收斂結果只與狀態轉移矩陣有關，而與初始狀態無關[7]。

  1. 某個各態遍歷的馬爾科夫鏈，若平穩分佈$X^s$滿足： $$ x_i^s\ast P(i,j) = x_j^s \ast P(j,i),\ \ \text{for all }i,j $$

則稱$X_s$是該馬爾科夫鏈的平穩分佈，上式稱爲細緻平穩條件。進一步瞭解細緻平穩條件可參考博文[8]。

14.4.3.3 馬爾科夫鏈采樣

基於上面介紹的馬爾科夫鏈性質，結合前面的蒙特卡洛積分，可以對某個平穩分佈進行采樣。

假設已知平穩分佈狀態轉移矩陣$P$，及初始概率分佈$X^0$。經過$i$輪轉移後狀態為$X^i$，儅$n$輪后收斂到平穩狀態$X^s$，即： $$ X^n = X^{n+1} = X^{n+2} = \cdots = X^s $$

對於每個狀態有： $$ X^i = X^{i-1}P = X^{i-2}P^2 = \cdots = X^0P^i \tag{14.12} $$

具體過程如下：

其中$( X^{n_1}, X^{n_1+1}, \cdots, X^{n_1 + n_2 -1})$為需要的平穩分佈樣本集，將其帶入蒙特卡洛積分即可獲得結果。

這種采樣方式并未解決對任意分佈進行采樣，換而言之，對於任意一個平穩分佈，我們要如何獲得它的狀態轉移矩陣$P$？這就有了下面的MCMC采樣方式。

14.4.3.4 MCMC采樣 (Markov chain Monte Carlo)

前面提到了細緻平穩條件，只要矩陣$P$滿足該條件，就能將矩陣$P$作爲某個平穩分佈的狀態轉移矩陣。但是僅從細緻平穩條件依然很難找到合適的矩陣$P$。下面看看MCMC方法是如何處理的。

假設目標平穩分佈為$X^s$，隨機獲得一個狀態轉移矩陣$Q$，其很難滿足細緻平穩條件: $$ x_iQ(i,j) \neq x_jQ(j,i) $$

這裏引入一個新矩陣$\alpha$，通過它來讓等式成立： $$ x_iQ(i,j)\alpha(i,j) = x_jQ(j,i)\alpha(j,i) $$

那如何設計矩陣$\alpha$呢？只要滿足下面兩個式子即可： $$ \alpha(i,j) = x_jQ(j,i)\
\alpha(j,i) = x_iQ(i,j) $$

帶入細緻平穩條件很容易看出等號是成立的： $$ x_iQ(i,j)\alpha(i,j) = x_iQ(i,j)x_jQ(j,i) = x_jQ(j,i)x_iQ(i,j) = x_jQ(j,i)\alpha(j,i)\tag{14.13} $$

這樣新的狀態轉移矩陣為： $$ P(i,j)= Q(i,j) \alpha(i,j) $$

另外， $\alpha(i,j)$又稱爲接受率，表示新的狀態轉移矩陣$P$可以通過任意一個馬爾可夫鏈的狀態轉移矩陣$Q$以一定的接受率獲得。這麽說其實個人無法與代碼描述關聯起來，但是換個表述方式就很容易理解了：儅從狀態$i$以$Q(i,j)$的概率跳轉到狀態$j$時，我們以$\alpha(i,j)$的概率接受這個狀態轉移[9]，即大於等於$\alpha(i,j)$時接受狀態轉移，否則不接受。

具体算法流程如下：

其中$( X^{n_1}, X^{n_1+1}, \cdots, X^{n_1 + n_2 -1})$可以看做從目標平穩分佈中采樣得到的樣本集。

MCMC采樣在實際應用中依舊無法使用，原因在于接受率$\alpha(X_{i-1}, y)$可能非常小，導致采樣值大多數都被拒絕轉移，所以采樣效率很低，即$n_1$需要非常大。這個問題將在下一節的Metropolis-Hastings采樣算法中解決。

14.4.3.5 Metropolis-Hastings采樣

Metropolis-Hastings采樣是爲了解決MCMC采樣中接受率太小的情況，重新觀察等式(14.13)，不妨假設$\alpha(i,j) = a_1,\ \alpha(j,i) = a_2$，且$0< a_1 < a_2 < 1$，我們在等式(14.13)兩邊同乘一個放大因子$k$，使$k\cdot a_2 = 1$，即：

$$ \begin{align} x_iQ(i,j)a_1\cdot k &= x_jQ(j,i)a_2 \cdot k \\[2ex] \Rightarrow x_iQ(i,j)\cdot a_1k &= x_jQ(j,i)\cdot 1\\[2ex] \Rightarrow a_1^{\prime} = a_1k &= \frac{x_jQ(j,i)}{x_iQ(i,j)} \end{align} $$

又因爲接受率的取值範圍為$[0,1]$，所以上式可變爲： $$ \alpha^{\prime}(i,j) = a_1^{\prime} = \min{\left(1, \frac{x_jQ(j,i)}{x_iQ(i,j)}\right)} $$

通過上面變換可以看出，我們在提高接受率的同時，不僅沒有破壞細緻平穩條件，而且還能通過除法將狀態轉移矩陣約去，因爲轉移矩陣$Q$是任意選擇的，那麽就可以令$Q(i,j) = Q(j,i)$，這樣 $$ \alpha^{\prime}(i,j) = \min{\left(1, \frac{x_j}{x_i}\right)} $$

因此，M-H采樣算法如下

同樣$( X^{n_1}, X^{n_1+1}, \cdots, X^{n_1 + n_2 -1})$可以看做從目標平穩分佈中采樣得到的樣本集。

采樣的内容其實非常多，這裏只能結合書中結構，淺薄的整理些個人理解的東西（再一次體會到知道的越多越無知），有興趣的可以自行查詢資料。

Frequently Asked Questions

參考資料

[1] 概率论和实变函数（测度论）有什么联系？

[2] 为什么样本方差（sample variance）的分母是 n-1？

[3] 蒙特卡洛积分与重要性采样详解

[4] 均匀采样问题总结

[5] 逆采样(Inverse Sampling)和拒绝采样(Reject Sampling)原理详解

[6] Metropolis 采样算法

[7] MCMC(二)马尔科夫链

[8] 如何理解MCMC中的细致平稳条件？ - 石溪的回答 - 知乎

[9] MCMC原理解析(马尔科夫链蒙特卡洛方法)