圖形學系列 Games101-Homework3-NormalMaps and BumpMaps and DisplacementMaps

最近重新做了games101課程作業3，發現裏面bump_fragment_shader其實並不理解其原理，特別是TBN矩陣的使用，因此查詢資料補充，特此記錄。

Texture Mapping的缺點

先回顧Blinn-Phong光照模型：

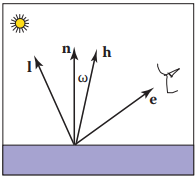
某個著色點的取值可以寫爲： $$ L = k_a I_a + k_d(\frac{I}{r^2})max(0, \mathbf{n}\cdot \mathbf{l}) + k_s(\frac{I}{r^2})max(0, \mathbf{n}\cdot \mathbf{h})^p $$

我們利用Texture mapping時，將其中的$k_d$替換為紋理圖中查詢的結果，這樣就能完成整個紋理映射工作。

在渲染過程中，我們會用大量的三角形來表示被渲染的物體模型，而每個三角形理論上都是“平坦”的，所以在每個三角形内部點的屬性都可以通過對三個頂點插值的方式獲得，這樣獲得的屬性值具有一定的變化連續性，但有時候反而會讓最終的結果失真，例如下面這張圖。

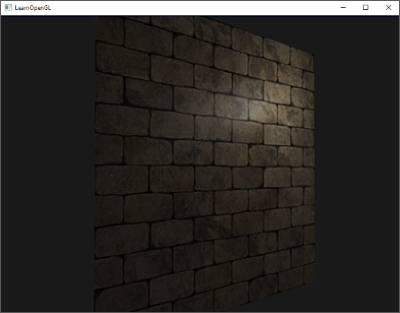
圖中的墻壁咋一看效果還不錯，但是仔細看可以發現，雖然每個磚塊縫隙清晰可見，但缺少了“凹凸感”，也就是缺乏細節，這樣讓整面墻看起來非常“平整”。而導致這一效果的原因在於平面法向量。因爲我們在對墻壁建模時，其就是一個平面，法向量均是朝向同一個方向，例如下面左圖

我們知道，一張圖内的物體要有“立體感”是需要光影的變化體現的。顯然相同方向的法向量不能產生這樣的效果，所以我們需要在建模時改變不同位置的法向量，例如上面的右圖，這就相當於在原本光滑的表面有了凹凸形變，這就能獲得我們想要的結果。下面就是采用這種方式獲得的圖像，對比兩者可以發現，添加法向量變化的結果明顯比原來的結果真實。

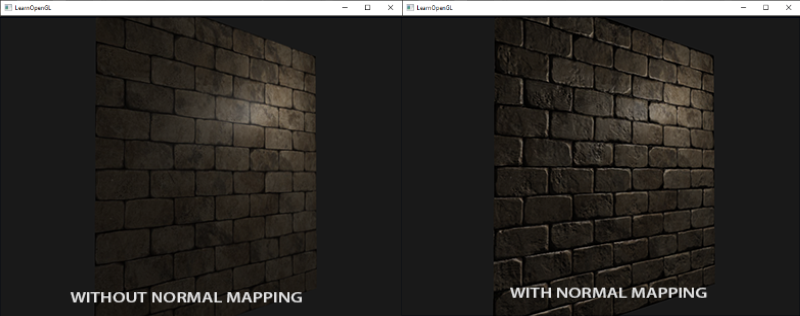
這樣的技術被稱爲Normal mapping或Bump mapping。

Normal Mapping

下面説説Normal Mapping是如何實現的，其實方式非常簡單。

我們通常采用RGB圖像來存儲紋理，相似的，可以采用RGB圖像來存儲法向量信息：利用R、G、B三值分別表示法向量的X、Y、Z三個軸。由於法向量通常是單位向量，每個方向取值範圍為[-1, 1]，而RGB取值範圍為[0, 1]，因此在存儲時需要做映射：

1

vec3 rgb_normal = normal * 0.5 + 0.5;	// transforms from [-1, 1] to [0, 1]

基於這個方式可得到上面墻面例子中的法向量圖。

可以看到這張法向量貼圖呈現出偏藍色，因爲法向量基本是在z-軸附近變化，所以導致整張圖片呈現藍色。而上圖中，在頂部磚塊邊緣呈現出綠色，説明該位置的法向量方向是更偏向y軸的。有了法向量貼圖和紋理圖，利用Blinn-Phong著色模型和fragment著色器就能得到理想的結果了。

雖然normal mapping效果不錯，但是其也是有限制的。首先，法向量貼圖中所表示的方向與平面法向量屬於同一個座標系下，例如世界座標系中；另一個就是法向量貼圖中所表示的方向大部分要與實際平面法向量朝向相似，也就是說假設平面法向量是沿著z-軸($(0,0,1)$)，法向量貼圖需要呈現出偏藍色；如果現在使用相同的法向量貼圖，而平面法向量朝向變爲沿著y-軸($(0,1,0)$)，這時得到的光照結果就不正確了，例如下圖所示。

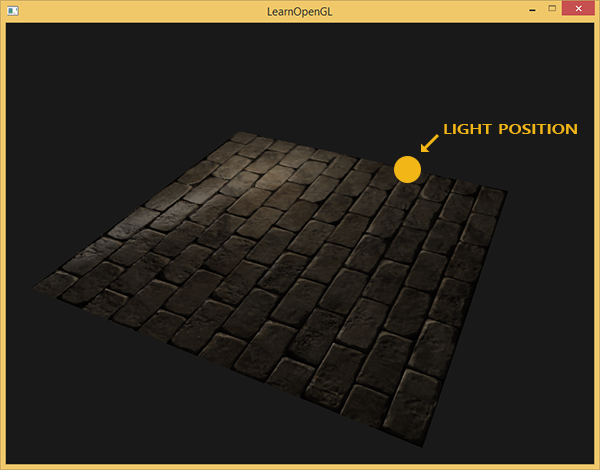
爲解決這個問題，一個辦法是為每個表面做單獨的法向量貼圖，這個辦法看似簡單，但實際中並不好操作，由於兩者要同屬一個座標系中，所以假設有一個立方體，則需要製作6個法向量貼圖，如果模型中有無數的朝向不同的表面，可想這個製作難度以及存儲難度有多大，而且當模型發生運動，還需要記錄模型的運動變換，這就導致這個方式使用非常不便。例如下圖所示， 圖中紅色箭頭表示法向量貼圖中獲得的法綫方向，黑色箭頭表示平面法向量，它們均在$xyz$的世界坐標系中定義。

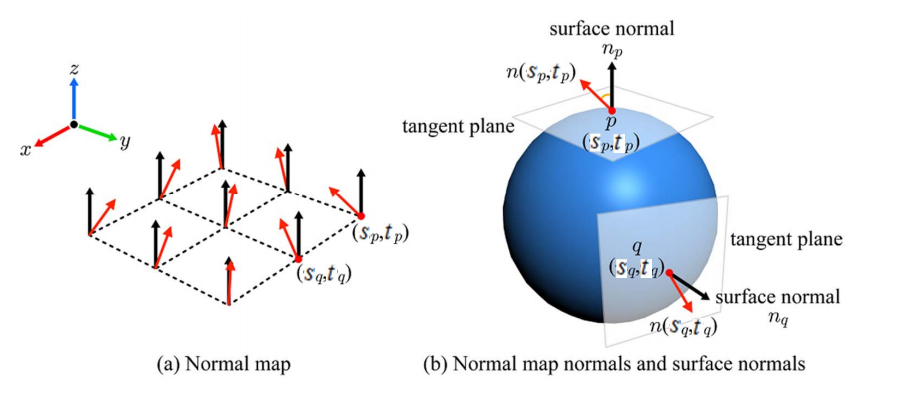
另一個解決辦法就是利用局部空間和坐標空間變換實現：定義局部空間為模型中每個位置的切平面與該位置上平面法向量構成，稱其為切向量空間(tangent space)。

Tangent Space

首先我們解釋下如何存儲的問題。定義切向量空間后，將每個位置實際用於渲染的法向量相對於其對應切向空間中的向量值存儲到法向量貼圖中，例如下圖所示，我們存儲圖中$n(S_p, t_p)$在$p$點処切向量空間中的取值。

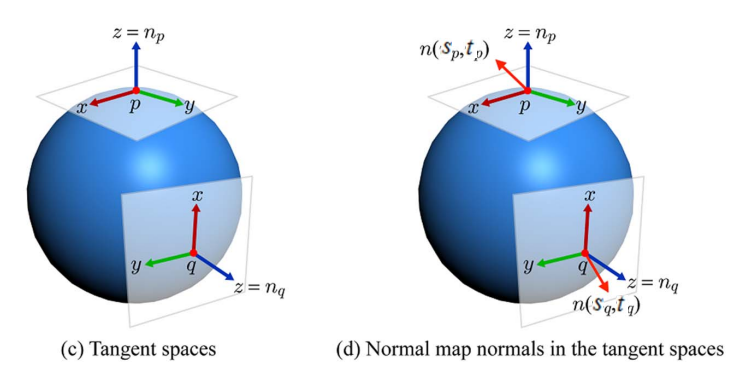
下面説説如何使用，顯然我們做渲染時，所有的向量都需要位於同一個坐標系空間中，例如世界坐標系，而現在我們將法向量存放在切向量空間中，那麽這之間需要進行坐標系的轉換。轉換的方式有兩種：

1. 一種是將切向量空間中向量轉換到世界坐標係中；
2. 一種是將世界坐標系下的向量轉換到切向量空間中；

這兩種方式孰優孰劣之後在討論，現在先引入TBN矩陣，該矩陣目的就是用於坐標系閒轉換。TBN矩陣中，$\mathbf{T}$代表Tangent vector，$\mathbf{B}$代表Bitangent vector，$\mathbf{N}$代表Normal vector。如下圖。

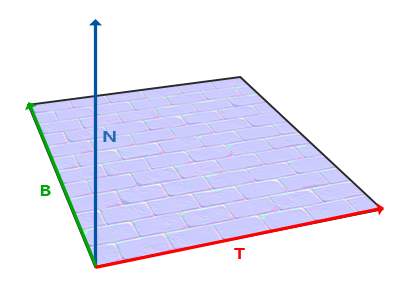
其中$\mathbf{N}$就是平面法向量方向，因此是可以從模型中獲得，現在就要計算得到$\mathbf{T}$和$\mathbf{B}$向量。再看上圖，我們構建TBN向量時，有意讓$\mathbf{T}$和$\mathbf{B}$兩個向量沿著紋理圖的xy-軸（或uv-軸）。這樣我們就能利用紋理坐標來計算$\mathbf{T}$和$\mathbf{B}$向量，看下圖。

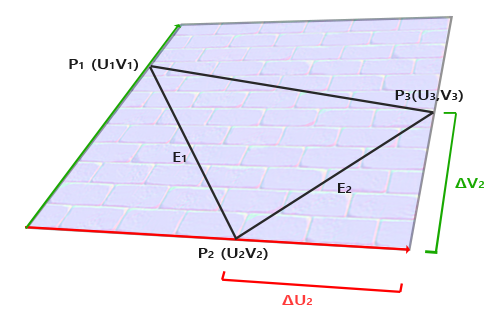
模型中某個三角形的三個頂點映射到紋理圖中$P_1$、$P_2$、$P_3$三個點，那麽如圖可得到下面關係。

由於$\mathbf{T}$和$\mathbf{B}$為基向量，我們將其展開可得：

改寫爲矩陣形式為：

這樣，通過矩陣運算就可獲得$\mathbf{T}$和$\mathbf{B}$這兩個基向量。

這樣我們就獲得了最終的TBN矩陣：

注意，向量$\mathbf{T}$、$\mathbf{B}$和$\mathbf{N}$均要轉換成單位向量。

現在這個TBN矩陣如果左乘一個向量，則意味著將該向量從切向量空間中轉換到世界坐標係空間中。那麽從世界坐標系中轉換到切向量空間，則使用TBN矩陣的逆矩陣完成，由於TBN矩陣是正交矩陣，所以其逆矩陣與其轉置矩陣相等，所以TBN矩陣對於空間之間的轉換是非常簡潔友好的。

進一步討論TBN矩陣

前面在舉例TBN矩陣時，我們假設了UV空間，即紋理空間是與平面法向量正交的，但是實際情況中不一定滿足這個條件，因此我們需要對其進行施密特正交化處理后才能使用：

再者，前面提到過坐標系轉換有兩種：從切向量空間轉換到世界坐標系空間；或從世界坐標系空間轉換到切向量空間。下面就討論下這兩種轉換的優劣。

從直覺出發，將法向量從切向量空間轉換到世界坐標系空間只需要轉換一個向量，非常簡單！從代碼角度看，對於每個三角形，TBN矩陣在fragment shader外計算好后傳入像素著色器，而在fragment shader内部需要對每個像素的法向量進行變換。例如下面代碼：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

typedef struct {
	vec3 FragPos;
	vec2 TexCoords;
	mat3 TBN;
	vec3 lightPos;
	vec3 viewPos;
}frag_shader_t;

{
	...
	fs_in.TBN = mat3(T, B, N);
	...
}

int fragment_shader(frag_shader_t fs_in){
	normal = texture(normalMap, fs_in.TexCoords).rgb;
	normal = normalize(normal * 2.0 - 1.0);   
	normal = normalize(fs_in.TBN * normal);
	...
}

接著我們看看第二種方式。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

{
	...
	fs_in.TBN = transpose(mat3(T, B, N));
	...
}

int fragment_shader(frag_shader_t fs_in){
	normal = texture(normalMap, fs_in.TexCoords).rgb;
	normal = normalize(normal * 2.0 - 1.0);   
	
	vec3 lightDir = fs_in.TBN * normalize(fs_in.lightPos - fs_in.FragPos);
	vec3 viewDir  = fs_in.TBN * normalize(fs_in.viewPos - fs_in.FragPos);  
	...
}

第二種方法在fragment shader中看似做的更多，但是，第二種方法中將世界坐標系轉換到切空間坐標系的操作并不是一定要在fragment shader中進行，可以將其移到vertex shader中處理。因爲，多數情況下，lightPos和viewPos不是每個fragment處理時都需要更新的，而對於FragPos，同樣也可以在vertex shader中計算出其切空間位置。這樣，在fragment shader中就不需要做空間轉換的工作，而第一種方法沒法做到這一點。基於這點，方法二中就不能將TBN矩陣送入fragment shader中，而是要將切空間中的光源位置、觀測位置和頂點位置送入著色器中。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

typedef struct{
	vec3 FragPos;
	vec2 TexCoords;
	vec3 TangentLightPos;
	vec3 TangentViewPos;
	vec3 TangentFragPos;
}frag_shader_t;

void main(){
	vec3 lightPos;
	vec3 viewPos;
	mat3 TBN = transpose(mat3(T, B, N));
	frag_shader_t frag_shader;
	
	frag_shader.TangentLightPos = TBN * lightPos;
	frag_shader.TangentViewPos = TBN * viewPos;
	frag_shader.TangentFragPos = TBN * vec3(model * vec4(position, 0.0));
	...
}

作業中的TBN

以上瞭解完TBN矩陣，滿懷期待的回頭閲讀作業三中的代碼，又傻眼了，作業中的TBN矩陣和之前介紹的完全不一樣。下面貼出來作業中TBN計算的提示。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

{
	...
	float kh = 0.2, kn = 0.1;

	// TODO: Implement bump mapping here
	// Let n = normal = (x, y, z)
	// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
	// Vector b = n cross product t
	// Matrix TBN = [t b n]
	// dU = kh * kn * (h(u+1/w,v)-h(u,v))
	// dV = kh * kn * (h(u,v+1/h)-h(u,v))
	// Vector ln = (-dU, -dV, 1)
	// Normal n = normalize(TBN * ln)
	...
}

仔細想想，我們構建TBN矩陣的目的是爲了統一計算時的坐標系，而以平面法向量為z軸，在切平面上構建局部坐標系是有無窮多組基的，所以之前介紹的TBN矩陣構建方式只是其中一種。現在再來看作業中的TBN矩陣構建方式。

由於平面法向量是已知的，那麽最關鍵的一步是構建出T向量：我們將平面法向量$ \vec{\mathbf{N}} $在$xyz$坐標系中拆分成$ \vec{\mathbf{N}}_{xz} $和$\vec{\mathbf{N}}_{y}$兩個向量，可見下圖，這三個向量均在同一平面$\mathcal{S}$内，那麽只需要將該平面繞其軸（該平面的法向量）旋轉$90^{\circ}$即可，換個思路就是將$\vec{\mathbf{N}}_{xz}$向量旋轉到$\vec{\mathbf{N}}_{y}$向量処。

具體操作如下，假設$\vec{\mathbf{N}}_{xz}$與$\mathbf{X}$軸夾角為$\theta$，那麽先將$\vec{\mathbf{N}}_{xz}$繞$\mathbf{Y}$軸旋轉$\theta$，再繞$\mathbf{Z}$軸旋轉$\frac{\pi}{2}$，最後繞$\mathbf{Y}$軸旋轉$-\theta$即可。將一系列旋轉操作作用于向量$\vec{\mathbf{N}}$即可得到向量$\vec{\mathbf{T}}$，再利用向量叉乘得到向量$\vec{\mathbf{B}}$，最後需要將$\vec{\mathbf{T}}$和$\vec{\mathbf{B}}$歸一化成單位向量即可。下面給出數學表示： $$ \vec{\mathbf{T}} = rotate_y(-\theta) * rotate_z(90^{\circ}) * rotate_y(\theta) $$

其中，

由圖像上可知，

帶入上面計算可得最終結果為：

以上就是作業中得到TBN矩陣的方式（另一方面可以看到作業中給出的提示是有錯誤的），其實像最開始説的那樣，形成TBN坐標系的基向量是無窮多的，只要在生成法向量貼圖和使用過程中使用方法統一，無論哪組基向量都行。至此作業中的TBN矩陣怎麽來的就搞明白了。

Bump Mapping

接著作業提示看，構造完TBN矩陣后不是直接與法向量相乘就是結果了嗎？後面$\mathrm{d}U$和$\mathrm{d}V$都是在算什麽？帶著這個問題，我繼續看了另一種貼圖方式——凹凸貼圖bump mapping。

所謂凹凸，就是物體表面有上下起伏所形成的溝壑或凸包；但凹凸貼圖本質也并未改變物體表面形狀，而是通過模擬凹凸表面的法向量來獲得視覺上的凹凸感。下面簡單介紹下原理^[5]，再看代碼就很清楚了。

假設某曲面上有一點$\mathbf{P}(u, v)$，其法向量可以由以下形式得到： $$ \mathbf{N} = \mathbf{P}_u \times \mathbf{N}_v $$

其中，

現在，我們在其法向量方向對$\mathbf{P}$點施加一個擾動，我們成該擾動函數為凹凸函數 $b(u,v)$。

這裏$\mathbf{n} = \mathbf{N} / |\mathbf{N}|$。

那麽添加擾動后，其法向量也發生相應改變，即： $$ \mathbf{N}^{’} = \mathbf{P}^{’}_u \times \mathbf{P}^{’}_v $$

其中,

假設，$b(u,v)$值非常小，那麽上式中最後一項可以被忽略。 $$ \mathbf{P}^{’}_u \approx \mathbf{P}_u + b_u \mathbf{n} $$

同理可得： $$ \mathbf{P}^{’}_v \approx \mathbf{P}_v + b_v \mathbf{n} $$

這樣我們就可以知道經過擾動后的法向量為：

凹凸貼圖中存儲的其實是某個位置中，沿著法向量高度變化的量，原本是一張灰度圖，由於其存儲占用大、信息少，所以凹凸貼圖的方式逐漸被normal mapping取代。如下圖所示，左邊為凹凸貼圖，右邊為法向量貼圖。

現在回到作業中，由於貼圖中的坐標系都是局部坐標系，法向量為其Z-軸， UV為其另兩個軸，高度變化是沿著法向量方向，所以，最終結果是$ (-dU, -dV, 1) $的形式，其中：

而利用圖像計算U，V方向的微分的方法也很簡單，即：

高度變化量為紋理圖中RGB像素的模長。這樣就能得到作業中想要的結果。

Displacement Mapping

無論是法向量貼圖還是凹凸貼圖，它本質只是修改了法向量的朝向，而并未改變物體表面的幾何形狀，這種方式又被稱爲假位移，那麽真位移自然就是改變了物體表面幾何形狀咯。參考下圖：

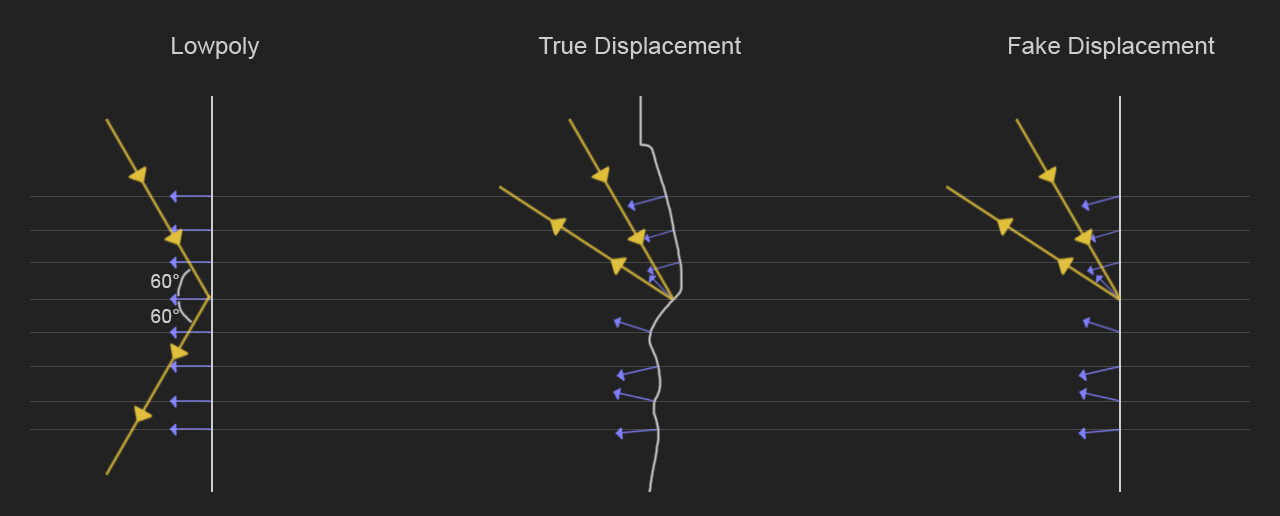
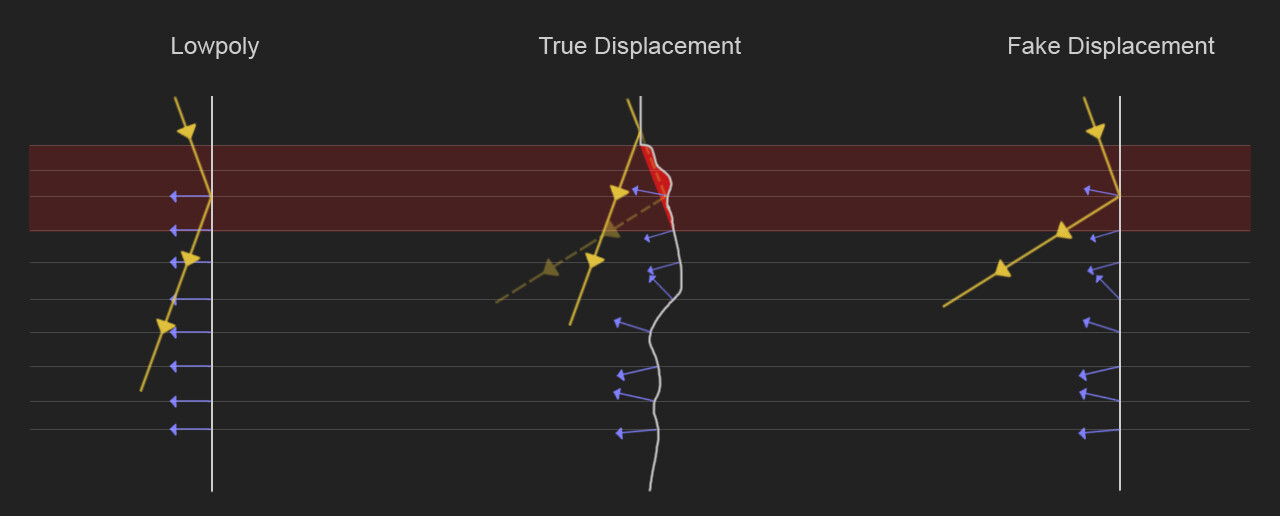
假位移貼圖雖然效果不錯，但是還是有一定的失真，比如自陰影的缺失，例如下圖，上圖為displacement mapping結果，下圖為normal mapping結果。

而陰影的缺失并不是光相互作用的唯一可見區別，通過不規則的真實位移，增加了物體表面，這導致更多的反射光，而使用假位移時，會導致暗部區域看起來形成不自然的黑色^[6]。對比下面兩張圖可以看出兩者閒的區別。

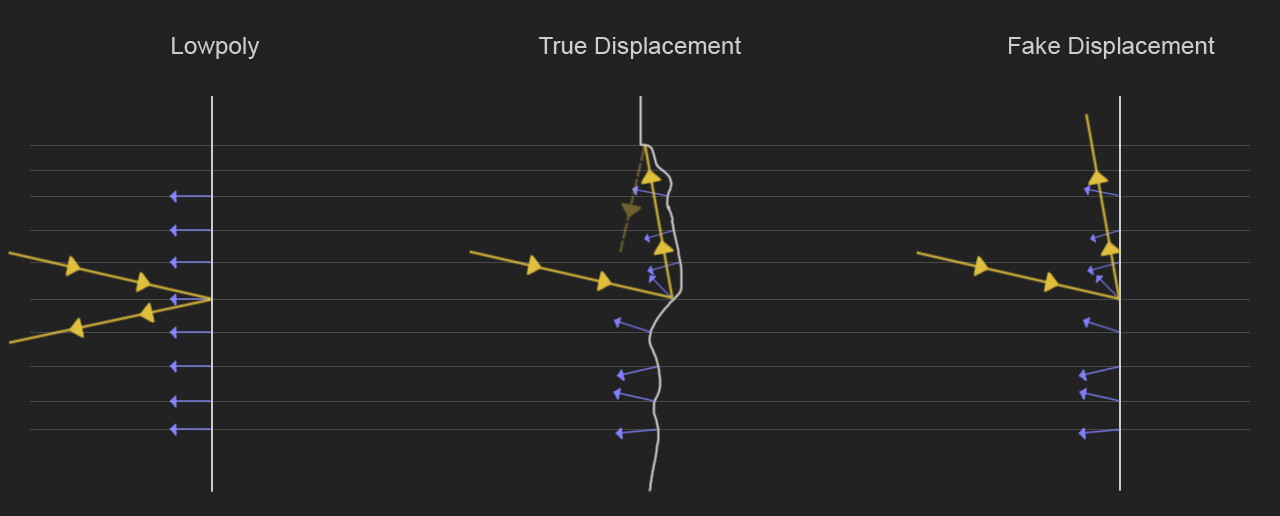
那麽對於作業中的displacement mapping的實現也很簡單，基於bump mapping結果，我們得到了TBN矩陣和高度偏移量以及法向量偏移方向。那麽我們只要將著色點移動到新位置即可。

參考資料

[1] Normal Mapping

[2] Normal vs Displacement vs Bump Maps: Differences and when to use which

[3] Chapter XI Normal Mapping

[4] 作业3 bump mapping中TBN的t 公式怎么推导的

[5] Hearn D, Baker M P, Baker M P. Computer graphics with OpenGL[M]. Upper Saddle River, NJ:: Pearson Prentice Hall, 2004.

[6] Fake vs True Displacement - Part 1/2