點是否在多邊形内
Contents
這是最近做項目過程中延申思考的一個問題——在平面上如何快速判斷點與任意多邊形的關係?上網查找一些相關資料,其中《Graphic GEM IV》中的論文《Point in Polygon Strategies》做了許多介紹與總結,特此記錄。
基本概念
Winding Number
以下介紹來自維基百科:
Suppose we are given a closed, oriented curve in the xy plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns that the object makes around the origin.
假设在xy平面上有一条有向的闭曲线。可以把曲线想象为某个物体的运动轨迹,运动方向就是曲线的方向。曲线的卷绕数就是物体逆时针绕过原点的总次数。
下面兩圖很形象的描述了Winding Number,圖片同樣來自維基百科。計算繞過原點的總次數時,逆時針方向的運動算正數,順時針方向的運動算負數。
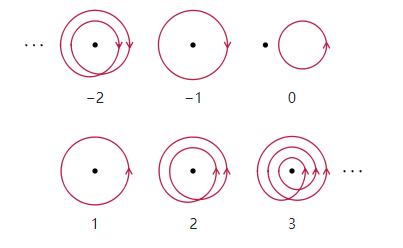

Jordan Curve
以下介紹來自維基百科
In topology, the Jordan curve theorem asserts that every Jordan curve (a plane simple closed curve) divides the plane into an “interior” region bounded by the curve and an “exterior” region containing all of the nearby and far away exterior points.
在拓扑学中,若尔当曲线(英语:Jordan curve)是平面上的非自交环路(又称为简单闭曲线,英语:simple closed curve)。若尔当曲线定理(英语:Jordan curve theorem)说明每一条若尔当曲线都把平面分成一个“内部”区域和一个“外部”区域,且任何从一个区域到另一个区域的道路都必然在某处与环路相交。
下圖同樣來自維基百科,黑色曲綫即爲Jordan Curve,它將平面區域劃分爲外部區域(紅色部分)和内部區域(藍色部分)。
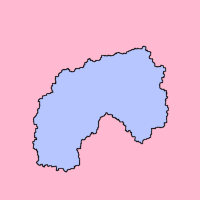
General Algorithms
Crossings Test
相交測試,這個方法原理非常簡單,但是細節上需要小心處理,特別是使用整型表示點時候。
相交測試,從測試點沿坐標軸(通常采用X軸正向)引出一條射綫,判斷該射綫與多邊形的邊的交點數的奇偶性,就能得到測試點是否落在多邊形内。
如下圖所示,一般性的情況下,交點數為奇數時,測試點在多邊形内;交點數為偶數時,測試點在多邊形外。
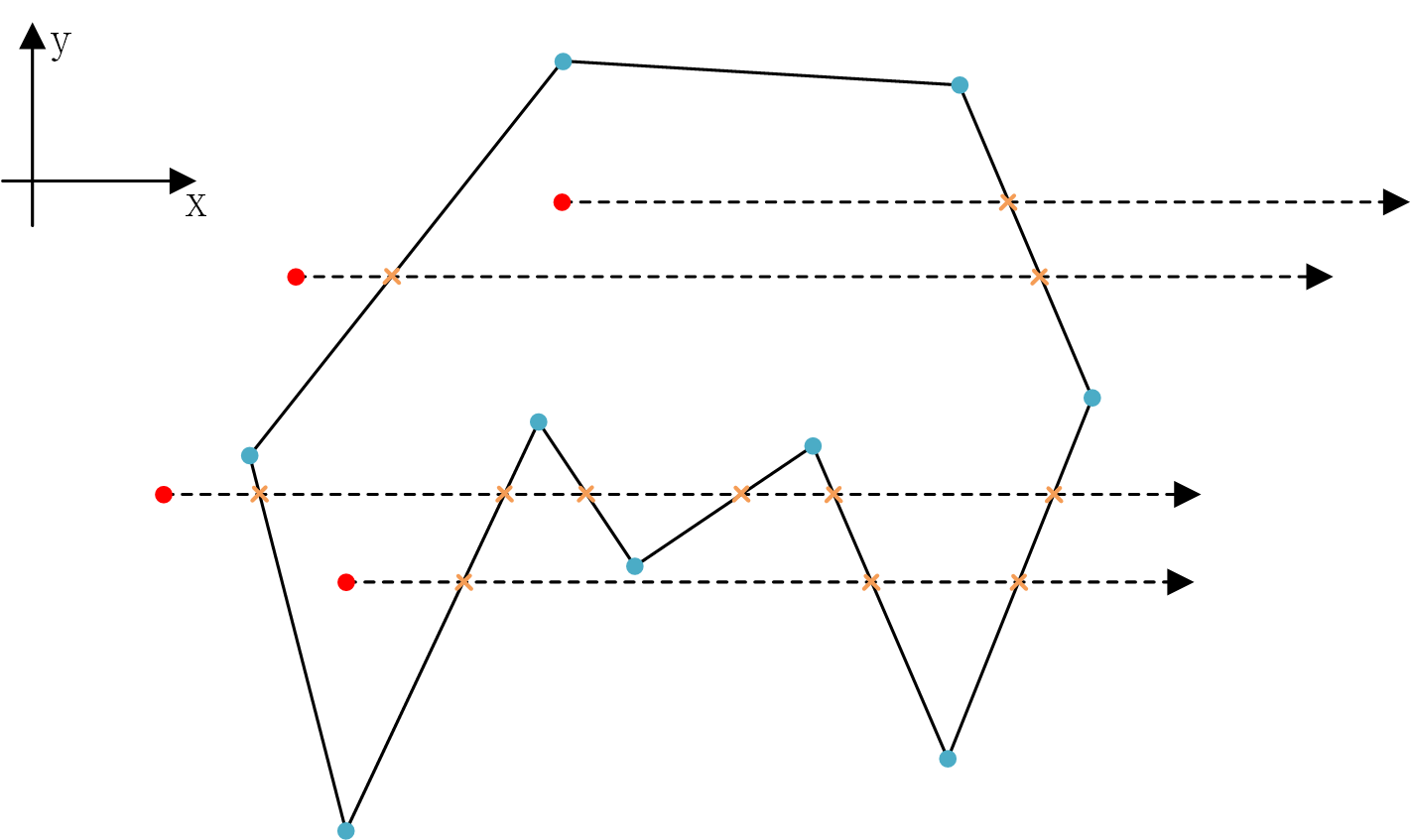
論文中給出了加速的做法,我們其實並不需要準確的計算出交點,所以只要判斷測試射綫和多邊形邊界有交點就行。那麽有以下情況:
- 儅多邊形邊界綫段兩個端點X軸坐標同時位於測試點右側(即沿X軸正向),兩個端點Y坐標異號,則增加交點數,否則不增加交點數;
- 儅多邊形邊界綫段兩個端點X軸坐標位於測試點兩側,計算交點坐標,若交點位於測試點右側,則增加交點,否則不增加交點數;
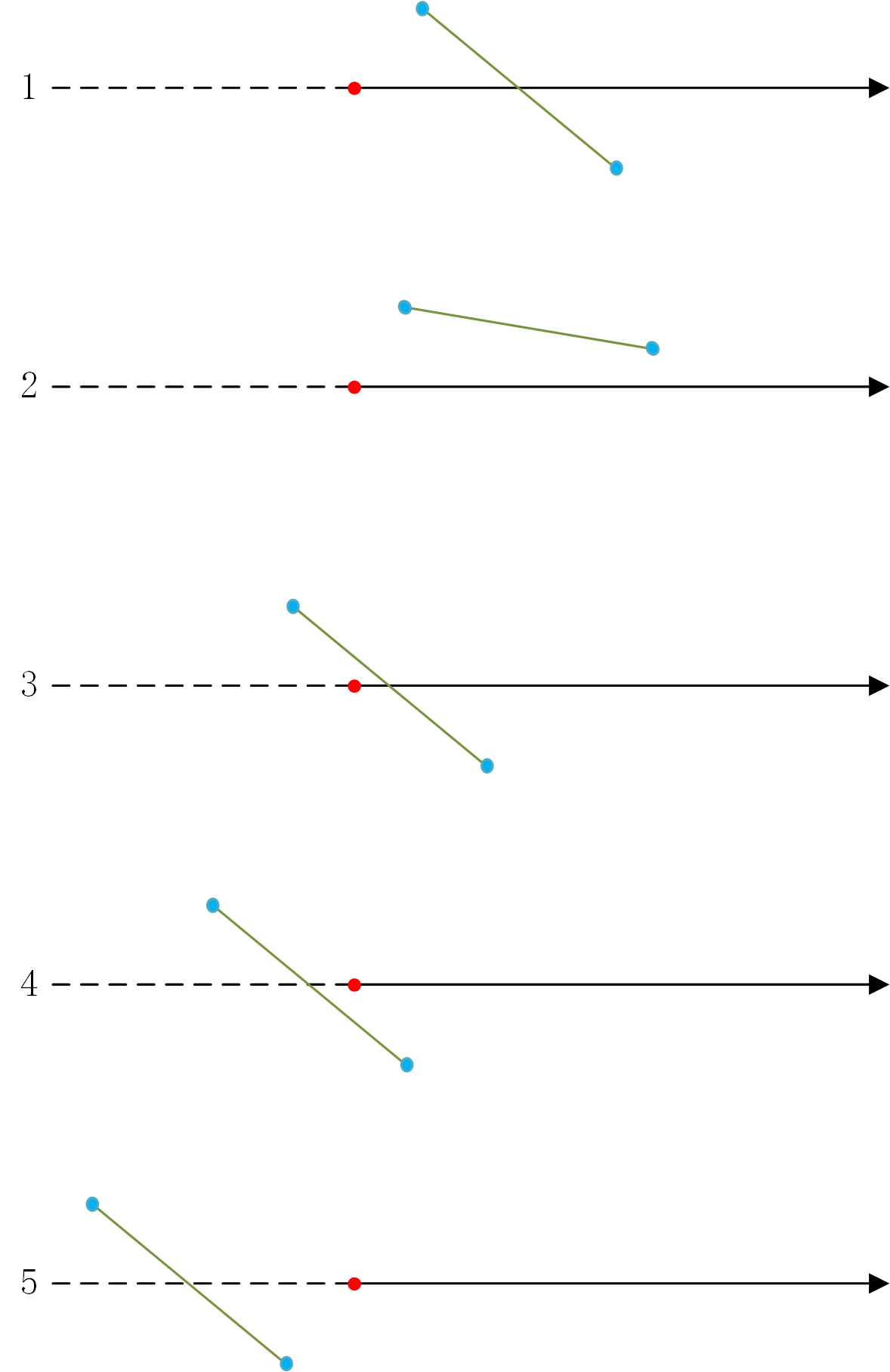
下面討論下一些特殊情況,如果所有點都是浮點數表示的話,那麽測試點和測試射綫恰好與多邊形頂點重合或相交概率是很小的,一般情況下不單獨考慮。但是儅點為整型時,這些情況需要精心設計處理,否則會得到錯誤的結果。
- 測試射綫恰好經過多邊形頂點時;
- 測試點恰好為多邊形的頂點;
- 測試射綫與多邊形一條或多條邊重合;
情況1處理方式: 論文中給處理意見是:無論射綫何時與頂點相交,都假設頂點在射綫上方無限小的位置。如下圖所示。這樣處理,相當於同時加、減兩個交點,并不改變交點個數的奇偶性。
情況2處理方式: 如果能判定測試點和多邊形頂點重合,那麽直接判定其在多邊形内即可;
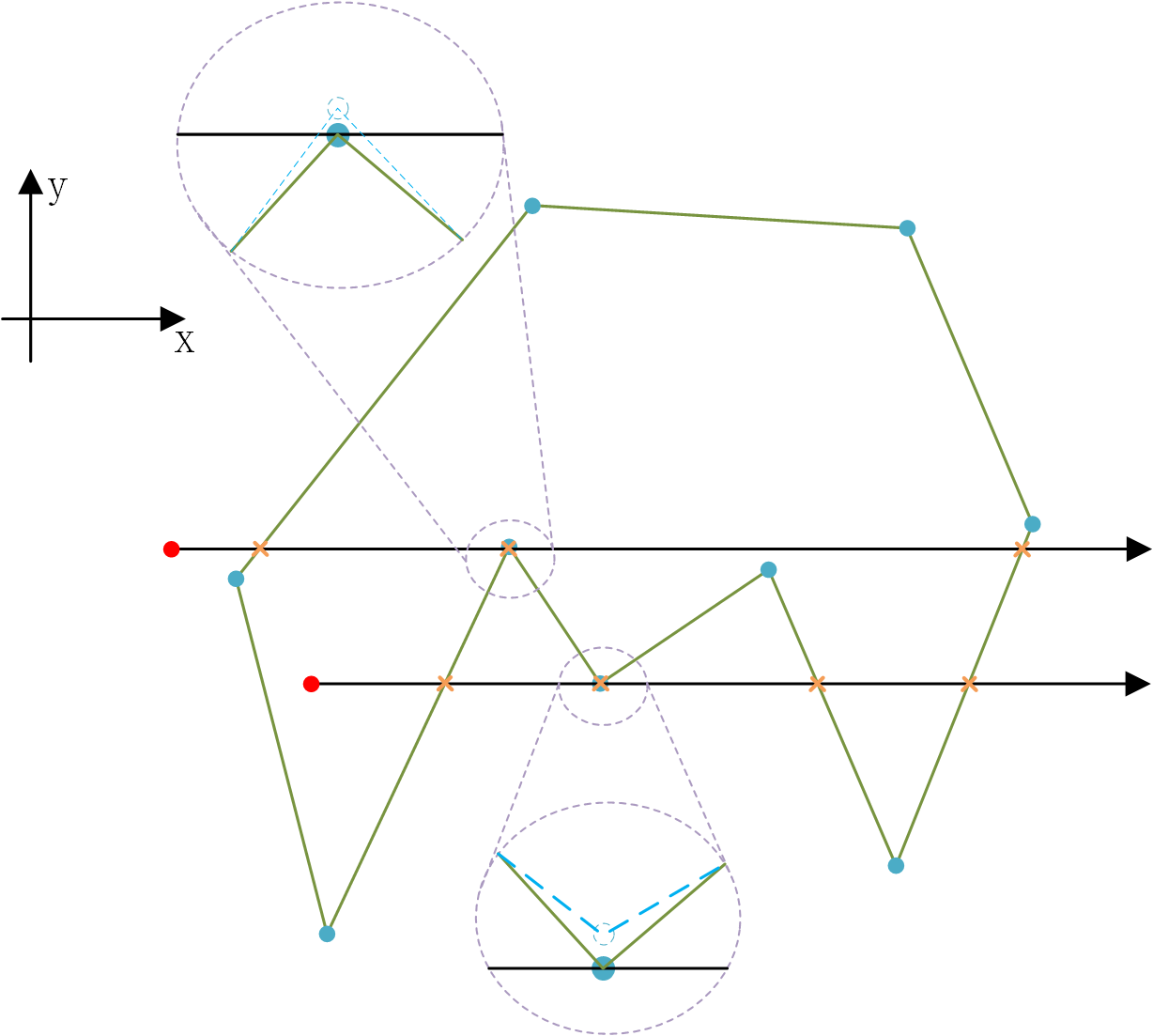
情況3處理方式: 下圖列舉了情況3的八種情況(A~H)。其中綠綫為多邊形的邊,藍色點為多邊形頂點,紅色點為測試點,黑色射綫為測試綫。
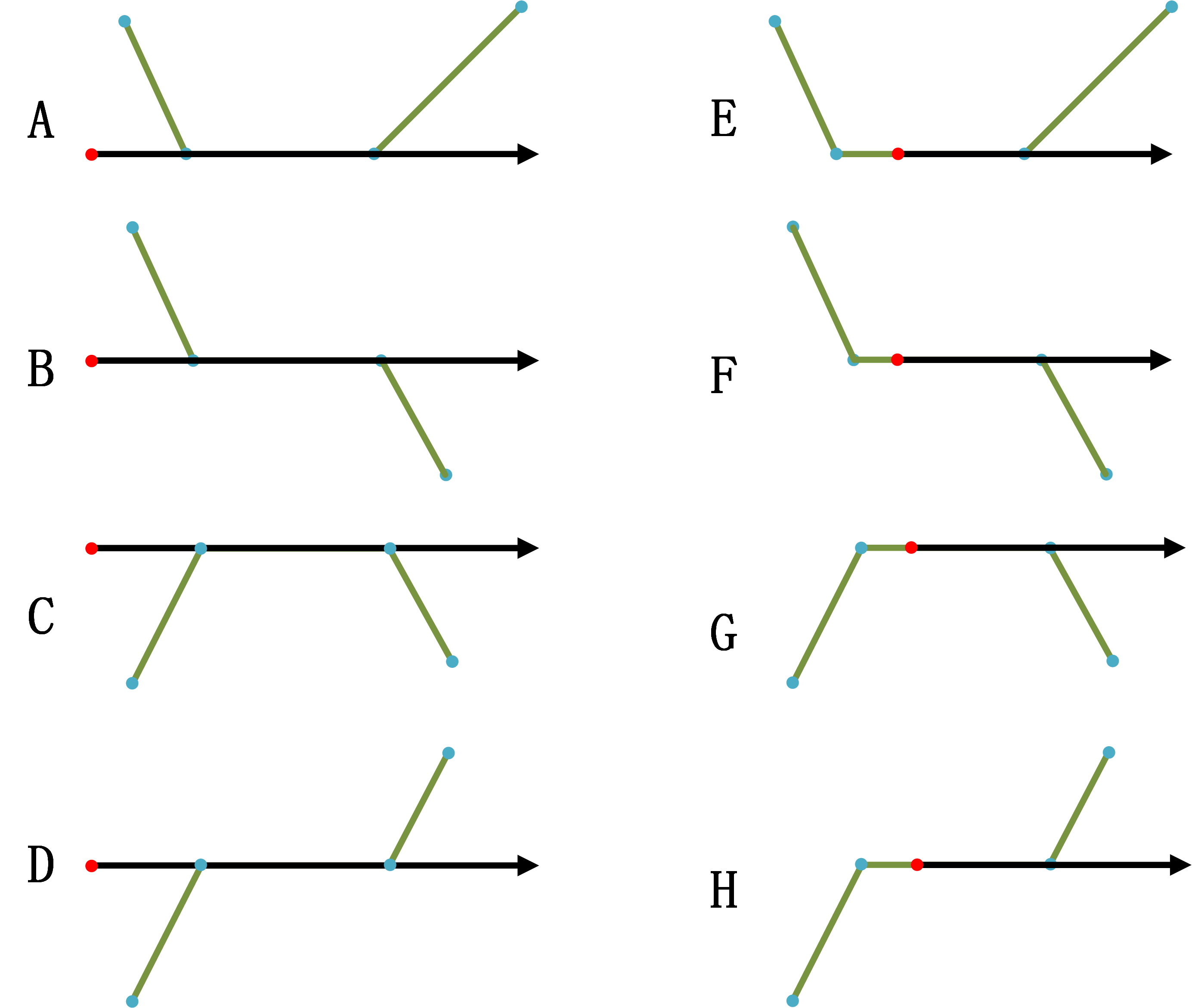
對於A~D四種樣式,我們可以將其退化成情況1 處理,即將水平邊看作一個多邊形頂點處理;但對於E~H四種樣式,若退化成情況1處理的話就會出錯,因此個人想法是類似情況2處理,如果判斷出其在一條多邊形邊上,直接返回點在多邊形内。
論文中crossing test代碼可以在Github中找到。
Winding Number
根據winding number介紹可知,我們只需以多邊形邊為運動軌跡,獲得測試點的winding number就能判斷點是否能落在多邊形内。這樣,winding number test就追蹤多邊形邊相對於測試綫,是從$Y+$平面到$Y-$平面(winding number $+1$),還是從$Y-$平面到$Y+$平面(winding number$-1$)。最後利用它的值判斷點是否在多邊形内。
而另一種更精確,但效率低的做法是纍加計算測試點與多邊形頂點連綫與$X$軸的夾角。如果纍加夾角趨近於$360^\circ$的倍數($0$除外),則説明點落在多邊形内;如果纍加夾角趨近為$0^\circ$,則點落在多邊形外。
由於計算角度會用到大量三角函數的調用,所以論文《An incremental angle point in polygon test》介紹了加速方法,有興趣可以自行詳細閲讀。但相比與crossing test而已,該方法效率依舊遜色不少。當然,仔細看的話,計算winding number與crossing test本質是一樣的,只是統計的東西不同而已,所以最終算法都可以用相同的方式實現(論文中提供的代碼也是這麽做的)。
Triangle Fan Test
該方法是將多邊形當作由多個三角形扇區構成的,利用三角形重心公式測試點是否落在多邊形内。所謂三角形重心坐標測試即滿足以下條件,則判斷點落在三角形内,其中$v_0、v_1、v_2$為三角形頂點:
對於凸多邊形,儅某個三角形與測試點重叠(即點在三角形内),測試即可終止,判定點落在該多邊形内;對於非凸多邊形(即任意多邊形),需要測試完所有三角形,然後統計點與三角形的重叠數,若該數為奇數,則點落在多邊形内,否則,點在多邊形外。
Half-Plane Test
重心測試在多邊形邊數量增多時,效率會顯著下降。如果預先歸一化重心公式,并且記錄預先計算的值,能獲得更好的性能。《Ray tracing News》中“Simple, Fast Triangle Intersection”提到了一個更快的測試方法,描述如下:
Store with each triangle $2$ indices, $i_1$ and $i_2$. These are the coordinate offsets for the two axes that will be considered in the test. (the axis with the largest component in the normal vector is dropped, as usual). Store the $2$ coefficients and the $1$ constant of the “inside-outside” equation of each edge.
To test for intersection, calculate $C[0]*X[i_1]+C[1]*X[i_2]+C[2]$ ($X$ is the intersection coordinate, and $C$ are the $3$ constants for the linear equation calculated at setup time) over all $3$ edges. If any of them have a negative (or positive depending upon which convention you choose) result, return NO_INTERSECTION.
其主要思路就是利用三角形三條邊的直綫方程,判斷測試點在這些方程的哪一側,如果都在同一側,則説明測試點落在三角形内;否則,測試點落在三角形外。
“Simple, Fast Triangle Intersection, part II”有對這一方法做了補充。他指出,三角形重心法本質也是一種Half-Plane Test,利用Half-Plane Test的一個額外好處是,其Half-Plane的高度是歸一化的,如下圖所示。

從上圖可以看出,$\Delta ABC$其實是由三個half-plane的交集(Half-Plane Test),或是三個雙界的交集(重心法)。所以,這兩者本質是一樣的,只是使用過程中,提前退出條件不同,對於Half-Plane Test,$\alpha < 0.0$爲其退出條件,而對於重心法的退出條件為:$\alpha < 0.0 $ 或$ \alpha > 1.0$。
Grid Method
該方法是一種時間複雜度低,而空間複雜度高的方法。該方法將多邊形的外包矩形(bounding box)劃分爲$m \times n$個cell,這些cell與多邊形的關係只有以下三種:完全在多邊形内、完全在多邊形外以及中間狀態。對於中間狀態,每個cell保存一個被多邊形重叠的邊緣列表,并且該cell有一個或多個角會落在多邊形内或多邊形外。最後我們通過查詢測試點落在哪個cell中,就可以知道該點是否落在多邊形内。
根據該方法的描述可以知道,該方法之所以快,是因爲它本質只是查表操作,但對於查表操作是需要一定的預處理操作的。對於多邊形而言,大多數cell的狀態要麽完全落在多邊形内,要麽完全落在多邊形外,因此對於包含多邊形邊界的cell,只需要檢查測試點與cell的角的連綫是否與該cell中邊界列表相交次數即可。
需要注意的是,儅選擇cell尺度不理想時,會導致多邊形恰好(或幾乎完全)經過cell的角,此時該角是無法分類的。與其處理拓撲結構和數值精度問題,一種更簡單有效的方法是換個尺度重新對bounding box進行劃分並計算cell分類。此外,儅測試綫段與邊緣列表相交時,邊緣端點的精確交點只能統計一次。
還有一個額外的方式對該問題進行改進。每個cell有四條邊,如果其中一條邊沒有與多邊形任意邊界相交,那麽該邊要麽完全落在多邊形内,要麽完全落在多邊形外。從測試點相該cell邊引出水平或垂直的測試綫段,利用快速相交測試判定與該cell内的多邊形邊界相交情況。值得一提的是,相交測試對於端點的相交是具有魯棒性的。
論文中Grid Test代碼可以在Github中找到。
Pixel Based Testing
Grid Method的一個極端做法就是將cell退化成像素尺寸,儅多邊形在圖像上顯示時,我們構建一個與圖像相同的空間,該空間用於記錄每個像素與多邊形的關係。那麽在進行測試點判斷時,也只需要進行查詢就能獲得結果。
Convex Polygons
對於凸多邊形,由於其幾何性質,在判定時能夠做的更快。例如,利用相交測試時,儅檢測到兩次$Y$值符號變化即可停止,因爲凸多邊形的性質決定了$Y$值符號變化最多為兩次。對於triangle fan test,同樣只要檢測到點在其中一個三角形内即可退出。
儅利用half-plane方式判斷點是否落在凸多邊形内,通常只要判定點是否落在任意邊界外。這個算法相比於triangle fan test不需要額外的存儲空間,而且代碼簡單明瞭。但是該算法速度受到测试邊緣順序的影響,截斷多邊形所在bounding box越多區域的邊緣越早被測試越好。但是要找到最優的順序是很困難的,而按順序測試邊緣這一策略同樣糟糕。隨機化邊緣順序可以使得該算法對於一般多邊形整體性能有$10%$的提升。
Hybird Half-Plane
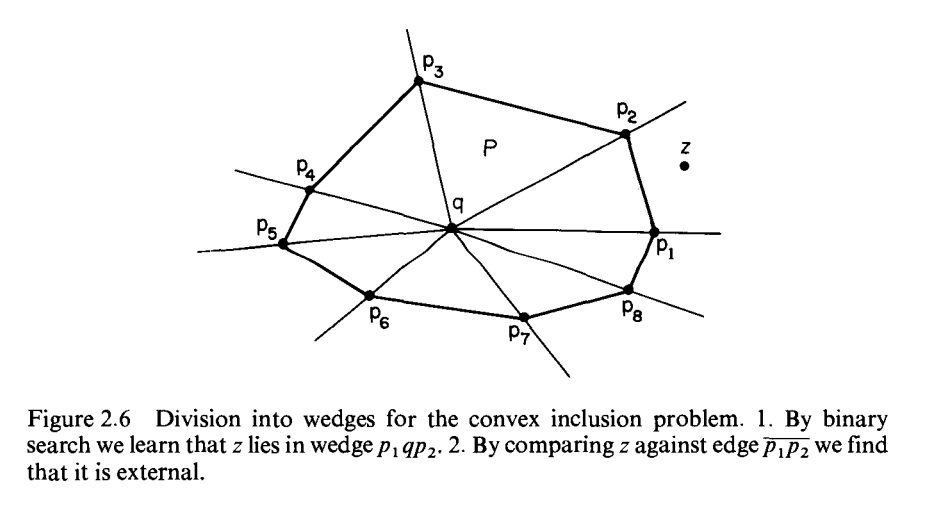
《Computational Geometry: An Introduction》中提到一種測試方式,其時間複雜度為$O(logN)$,空間複雜度為$O(N)$,預處理複雜度為$O(N)$。具體做法是,在凸多邊形内部添加一個中點,該中點與多邊形頂點的連綫稱爲wedge,選定其中一條wedge為錨定邊(anchor edge),從該邊出發,利用二分查找找到測試點落在哪兩條wedge之間,再利用half-plane方式判斷點落在多邊形内還是多邊形外。如下圖所示。
Statistics
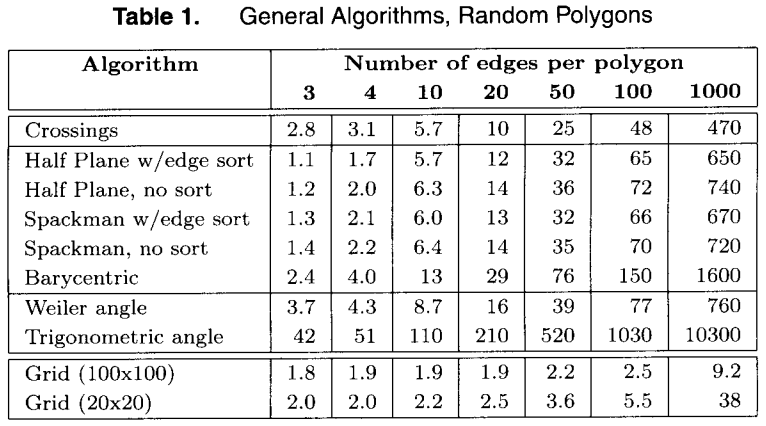
下面三圖為論文中提及的各種算法對比,具體耗時請自行在目標機器上測試,圖中只展示不同算法閒的差別。
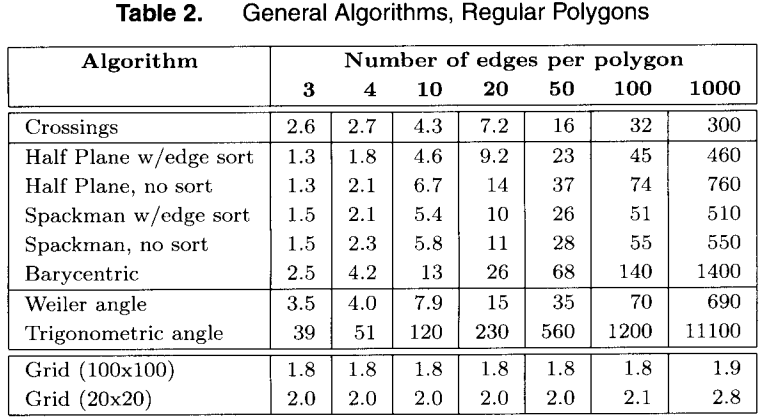
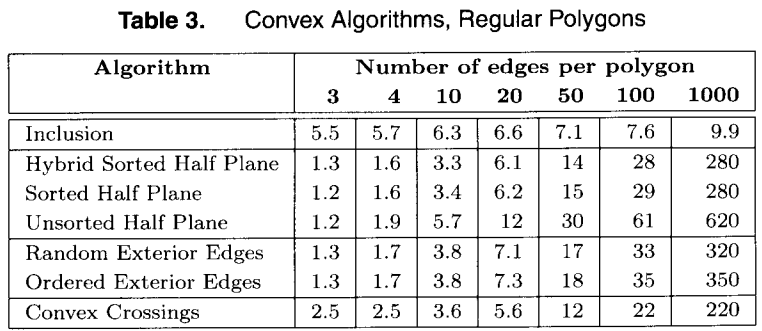
Conclusions
論文中總結了各類算法的適用場景。
- 如果沒有額外的存儲空間或不能進行預處理,則使用
Crossing Test方法; - 如果能有少量額外存儲空間,并能進行一定預處理:
- 對於任意多邊形
- 多邊形邊數較少,使用
Half-Plane或Spackman方法; - 多邊形邊數較多,使用
Crossing Test方法;
- 多邊形邊數較少,使用
- 對於凸多邊形
- 多邊形邊數較少,使用
Hybrid Half-Plane方法; - 多邊形邊數較多,使用
Inclusion方法; - 但是,如果$\frac{\text{bounding box}}{\text{polygon}}$比例較高,使用
Exterior Edges方法;
- 多邊形邊數較少,使用
- 對於任意多邊形
- 如果允許進行預處理,并且存儲空間充足,則使用
Grid Test方法(除了三角形外)。
這些總結不是一定的,還需要根據自身機器架構和編譯器優化進行調整,換而言之,沒有最好的算法,挑選合適自身需求的就行。
Code
作者代碼發佈在Github上,可自行下載學習。
References
[1] Point in Polygon Strategies
[2] Simple, Fast Triangle Intersection
[3] Simple, Fast Triangle Intersection, part II
[4] C-Code