該論文介紹了實現高性能矩陣乘法的基本準則。

1. Introduction

實現高性能矩陣乘法，需要瞭解在宏觀層面如何對操作進行分層，并在微觀層面仔細設計高性能内核。本文主要解決宏觀問題，即如何設計高性能内核，而不是微觀層面的工程問題。

在論文[Gunnels et al. 2001][1]中，利用分層技術實現了矩陣相乘的運算。這個方法被證明，對於複雜的、多級内存結構而已，能夠最大的分攤相鄰層級閒數據移動的損耗（即效率上的損失）。與該領域其他工作類似，論文[Gunnels et al. 2001]計算矩陣的方式同樣為$C = \tilde{A}B + C$。其中， 矩陣$\tilde{A}_{m_c \times k_c}$是連續存儲在合適的緩存中。但是該論文[Gunnels et al. 2001]中使用的内存層級模型至少有兩方面是不切實際的：

  • 假設計算時，矩陣$\tilde{A}$始終在L1級緩存中;
  • 忽略了TLB(Translation Look-aside Buffer)的使用。

在相關技術報告[Goto and van de Geijn 2002][2]中指出：

  • 浮點運算器的計算效率，即flops(floating point operations)，低於浮點數從L2級緩存流入寄存器的效率。這就意味著矩陣$\tilde{A}$能夠存放在L2級緩存中。
  • TLB能夠處理的數據量影響矩陣$\tilde{A}$的尺寸。

另外，還發現：

  • 事實上，有六個内核應該被考慮構建高性能矩陣乘法模塊，其中之一被認爲遠優於其他。論文[Gunnels et al. 2001]中只確認了其中的三個。

論文結構安排如下：

  • Section 2介紹論文中使用的符號標記；
  • Section 3介紹矩陣相乘的分層方法；
  • Section 4介紹高性能實現的内核；
  • Section 5給出最常用的矩陣相乘算法；
  • Section 6給出更多細節，這些細節用於知道調整參數，以達到最佳性能；
  • Section 7介紹各種架構在最佳優化結果下的性能表現；
  • Section 8給出結論性評價。

2. Notation

對於任意$m \times n$矩陣$\mathbf{X}$，都可以將其按行或列拆分成block，其中$m$表示行數，$n$表示列數。

$$ \mathbf{X}_{m\times n} = (\mathbf{X}_0 | \mathbf{X}_1 | \cdots | \mathbf{X}_{N-1} ) = \begin{pmatrix} \hat{\mathbf{X}}_0\\ \hat{\mathbf{X}}_1\\ \vdots \\ \hat{\mathbf{X}}_{M-1} \end{pmatrix} $$

因此，根據矩陣不同的拆分組合，定義其名稱，如下。

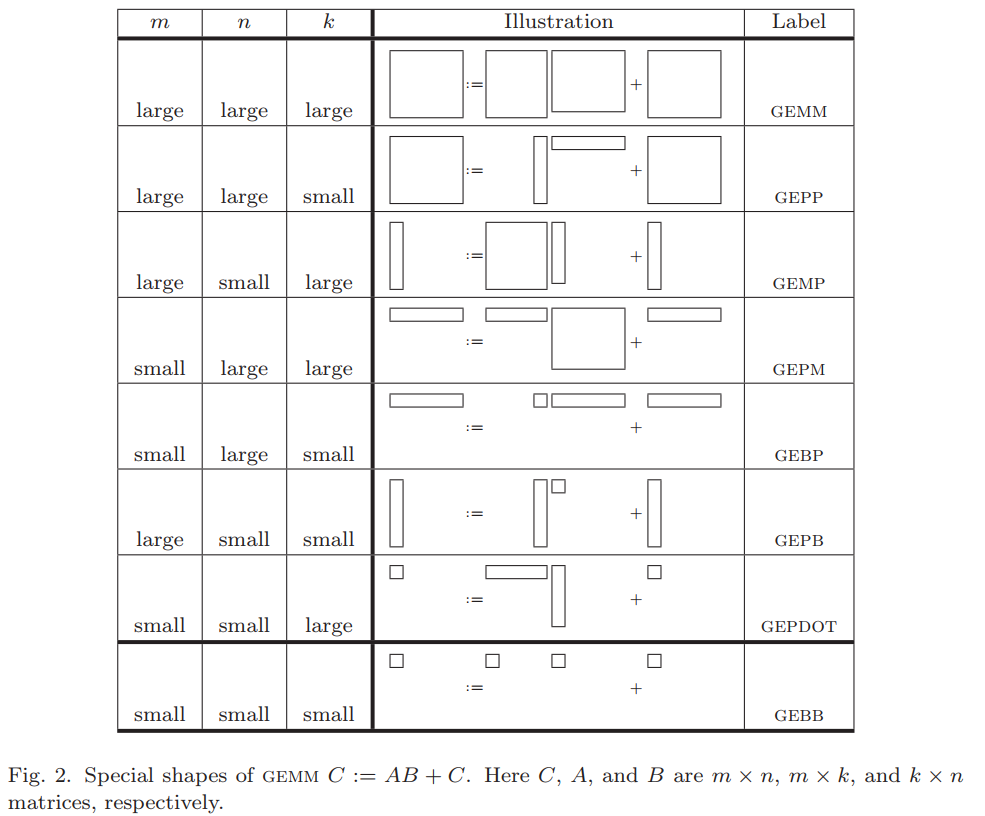
名稱中，不同字母代表的含義如下。

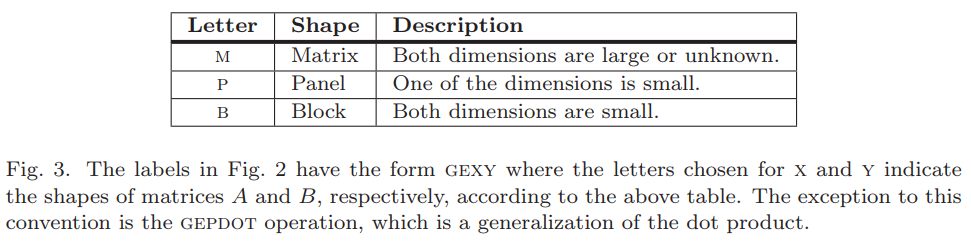
3. A LAYERED APPROACH TO GEMM

對於任意兩個矩陣相乘，都可以成爲GEMM（即，General Matrix Multiplication）。它們都可以按下面的方式拆分成三种不同的子模块相乘：GEBP、GEPB和GEPDOT。

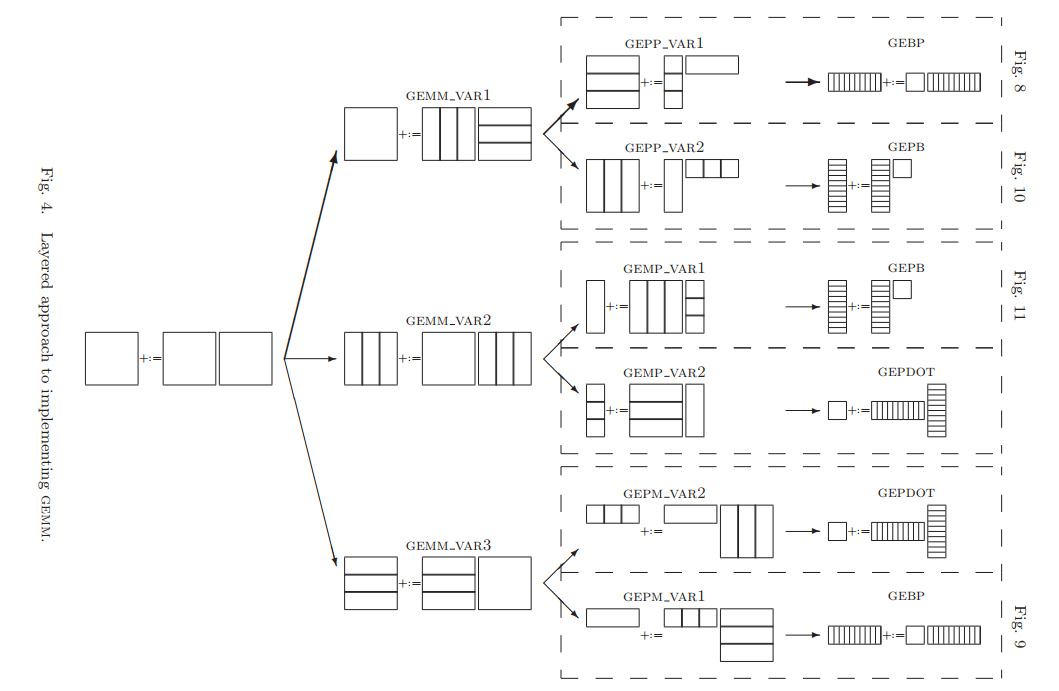
下圖展示了標準三重循環體計算矩陣乘法中，不同層循環對應的子模塊。

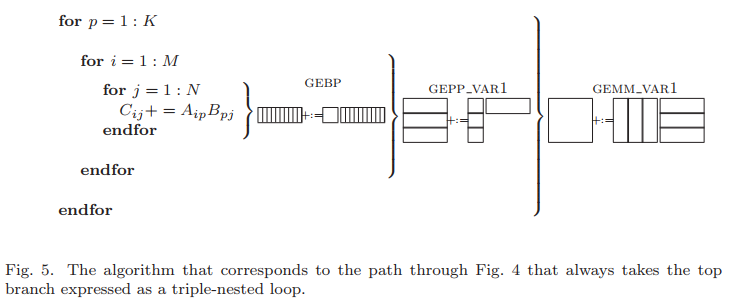
這裏再定義子矩陣符號。

$$ \mathbf{C} = \begin{pmatrix} C_{11} & \cdots & C_{1N}\\ \vdots & & \vdots \\ C_{M1} & \cdots & C_{MN} \end{pmatrix}, \mathbf{A} = \begin{pmatrix} A_{11} & \cdots & A_{1K}\\ \vdots & & \vdots \\ A_{M1} & \cdots & A_{MK} \end{pmatrix}, \mathbf{B} = \begin{pmatrix} B_{11} & \cdots & B_{1N}\\ \vdots & & \vdots \\ B_{K1} & \cdots & B_{KN} \end{pmatrix} $$

其中，

$$ \mathbf{C}_{ij} \in \mathbb{R}^{m_c \times n_r} \ , \mathbf{A}_{ip} \in \mathbb{R}^{m_c \times k_c}\ , \mathbf{B}_{pj} \in \mathbb{R}^{k_c \times n_r} $$

這裏$m_c$、$n_r$和$k_c$子塊尺寸，在之後優化過程中有重要作用。

4. HIGH-PERFORMANCE GEBP, GEPB, AND GEPDOT

既然矩陣乘法能夠拆分成幾個子任務執行，那麽子任務的效率直接影響矩陣乘法的效率。本節就分別對這三種子模塊性能進行分析。

4.1 basic

下來討論數據在存儲介質中移動的效率。下圖為多級存儲介質的抽象模型。

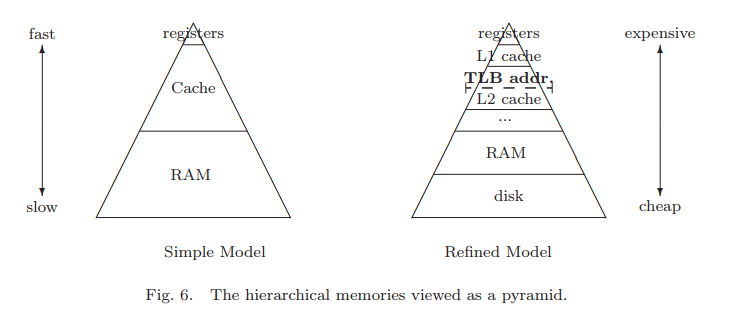
程序在運行過程中，基本都會使用寄存器，這玩意速度快，數量少，造價高；而要處理的數據一般會在内存，也就是RAM，或硬盤中，這兩者之間速度差距非常非常非常大，爲了彌補這兩者閒差距，引入Cache，也就是緩存。雖然緩存造價也高，但相比寄存器，其數量可以做到KB級或是MB級，而且其速度與寄存器相差并不是太大。這樣就能得出一個優化方向，如果處理數據能夠都放在Cache中，那麽效率就能非常高，所以之後所有優化手段就是盡可能將Cache有效利用。

下面先對GEBP子模塊進行討論。 假設，其子矩陣為： $\mathbf{C} \in \mathbb{R}^{m_c \times n}$，$\mathbf{A} \in \mathbb{R}^{m_c \times k_c}$和$\mathbf{B} \in \mathbb{R}^{k_c \times n}$。其中矩陣$\mathbf{B}$及$\mathbf{C}$又可繼續分爲寬度為$n_r$的列向量形式。

$$ \mathbf{B} = \begin{pmatrix} \mathbf{B}_0 | \mathbf{B}_1 | \cdots | \mathbf{B}_{n-1} \end{pmatrix} \ \ and \ \ \mathbf{C} = \begin{pmatrix} \mathbf{C}_0 | \mathbf{C}_1 | \cdots | \mathbf{C}_{n-1} \end{pmatrix} $$

此時做如下假設： (a). $m_c$和$k_c$足夠小，可以使子矩陣$\mathbf{A}$和寬度為$n_r$的矩陣$\mathbf{B}_j$和$\mathbf{C}_j$都能夠放到cache中； (b). 如果$\mathbf{A}$、$\mathbf{B}_j$和$\mathbf{C}_j$都放在cache中，則CPU利用率達到峰值； (c). 矩陣$\mathbf{A}$直到不再需要使用時才從cache中移除。

基於這三個假設，得到算法僞代碼如下。

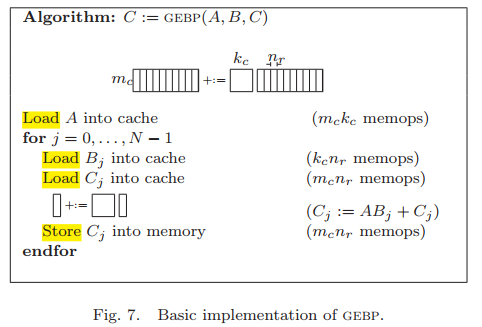
分析，在這個算法中，數據在存儲介質中的移動量memops為：

$$ m_ck_c + \sum_{j=1}^{N-1}(k_cn_r+m_cn_r+m_cn_r) = m_ck_c + (2m_c + k_c)n $$

另外浮點運算量為：$\mathrm{2m_{c}k_{c}n} flops$，兩者比值為：

$$ \mathrm{\frac{2m_{c}k_{c}n}{m_{c}k_{c} + (2m_{c} + k_{c})n}}\frac{flops}{memops} \approx \mathrm{\frac{2m_{c}k_{c}n}{(2m_{c} + k_{c})n}}\frac{flops}{memops}\ \ when \ \ k_c << n \tag{1} $$

這個比值的含義是，每單位數據移動開銷可以換來多少浮點運算性能。因此，在前面三個假設(a)~(c)以及盡可能數據盡可能占滿cache的約束下，盡量使下面式子最大化 $$ \frac{2m_ck_c}{2m_c + k_c}\tag{2} $$

對於另外兩種子模塊，也可采用這樣的方式進行分析。

同理可得GEPB的移動量memops為：

$$ k_cn_c + \sum_{j=1}^{M-1}(m_rk_c + m_rn_c + m_rn_c) = k_cn_c + (2n_c+k_c)m $$

GEPB的浮點運算量為：$\mathrm{2mk_{c}n_{c}} flops$，兩者比值為：

$$ \mathrm{\frac{2k_{c}n_{c}m}{k_{c}n_{c} + (2n_{c} + k_{c})m}}\frac{flops}{memops} \approx \mathrm{\frac{2n_{c}k_{c}m}{(2n_{c} + k_{c})m}}\frac{flops}{memops}\ \ when \ \ k_c << m $$

GEPDOT的移動量memops為：

$$ m_cn_c + \sum_{i = 1}^{K-1}(m_ck_r + \sum_{j=1}^{K-1}n_ck_r) = m_cn_c + (m_ck + K\cdot kn_c) = m_cn_c + (m_c + K\cdot n_c)k $$

GEPDOT的浮點運算量為：$\mathrm{2m_{c}n_{c}k} flops$，兩者比值為：

$$ \mathrm{\frac{2m_{c}n_{c}k}{m_{c}n_{c} + (K\cdot n_{c} + m_{c})k}}\frac{flops}{memops} \approx \mathrm{\frac{2m_{c}n_{c}k}{(K \cdot n_{c} + m_{c})k}}\frac{flops}{memops}\ \ when \ \ n_c << k $$

4.2 Refinements

下面繼續深入探討GEBP的優化。現假設矩陣的存儲方式為“列主序”的方式。

4.2.1 Choosing the cache layer

通過圖6可以知道，存儲器是有等級劃分的！！！在Cache中，又細分爲了L1-cache，L2-cache等，那麽第一個問題就是，子矩陣$\mathbf{A} \in \mathbb{R}^{m_c\times k_c}$ 應該放在哪一級的cache中？

根據等式(2)以及假設條件(a)~(c)可知，$m_c \times k_c$越大，在RAM與Cache之間數據移動的開銷將在計算過程中被分攤的效果越好。這就推出可將矩陣$\mathbf{A}$放到遠離寄存器的Cache中。

如果放在L1-cache中，由於它比較小，所以不太合適；那麽如果放在L2-cache中呢？

令$R_{comp}$表示CPU運算浮點操作的速率；$R_{load}$表示浮點數從L2-cache到寄存器中的速率。假設矩陣$\mathbf{A}$放在L2-cache中，矩陣$\mathbf{B}_j$和$\mathbf{C}_j$放在L1-cache中，忽略L1-cache到寄存器的性能損失。那麽，計算$\mathbf{A}\mathbf{B}_j +\mathbf{C}_j$時，計算量為$2m_ck_cn_r$，數據移動量為$m_ck_c$，即矩陣$\mathbf{A}$從L2-cache到寄存器。因此，兩者效率需滿足下面的關係才能達到優化的目的。

$$ \begin{align} \frac{2m_ck_cn_r}{R_{comp}} &\geq \frac{m_ck_c}{R_{load}} \\[2ex] \Rightarrow \frac{2n_r}{R_{comp}} &\geq \frac{1}{R_{load}} \\[2ex] \Rightarrow n_r &\geq \frac{R_{comp}}{2R_{load}}\tag{3} \end{align} $$

4.2.2 TLB considerations

接下來考慮的是“頁管理系統”。現代模型中使用了虛擬内存的概念，即它的大小不受物理内存大小限制。管理這些虛擬内存的方式是將其劃分成$N$份預設大小的頁，之後有一個表，記錄這些頁與物理内存的映射關係。這個方式的一個問題是，該映射表也是存放在内存中的，從其映射到物理内存也是需要開銷的。爲了剋服這個問題，引入一個更小、轉換效率更高的映射表，TLB（Translation Look-aside Buffer），它保存了經常使用的頁信息。

下面説説TLB miss，儅虛擬内存地址在TLB中查詢不到時，發生TLB miss，此時將查詢條目從page table中移到TLB table中。換而言之，TLB相當於page table的cache。

cache miss和TLB miss的區別在於，cache miss不會導致CPU停頓。可以使用預取數據的方式來一定程度上規避cache miss，而TLB miss不行。

由於現代架構中TLB的存在，現在引入兩個新的假設：

(d). 維度為$m_c，k_c$足夠小，子矩陣$\mathbf{A}$，$n_r$列矩陣$\mathbf{B}_j$以及$n_r$列矩陣$\mathbf{C}_j$都能通過TLB映射到，并且在計算過程中不會發生TLB miss。

(e). 矩陣$\mathbf{A}$一直放在TLB映射表中，直到不需要爲止。

4.2.3 Packing

由於矩陣$\mathbf{A}$是子矩陣，所以在存儲上它是不連續的，這意味著尋址次數會比TLB條目多得多。解決這個問題的方法是Packing，將不連續的子矩陣$\mathbf{A}$打包成連續的矩陣$\tilde{\mathbf{A}}$。這樣，選擇合適的$m_c$、$k_c$參數就能讓$\tilde{\mathbf{A}}$，$\mathbf{B}_j$和$\mathbf{C}_j$都能放入L2-cache中並且都能被TLB查詢到。

Case 1： TLB為約束條件。

假設，總共有$T$條TLB條目，矩陣$\tilde{\mathbf{A}}$，$\mathbf{B}_j$和$\mathbf{C}_j$的TLB條目分別爲$T_{\tilde{A}}$，$T_{B_{j}}$和$T_{C_j}$，那麽它們必須滿足下面條件。

$$ T_{\tilde{A}} + 2(T_{B_j} + T_{C_j}) \leq T $$

爲什麽會有因子$2$，因爲TLB條碼更新的機制是替換時間最早的未使用條目。那麽這裏$\tilde{\mathbf{A}}$是最先讀取的，接著是$\mathbf{B}_j$和$\mathbf{C}_j$，儅完成$C_j = \tilde{A}B_j + C_j$，讀取新的$\mathbf{B}_{j+1}$和$\mathbf{C}_{j+1}$時，有可能將最早的$\tilde{\mathbf{A}}$條目替換掉，這就違背了假設(e)。因此，我們只需要增加一倍$T_{B_j}$和$T_{C_j}$就能規避這個問題。因爲，$\mathbf{B}_{j+1}$和$\mathbf{C}_{j+1}$不需要替換任何之前條目就能放入TLB表中，但當讀取$\mathbf{B}_{j+2}$和$\mathbf{C}_{j+2}$時，$\mathbf{B}_{j}$和$\mathbf{C}_j$條目成爲最早的未使用條目。

Case 2：L2-cache尺寸為約束條件。

這裏沒有詳細展開。

4.2.4 Accessing data contiguously

不僅數據存放是連續，還要對數據進行重新排列，這樣保證計算過程數據讀取也是連續。

4.2.5 Implementation of GEPB and GEPDOT

这两种方式的分析方式同GEBP。

5. Practical Algorithms

本節對圖4中六個拆分方式的算法進行分析。

5.1 Implementing GEPP with GEBP

算法僞代碼如下：

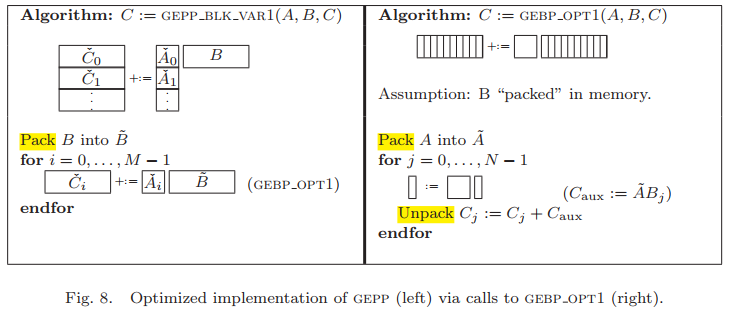
假設TLB縂條目為$T$，根據GEBP_OPT1可知，$\mathbf{B}_j$使用1條TLB條目，$\mathbf{B}_{j+1}$使用1條，$\mathbf{C}_{aux}$使用1條，在Unpacking過程中，需要使用$n_r$條$\mathbf{C}_j$的TLB條目，因此，$T_{\tilde{A}} \leq T-(n_r+3)$。

對$\mathbf{B}$的packing操作，其是内存閒拷貝，開銷與$k_c \times n$成正比，且分攤到$2m \times n \times k_c$次運算中。這個packing操作會破壞TLB之前的内容。

對於$\mathbf{A}$的packing操作，其需要精心設計並重排，使其可保留在L2-cache中，其開銷正比於$m_c \times k_c$，也可分攤到$2m_c \times k_c \times n$次計算中去。這個拷貝工作是相對“廉價”的。

5.2 Implementing GEPM with GEBP

GEBP計算的另一種形式。

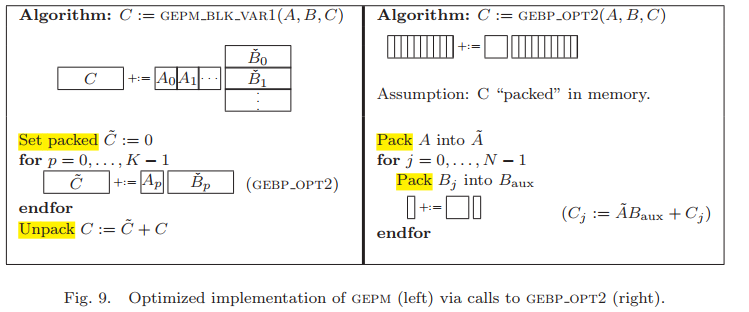
這個形式中，矩陣$\mathbf{C}$需要重複更新，而$\tilde{\mathbf{B}}_p$沒有重複使用，因此其也不需要packing，這樣TLB條目數也可計算出，$n_r$條$\mathbf{B}_j$的，1條$\mathbf{B}_{temp}$，1條$\mathbf{C}_j$以及1條$\mathbf{C}_{j+1}$的，這樣$T_{\tilde{A}} \leq T-(n_r + 3)$。

5.3 Implementing GEPP with GEPB

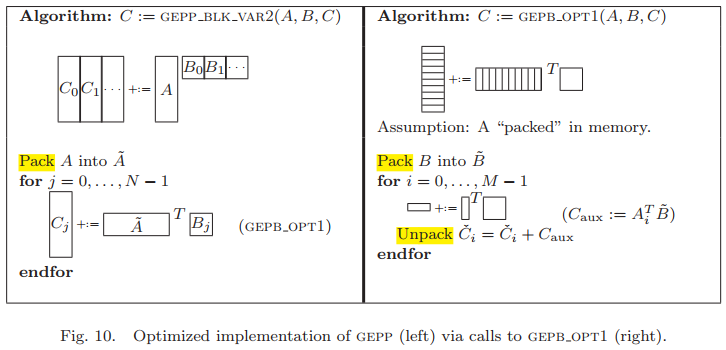
此時需要將$\mathbf{B}$打包、保留在L2-cache中。同理可知，$T_{\tilde{B}}$需要最大化，而$\mathbf{A}_i$、$\mathbf{A}_{j+1}$和$\mathbf{C}_{aux}$各使用一條TLB條目，因此$T_{\tilde{B}} \leq T - (n_c + 3)$。

5.4 Implementing GEMP with GEPB

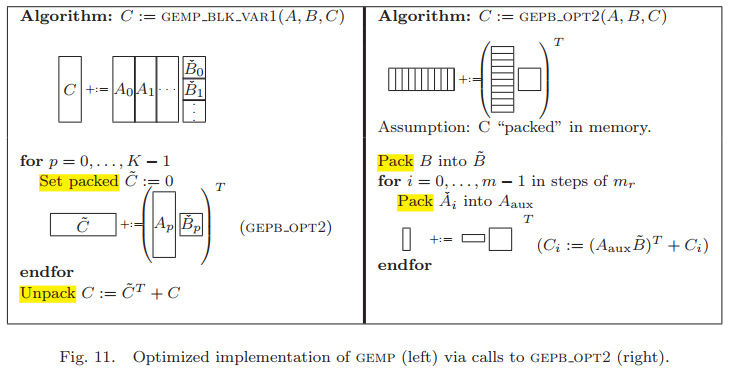
與5.3類似，$T_{\tilde{B}}$需要最大化，而$\mathbf{C}_i$、$\mathbf{C}_{i+1}$和$\mathbf{A}_{temp}$各使用一條TLB條目，因此$T_{\tilde{B}} \leq T - (m_c + 3)$。

5.5 Implementing GEPM and GEMP with GEPDOT

GEPDOT拆分方式不是一個好的優化方向，所以這裏不多做介紹。下面一節中會給出其爲什麽不好的原因。

5.6 Discussion

對於列主序存儲的矩陣，圖8的拆分方式優先考慮。

首先，先關注L2-cache與寄存器之間帶寬問題。基於GEPDOT的方式相較於GEBP或GEPB的方式，需要2倍的帶寬實現從L2-cache和寄存器之間的通信，這也導致其性能不好。

接著對比同是GEBP，但其前置拆分方式不同的情況。比較圖8和圖9，圖8中是打包矩陣$\mathbf{B}$，將矩陣$\mathbf{C}$在内存中傳輸；圖9則是將矩陣$\mathbf{B}$在内存中傳輸，而計算矩陣$\mathbf{C}$時使用緩衝區，最後將緩衝區結果加到矩陣$\mathbf{C}$中。兩者效率上的差別在於，圖8將矩陣$\mathbf{C}$在内存中的移動開銷隱藏，只考慮矩陣$\mathbf{B}$packing的開銷；而圖9則是將矩陣$\mathbf{B}$在内存中的移動開銷隱藏，只考慮矩陣$\mathbf{C}$ unpacking的開銷。但是，矩陣$\mathbf{C}$的unpacking操作相比于packing矩陣$\mathbf{B}$要更複雜，所以圖8要優於圖9。同理可知，圖10相較於圖11的效率更優。

最後對比圖8和圖10，圖8對於列主序存儲更有優勢，而對於行主序則是圖10更有優勢。

6. More Details Yet

以图8中GEBP_OPT1爲例，深入分析寄存器在計算過程中的使用情況，并在之后给出各个参数如何选择。

下圖為該算法對應的矩陣模型。

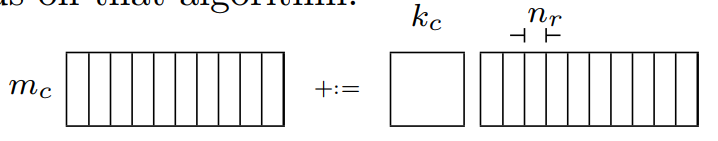
6.1 Register blocking

考虑其中$C_{aux} = \tilde{A}B_j$，其细分计算模型如下：

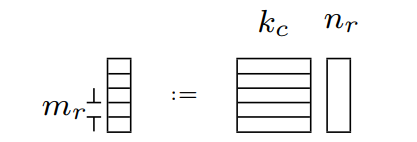
根據之前的分析，以及存儲模型的特性可知，$\tilde{A}$和$B_j$分別位於L2和L1緩存中。這樣對於$C_{aux}$中的子矩陣$m_r \times n_r$，可以利用寄存器進行運算，這就意味著在計算$C_j$時，其子矩陣元素不必常駐與L1緩存甚至是L2緩存中，因爲從寄存器可以將數據移動到存儲模型的任意一層結構中。因此對於這個子矩陣的浮點運算量為$\mathrm{2m_{r}n_{r}k_{c}} \ flops$，其數據移動量為$\mathrm{m_{r}n_{r}} \ memops$。

接著，再討論packing$A$到$\tilde{A}$的操作。對於$\tilde{A}$中每個$m_r \times k_c$子矩陣，其在内存中是連續的，且是按列主序存儲，這保證在計算時，$\tilde{A}$中元素能在連續内存中快速訪問到。

6.2 Choosing $m_r \times n_r$

以下三條$m_r \times n_r$選擇時需要考慮的影響：

  • 通常會使用一半的可用寄存器存儲$m_r \times n_r$子矩陣，剩餘寄存器用於預取$\tilde{A}$和$\tilde{B}$的元素；
  • 儅$m_r \approx n_r$時，分攤寄存器的數據載入開銷的效果是最佳的；
  • 如4.2.1小節中提到，將$\tilde{A}$中元素從L2緩存取到寄存器的時間不能長於前一個元素計算的時間，因此在理想情況下，$n_r \geq \frac{R_{comp}}{2R_{load}}$必須滿足。$R_{comp}$通常單位為$\frac{flops}{cycle}$，$R_{load}$通常是指Sustained Bandwidth。

這樣寄存器短缺會影響GEBP_OPT1能達到的最佳性能。

6.3 Choosing $k_c$

爲了分攤更新$C_j$中$m_r \times n_r$元素的開銷，$k_c$應該盡可能的大。但是其同樣有約束條件：

  • 由於$B_j$會被重複使用，其會常駐L1緩存中，但是集合關聯性和緩存替換策略又限制了$B_j$能夠占用多少L1緩存。這樣在實踐中，$k_cn_r$個浮點數應占用不到L1緩存一半的空間，這樣避免了$B_j$中的元素被$\tilde{A}$和$C_{aux}$驅逐。
  • $\tilde{A}$中$m_c \times k_c$個浮點數應占用L2緩存中大部分空間；

經驗選擇是，$k_c$使雙精度浮點數佔頁空間的一半。

6.4 Choosing $m_c$

受到L2緩存的集合關聯性和緩存替換策略的約束，通常選擇$m_c$使$\tilde{A}_{m_c \times k_c}$占據TLB可尋址内存和L2緩存中較小者的一半。

7. Experiments

這部分沒有認真看，都是不同設備上的測試結果和對比，不寫了。

8. Conclusion

作者對影響高性能矩陣乘法的高級問題進行了系統分析，這些見解被整合到一個算法實現中，并在各個平臺中獲得了極高的性能。

REFERENCES

[1]: Gunnels, J. A., Henry, G. M., and van de Geijn, R. A. 2001. A family of high-performance matrix multiplication algorithms. In Computational Science - ICCS 2001, Part I, V. N. Alexan-drov, J. J. Dongarra, B. A. Juliano, R. S. Renner, and C. K. Tan, Eds. Lecture Notes in Computer Science 2073. Springer-Verlag, 51–60.

[2]: Goto, Kazushige, and Robert van De Geijn. On reducing TLB misses in matrix multiplication. Technical Report TR02-55, Department of Computer Sciences, U. of Texas at Austin, 2002.