本文内容為個人做Games101課程作業-5時遇到問題的一個記錄，主要為説明作業中如何生成一條Primary Ray或Camera Ray。不知道作業5是什麽内容的請移步此鏈接。不想看我廢話的，請直接關閉或移步Scratchapixel-Generating Camera Rays。遵守Games101課中閆老師的要求，本文不會提供作業5的代碼框架，只會提供公式推導及代碼實現片段。另外説明，本文只是個人學習過程中一些淺薄理解，如果問題請郵件聯係討論或在下方留言，郵箱地址uninitmatrix@gmail.com。

解題初始思路

作業5的要求很簡單：

  1. 生成camera rays；
  2. 判斷camera rays是否與三角形網格相交。

剛看完題目感覺好簡單啊，不就是從人眼透過圖像上每個像素“發出”光綫，然後判斷光綫與三角形網格中每個三角形進行相交測試，都是老師課中講過的知識。但是開始實現時就懞圈了：人眼和圖像並不在一個坐標系中，甚至和場景的物體都不在同一個坐標系中。那直接用eye_pos和圖像坐標$(u,v)$顯然無法得到正確的camera ray。

那不在同個坐標系，那可以根據之前學的MVP變換（第七章内容）將圖像坐標系變換到世界坐標系中不就行了。但是回顧整個變換過程，我們還需要知道znear和zfar平面位置，但是題目中并未給出，這下徹底懵了。最后查找到相關材料Scratchapixel-Generating Camera Rays。下面就總結下camera rays到底是怎麽生成的，分析下自己的思路到底哪裏出了問題導致無法解題的。

Generating Camera Rays

上面提到，camera ray是從相機出發，沿著相機與某個像素中心連綫方向的光綫。如下圖。

我們先簡單回顧下針孔相機模型。在相機坐標系下（假設世界坐標系和相機坐標系重合），默認相機位置在$(0,0,0)$処，構建相機坐標系$XYZ$，如下圖所示。針孔模型可以將成像平面移到物體同一側（即相機前方），距離爲$1$個單位。

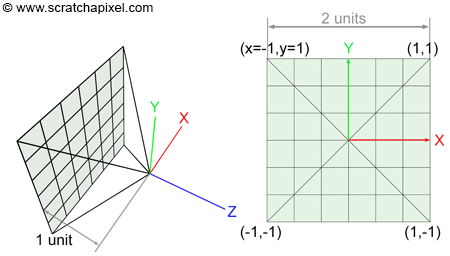
我們規定成像平面的尺寸為$[-1,1]^2$，稱爲Screen space，換而言之，就是所有的像都被壓縮在$[-1,1]^2$這個範圍的平面内。最後通過尺寸變換，將$[-1,1]^2$平面變換到$[0,w] \times [0,h]$的Raster space(渲染空間,即圖像空間）中。這個過程大致就是針孔相機模型的成像過程。

但是，生成camera ray是一個逆向過程，因爲我們已知的是Raster space中的像素坐標。這個逆向過程我們其實只需要從渲染空間變換到Screen space中就行了，因爲根據假設Screen space已經和相機空間同處於相同的世界坐標系下。如果去掉前面的假設，那麽也只需要將兩者變換到相同世界坐標系中即可。

在逆向變換過程中，一步到位顯然不直觀，因此我們在中間新增一個NDC space(Normalized Device Coordinates)，如下圖所示。這個NDC space就是Raster space標準化到$[0,1]^2$平面的結果。

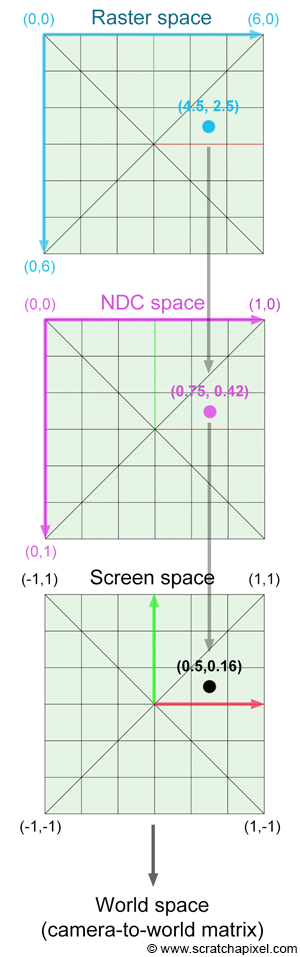
好了，整個流程大致就是上面說的這樣，那接下來就是具體推導了。

假設Raster space中像素位置為$(Pixel_x, Pixel_y)$，NDC space中坐標爲$(PixelNDC_x, PixelNDC_y)$，Screen space中坐標為$(PixelScreen_x, PixelScreen_y)$， 那麽：

$$ \begin{align} PixelNDC_x &= \frac{(Pixel_x + 0.5)}{ImageWidth} \\[2ex] PixelNDC_y &= \frac{(Pixel_y + 0.5)}{ImageHeight}\\[2ex] PixelScreen_x &= 2 * PixelNDC_x - 1 \\[2ex] PixelScreen_y &= 1- 2* PixelNDC_y \end{align} $$

這裏$PixelScreen_y$的符號發生變化，是因爲從NDC space到Screen space時，坐標軸發生翻轉。

至此還未結束，因爲圖像的寬高比并非$1:1$，而變換到Screen space后明顯圖像被壓縮了，因此我們要在Screen space中，將其比例復原，這樣才能保證camera ray的方向是正確的。如下圖。

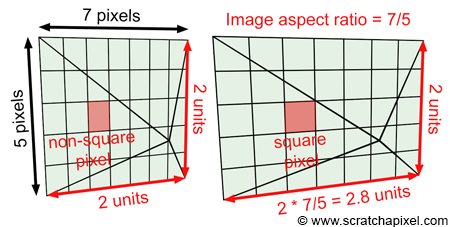
$$ \begin{align} ImageAspectRatio &= \frac{ImageWidth}{ImageHeight} \\[2ex] PixelCamera_x &= (2 * PixelNDC_x - 1) * ImageAspectRatio \\[2ex] PixelCamera_y &= (1 - 2*PixelNDC_y) \end{align} $$

注意，這裏$PixelCamera_x$和$PixelCamera_y$和原文中的不同，但是個人推導后覺得是原文中的符號取錯了。

最後，我們還需要考慮視場角$\alpha$的影響。之前我們默認設置了成像平面位於相機前方單位$1$的位置，且成像平面尺寸為$[-1,1]^2$，那麽此時視場角為$90^{\circ}$。而視場角對於不同光學模組是不同的，爲了在不同視場角下依然能看到整個畫面，因此還要將Screen space中的尺寸根據視場角進行縮放。

$$ \begin{align} PixelCamera_x &= (2 * PixelNDC_x - 1) * ImageAspectRatio * tan(\frac{\alpha}{2})\\[2ex] PixelCamera_y &= (1 - 2*PixelNDC_y) * tan(\frac{\alpha}{2}) \end{align} $$

至此，作業5生成camera ray部分就能完成了。下面是參考代碼。

1
2
3
4
5
6

float imageAspectRatio = imageWidth / (float)imageHeight; 
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio; 
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180); 
Vec3f rayOrigin(0); 
Vec3f rayDirection = Vec3f(Px, Py, -1) - rayOrigin;
rayDirection = normalize(rayDirection); // it's a direction so don't forget to normalize

One more thing

上面我們假設了相機坐標系與世界坐標系重合，且相機位於$(0,0,0)$処。但是，實際中，我們希望相機是在世界坐標系的任意位置。那麽爲了保證相機、成像平面、場景物體都處於同一個坐標系中，我們就需要繼續將相機和成像平面從相機坐標系中變換到世界坐標系。如下圖。

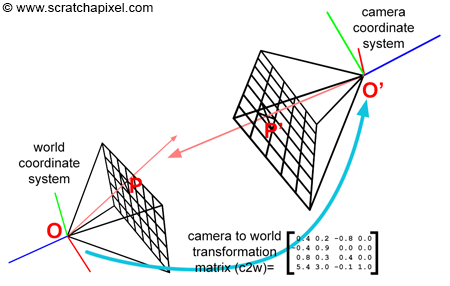
這部分就是《Games101》課程中MVP變換中Model transform的逆變換，具體參考課程課件或《Fundamentals of Computer Graphics》。下面給出加入這部分變換的代碼片段。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

float imageAspectRatio = imageWidth / imageHeight; 
float Px = (2 * ((x + 0.5) / imageWidth) - 1) * tan(fov / 2 * M_PI / 180) * imageAspectRatio; 
float Py = (1 - 2 * ((y + 0.5) / imageHeight) * tan(fov / 2 * M_PI / 180); 
Vec3f rayOrigin = Point3(0, 0, 0); 
Matrix44f cameraToWorld; 
cameraToWorld.set(...); // set matrix 
Vec3f rayOriginWorld, rayPWorld; 
cameraToWorld.multVectMatrix(rayOrigin, rayOriginWorld); 
cameraToWorld.multVectMatrix(Vec3f(Px, Py, -1), rayPWorld); 
Vec3f rayDirection = rayPWorld - rayOriginWorld; 
rayDirection.normalize(); // it's a direction so don't forget to normalize

總結

對比自己解題思路和標準解法，主要錯誤在於坐標系選擇錯誤以及在變換到Screen space的$[-1,1]^2$尺寸后沒有考慮圖像壓縮導致位置不正確的問題，也就將視場角和圖像寬高比的使用理解錯誤。綜上，實踐是檢驗真理的唯一標準。如果不是作業5，根本不知道自己模型變換其實掌握的並不好！！！！