現實中，許多物體表面接受到的光不僅僅來自光源，還來自其他反射表面。這通常被稱爲間接光照或相互光照。根據這一性質可知，任意一個表面都可能被場景中所有其他表面照亮，這就導致計算複雜度為$\mathcal{O}(N^2)$，因此這一問題的處理也被稱爲“全局光照問題”。本章節就將介紹兩種處理方式：Particle Tracing和Path Tracing，最後將討論直接光照。

先來看看下圖的場景，左側為間接光照，中間為直接光照，右側為現實中觀察到的結果，它是由左側和中間結合得到的。這三幅圖都是渲染得到的。

Particle Tracing for Lambertian Scenes

一切都從第十八章介紹的傳輸方程開始。

$$ L_s(\mathbf{k}_o) = \int_{all\ \mathbf{k}_i}\rho(\mathbf{k}_i, \mathbf{k}_o)L_f(\mathbf{k}_i)\cos{\theta_i}\mathrm{d}\sigma_i $$

其物理模型如下圖所示。

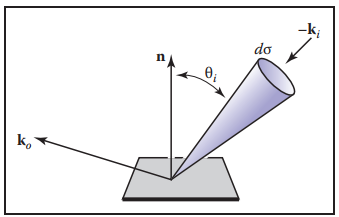
儅為Lambertian場景時，傳輸方程退化為： $$ L_s = \frac{R}{\pi}\int_{all\ \mathbf{k}_i}L_f(\mathbf{k}_i)\cos{\theta_i}\mathrm{d}\sigma_i $$

其中，$R$為漫反射係數。利用有限元分析法，將場景看成由$N$個表面構成，每個表面的irradiance$L_i$為： $$ L_i = E_i + \frac{R_i}{\pi}\sum_{j=1}^{N}k_{ij}L_j $$

其中，$E_i$為表面自身的發射輻射率（發光體），$R_i$為反射率，$k_{ij}$是原始積分表示相關的常數。求解這個綫性方程組，就能渲染出$N$個固定顔色多邊形。這種方法稱爲radiosity(輻射度法)。

對於radiosity的另一種方法是利用統計模擬，通過隨機追蹤場景中從光源出發的“粒子”，這就是粒子追蹤的一種形式。首先，先回顧面積為$A$的Lambertian表面的輻射照度irradiance$L$定義。 $$ L = \frac{\Phi}{\pi A}\tag{23.1} $$

其中，$\Phi$表示表面發射出的能量，這裏不區分是光譜能量還是RBG能量。如果表面發射能量為$\Phi_e$，入射能量為$\Phi_i$以及反射率$R$，則等式(23.1)可寫爲 $$ L = \frac{\Phi_e + R\Phi_i}{\pi A} $$

這樣，我們只需要知道每個三角形網格的$\Phi_e$和反射率$R$，就能迭代處理照明。下面詳細説説粒子追蹤的各部分細節。

現假設每個三角形網格中每個紋理像素初始irradiance為： $$ L = \frac{\Phi_e}{\pi A} $$

如果一個給定三角形網格面積為$A$，其有$n_t$個紋理像素，并且每個粒子携帶能量為$\phi$，那麽每個三角形網格的irradiance增量為： $$ \Delta L = \frac{n_t\phi}{\pi A} $$

這樣，只要追蹤的粒子與表面發生碰撞，則該位置能量就需要增加，然後再以一定概率判斷是否要讓該粒子發生反射，如果發生反射，則選擇一個方向並調整其能量。反射概率$p$通常會設爲$p = R$。

先説説能量調整方式，通常粒子在傳播過程中既不增加能量也不減少能量，直到它與表面發生作用被吸收，最終消散在環境中。那麽粒子在表面發生反射的能量可以調整爲： $$ \phi’ = \frac{R\phi}{p}\tag{23.2} $$

根據上式(23.2)，需要討論$p$與$R$的關係，儅$p>R$時，能量減少；儅$p<R$時，能量增加。這裏能量增加并不影響能量守恆，因爲$p<1$，反射的發生是服從概率$p$的，所以，總會有一點不發生反射，那麽此時粒子能量就被完全吸收了。可以參考下圖過程理解，假設圖中的反射概率為$p = 0.5$。

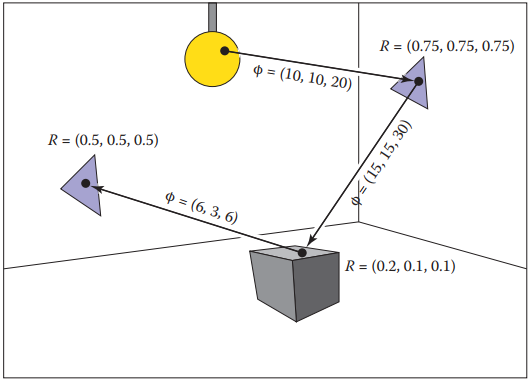
接著説説反射方向怎麽生成。在第十四章中，通過兩個均匀分佈的隨機變量$(\xi_1, \xi_2)$可以生成服從Lambertian分佈的向量： $$ \mathbf{a} = \left(\cos{(2\pi\xi_1)}\sqrt{\xi_2}, \sin{(2\pi\xi_1)}\sqrt{\xi_2}, \sqrt{1-\xi_2}\right) \tag{23.3} $$

假設要在某個三角形網格中生成隨機方向向量，那麽最直觀的方式是在該三角形網格上構建坐標系，然後在該坐標系中定義新的方向向量，而某個平面的正交坐標系構建在第七章中也已提到過。

$$ \begin{array}{l} \mathbf{w} = \frac{\mathbf{n}}{||\mathbf{n}||},\\[2ex] \mathbf{u} = \frac{\mathbf{p}_1 - \mathbf{p}_0}{||\mathbf{p}_1 - \mathbf{p}_0||}, \\[2ex] \mathbf{v} = \mathbf{w} \times \mathbf{u} \end{array} $$

其中，$\mathbf{n}$為三角形網格已知法向量，$\mathbf{p}_i$為三角形網格的頂點。這樣，結合公式(23.3)可得新的方向向量為： $$ \mathbf{a} = \cos{(2\pi\xi_1)}\sqrt{\xi_2}\mathbf{u} + \sin{(2\pi\xi_1)}\sqrt{\xi_2}\mathbf{v} + \sqrt{1-\xi_2}\mathbf{w} \tag{23.4} $$

至此，我們就可以得到一個完整的粒子追蹤過程，其僞代碼實現如下（令$p= 0.5$）。

粒子追蹤的方法對於漫反射場景的預計算是非常友好的，但是對於一般性的BRDF場景或者包含許多物體的場景是有問題的。

Path Tracing

路徑追蹤path tracing，它是從觀察位置“發出”光綫，追蹤其到光源的路徑。通常路徑追蹤用於計算間接光照。這一節將介紹路徑追蹤的“暴力”解法，下一節會介紹一些高效的解法，並加入直接光照。下面開始吧！！！

同樣先回顧完整的傳輸方程：

$$ L_s(\mathbf{k}_o) = L_e(\mathbf{k}_o) + \int_{all \ \mathbf{k}_i}\rho(\mathbf{k}_i, \mathbf{k}_o)L_f(\mathbf{k}_i)\cos{\theta_i}\mathrm{d}\sigma_i $$

對其使用蒙特卡洛積分，令采樣數$N=1$，則傳輸方程可以近似表示為 $$ L_s(\mathbf{k}_o) \approx L_e(\mathbf{k}_o) + \frac{\rho(\mathbf{k}_i,\mathbf{k}_o)L_f(\mathbf{k}_i)\cos{\theta_i}\mathrm{d}\sigma_i}{p(\mathbf{k}_i)}\tag{23.5} $$

這樣，就將問題轉換爲，根據概率密度函數$p$選擇一個隨機方向$\mathbf{k}_i$。這裏$L_f(\mathbf{k}_i)$也是未知的，但是根據傳輸方程的含義，可以采用遞歸的方式進行，即尋找$\mathbf{k}_i$方向上的光綫擊中的表面，直到光源爲止。如下圖所示。這種方法假設了最終光源出是不發生反射的，并且在到達光源前可以持續遞歸。

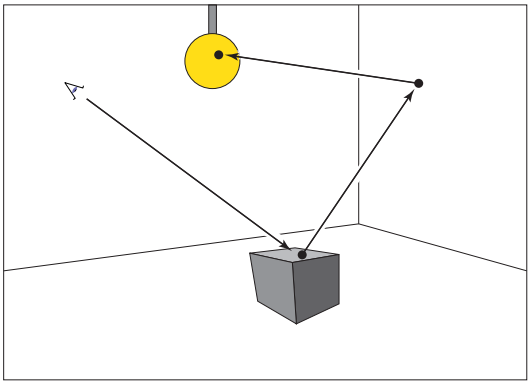
下面先説説蒙特卡洛積分中，概率密度函數$p(\mathbf{k}_i)$的選擇。因爲我們考慮的是Lambertian模型，那麽其BRDF為$\rho = \frac{R}{\pi}$，這樣我們定義采樣概率密度函數為： $$ p(\mathbf{k}_i) = \frac{\cos{\theta_i}}{\pi} $$

這樣，將概率密度函數帶入等式(23.5)可得： $$ L_s(\mathbf{k}_o) \approx L_e(\mathbf{k}_o) + RL_f(\mathbf{k}_i) $$

對於隨機方向的選擇，可以參考公式(23.4)給出。

僞代碼如下：

這種方式生成的圖片噪聲非常多，一個原因是因爲采樣數量少($N = 1$)，另一個和光源尺寸相關。由於任意一條采樣光綫可能都不會“擊中”光源，這樣其對最終的貢獻為零，那麽爲了保證最終表面顔色接近$1$，則光源的顔色必須遠大於$1$。

Accurate Direct Lighting

直接光照影響的是陰影的表現，本節結合第四章和第十章内容進行精確化直接光照介紹，比第十章内容更物理化，其核心思想依然是第四章中向光源發出shadow rays進行判斷，但本節結合傳輸方程進行。

對於傳輸方程，或説渲染方程，其有兩種形式，一種是基於立體角的積分，一種是基於位置的積分[2]。下面就以基於位置的傳輸方程進行説明。

Mathematical Framework

計算光源對一個不發光表面的直接光照，根據第十八章第二節的内容，其傳輸方程為：

$$ L_s(\mathbf{x}, \mathbf{k}_o) = \int_{all\ \mathbf{X}'}\frac{\rho(\mathbf{k}_i, \mathbf{k}_o)L_e(\mathbf{x}',-\mathbf{k}_i)v(\mathbf{x}, \mathbf{x}')\cos\theta_i\cos\theta'}{||\mathbf{x} - \mathbf{x}'||^2} \mathrm{d}A'\tag{23.6} $$

其中， $L_e$為源的出射輻射率，$v(\mathbf{x}, \mathbf{x}’)$為可見函數。

$$ v(\mathbf{x}, \mathbf{x}') = \begin{cases} 1, &\text{if x “see" x'} \\ 0, &\text{otherwise} \end{cases} $$

等式(23.6)可用如下模型解釋。

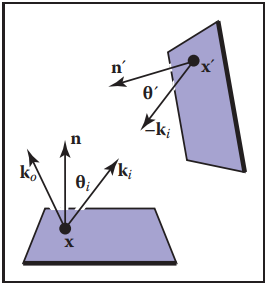
對等式(23.6)使用蒙特卡洛積分，那麽我們需要對相對光源進行服從概率密度為$p$的采樣，即獲得$\mathbf{x}’$。 $$ L_s(\mathbf{x}, \mathbf{k}_o) \approx \frac{\rho(\mathbf{k}_i, \mathbf{k}_o)L_e(\mathbf{x}’, -\mathbf{k}_i)v(\mathbf{x}, \mathbf{x}’)\cos\theta_i\cos\theta’}{p(\mathbf{x}’)||\mathbf{x}-\mathbf{x}’||^2} \tag{23.7} $$

若為均匀采樣，則可令$p = 1 / A$，其中$A$為光源面積。 $$ L_s(\mathbf{x}, \mathbf{k}_o) \approx \frac{\rho(\mathbf{k}_i, \mathbf{k}_o)L_e(\mathbf{x}’, -\mathbf{k}_i)v(\mathbf{x}, \mathbf{x}’)A\cos\theta_i\cos\theta’}{||\mathbf{x}-\mathbf{x}’||^2} \tag{23.8} $$

至此，解決了來自平面光源的直接光照。僞代碼如下：

僞代碼中未説明的幾個點。首先，需要進行餘弦截斷操作，儅$\mathbf{n} \cdot \mathbf{d}$為負數時，需要進行截斷。另外，在分母出的$||\mathbf{d}||^4$來自等式(23.8)中的兩個餘弦計算（即，$\cos\theta = \frac{n \cdot d}{||n||\times ||d||}$）和分母的距離計算。下圖為這種方式獲得的不同$N$值的軟陰影結果。

補充知識

在接下來的一節中，關於概率密度函數的設計书中并沒有展開説明，基於個人好奇心，查閲了相關論文[2]，這裏做個簡要説明，有興趣可以自己翻看論文第2.3節至第3.1節閒的内容。如有錯誤歡迎指正。

傳輸方程的積分形式可以抽象成下面的形式。 $$ L = \int_{\varphi}f_1(\psi)f_2(\psi)\cdots f_i(\psi)\mathrm{d}\mu(\psi) \tag{23.9} $$

其中，$f_i$都是嚴格非負的函數，并且這些函數在形狀或執行效率上都有很大不同。首先將這些函數$f_i$劃分成下面三類：

  • low variation (LO) ： $f_i$是先驗的，且在定義域内具有較低的方差；
  • high variation (HI) ：$f_i$是先驗的，且在定義域内具有較高的方差；
  • unknown (UN) ：$f_i$只能通過采樣得到。

這樣，將等式(23.9)進行組合，可以獲得下面形式，其中每一項都不是必須的： $$ L = \int_{\varphi}f_{LO}(\psi)f_{HI}(\psi)f_{UN}(\psi)\mathrm{d}\mu(\psi)\tag{23.10} $$

對於我們的傳輸方程而言，$f_{UN}$項是一定存在的，那麽現在就討論它與其他兩項組合時，對於最終概率密度函數選擇的影響。

  • $f_{HI}\cdot f_{UN}$組合：我們希望概率密度函數$\mathscr{G}(\psi) \propto f_{HI}(\psi)f_{UN}(\psi)$，但這個做法不適合實際應用，因爲$f_{UN}$是通過評估多個位置后近似得到，評估本身代價就高，再加上$f_{UN}$本身可能很複雜。退而求其次的辦法是令密度函數$\mathscr{G}(\psi) \propto f_{HI}(\psi)$。
  • $f_{LO}\cdot f_{UN}$組合：依照$f_{HI} \cdot f_{UN}$組合的結論，可以令密度函數為$\mathscr{G}(\psi)\propto f_{LO}(\psi)$，但我們希望概率密度函數$\mathscr{G}$是一個常數，因爲密度函數為$\mathscr{G}(\psi)\propto f_{LO}(\psi)$帶來的改進會由於$f_{UN}$產生的大方差而抵消，而且還增加計算成本。

綜上，對於傳輸方程，概率密度函數設計爲$\mathscr{G}(\psi) \propto f_{HI}(\psi)$，如果這樣依然很困難，那麽尋找一個$f_{HI}$的近似函數$\hat{f}{HI}$，令$\mathscr{G}(\psi) \propto\hat{f}{HI}(\psi)$即可。

基於上述内容，套用到我們使用的傳輸方程(23.6)中：

$$ L_s(\mathbf{x}, \mathbf{k}_o) = \underbrace{\rho(\mathbf{k}_i, \mathbf{k}_o)L_e(\mathbf{x}',-\mathbf{k}_i)}_{LO}\ \ \underbrace{\cos\theta_i\frac{\cos\theta'}{||\mathbf{x} - \mathbf{x}'||^2}}_{HI}\ \ \underbrace{v(\mathbf{x}, \mathbf{x}')}_{UN} $$

這樣，就推出概率密度函數設計需要服從： $$ p(\mathbf{x}’) \propto \cos\theta_i\frac{\cos\theta’}{||\mathbf{x} - \mathbf{x}’||^2} $$

由於餘弦計算可用向量點乘替代，所以上式替換爲： $$ p(\mathbf{x}’) \propto (k_i \cdot \mathbf{n})\frac{(-\mathbf{k}_i \cdot \mathbf{n}’)}{||\mathbf{x} - \mathbf{x}’||^2}\tag{23.11} $$

Sampling a Spherical Luminaire

對於球體光源，假設其中心位置$\mathbf{c}$及半徑$R$，同樣可以使用等式(23.8)的方式對其進行光源采樣。但是，這樣得到的結果通常會存在很多噪聲，原因在於采樣位置可能位於光源的背面，并且$\cos\theta’$的變化非常劇烈。解決方法是采用更複雜的$p(\mathbf{x}’)$來減少噪聲。

（PS：結合論文[2]中第3.2.2節，這裏的采樣方式是在方向空間(在某個立體角範圍内)中進行均匀采樣，這會導致在球體表面的不均匀性，所以這裏采用的密度函數是非均匀的。另外公式(23.11)中，HI項在不同情況下，裏面的三項依然可以劃分為LO或HI項，所以密度函數會有變化。）

首先，我們先采用非均匀密度函數$p(\mathbf{x}’)$，其正比於$\cos\theta’$。由於可以證明$p(\mathbf{x}’) \propto \frac{\cos\theta’}{||\mathbf{x}’ - \mathbf{x}||^2}$采樣複雜度相較於$p(\mathbf{x}’) \propto \cos\theta’$不變，因此這裏我們采用$p(\mathbf{x}’) \propto \frac{\cos\theta’}{||\mathbf{x}’ - \mathbf{x}||^2}$説明。

我們觀察到，利用這種方式采樣相當於在點$\mathbf{x}$処向光源方向某個立體角内對角度的均匀采樣，即密度函數$q(\mathbf{k}_i) = const$，它由觀察點$\mathbf{x}$向光源方向決定。這樣，我們需要在觀察位置$\mathbf{x}$処定義坐標系，定義方式如下。

$$ \mathbf{w} = \frac{\mathbf{c} - \mathbf{x}}{||\mathbf{c} - \mathbf{x}||} \\[2ex] \mathbf{v} = \frac{\mathbf{w} \times \mathbf{n}}{||\mathbf{w} \times \mathbf{n}||} \\[2ex] \mathbf{u} = \frac{\mathbf{w} \times \mathbf{v}}{||\mathbf{w} \times \mathbf{v}||} $$

接著定義坐標系$uvw$下方位角和極角$(\alpha, \phi)$。如下圖所示。

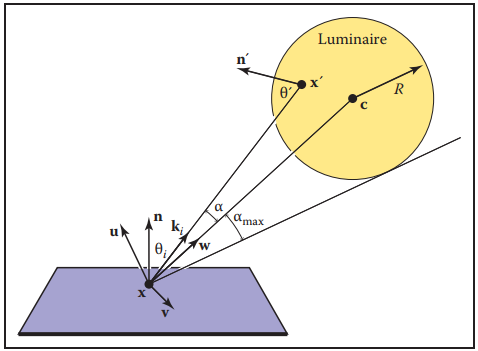
根據上圖，可知方位角$\alpha$的最大值為： $$ \alpha_{max} = \arcsin\left(\frac{R}{||\mathbf{x}-\mathbf{c}||}\right) = \arccos\sqrt{1-\left(\frac{R}{||\mathbf{x}-\mathbf{c}||}\right)^2} $$

這樣，我們就能知道某個點$\mathbf{x}$對於光源最大立體角[3]為： $$ \Omega = \int_0^{2\pi}\int_{0}^{\alpha_{max}} \sin{\theta}\mathrm{d}\theta\mathrm{d}\varphi = 2\pi(1 - \alpha_{max}) $$

那麽，$q(\mathbf{k}_i)$取值爲：

$$ q(\mathbf{k}_i) = \frac{1}{2\pi(1-\cos{\alpha_{max}})} = \frac{1}{2\pi\left(1 - \sqrt{1 - \left(\frac{R}{||\mathbf{x} - \mathbf{c}||}\right)^2}\right)} $$

那麽根據立體角與方位角與極角的關係，以及第十四章中提到的反函數采樣方式[4][5]可知:

$$ \begin{bmatrix}\cos\alpha \\[2ex] \phi\end{bmatrix} = \begin{bmatrix}1 - \xi_1 + \xi_1\cos\alpha_{max}\\ 2\pi\xi_2\end{bmatrix} \tag{23.12} $$

這樣，我們就能隨機獲得一條從點$\mathbf{x}$到光源的光綫$\mathbf{k}_i$，然後通過$(\mathbf{x} + t\mathbf{k}_i)$判斷交點位置，進行後續操作。這裏還需將$\mathbf{k}_i$用坐標表示：

$$ \mathbf{k}_i = \begin{bmatrix} u_x & v_x & w_x\\ u_y & v_y & w_y \\ u_z & v_z & w_z \\ \end{bmatrix} = \begin{bmatrix} \cos\phi\sin\alpha\\ \sin\phi\sin\alpha\\ \cos\alpha \end{bmatrix} $$

還沒有結束，我們的目的是獲得密度函數$p(\mathbf{x}’)$，這個密度函數本質是關於面積的測度。因此根據立體角與對應面積的關係，以及最開始提到$p(\mathbf{x}’)$需服從的條件可知：

$$ \mathrm{d}\Omega = \mathrm{d}A(\mathbf{x}')\frac{\cos\theta'}{||\mathbf{x}' -\mathbf{x}||^2}\\[2ex] \Rightarrow q(\mathbf{k}_i) = \frac{p(\mathbf{x}')\cos\theta'}{||\mathbf{x}' -\mathbf{x}||^2} \tag{23.13} $$

這樣，密度函數$p(\mathbf{x}’)$可得： $$ p(\mathbf{x}’) = \frac{\cos\theta’}{2\pi||\mathbf{x}’ -\mathbf{x}||^2\left(1 - \sqrt{1-\left(\frac{R}{||\mathbf{x} - \mathbf{c}||}\right)^2}\right)}\tag{23.14} $$

總結下，對於球體光源直接光照的采樣有兩個任務，一個是設計可以用於蒙特卡洛積分的概率密度函數，由等式(23.14)給出；二是獲得采樣方向或是光源上采樣位置，由等式(23.12)給出。

Nondiffuse Luminaries

對於光源來説，我們不可能限制其亮度不能隨著角度或位置的變化而變化。這樣我們就需要對前幾節中的$L_e(\mathbf{x}’)$項進行修改： $$ L_e(\mathbf{x}’) \Rightarrow L_e(\mathbf{x}’, -\mathbf{k}_i) $$

而隨方向變化的最簡單形式就是Phone-like有關法向量$\mathbf{n}’$的模式，因此可以改寫爲： $$ L_e(\mathbf{x}’, -\mathbf{k}_i) = \frac{(n+1)E(\mathbf{x}’)}{2\pi}\cos^{(n-1)}\theta' $$

其中，$E(\mathbf{x}’)$表示在點$\mathbf{x}’$処的出射輻射率，儅光源在面積上分佈不均時，$E$將不再是常數；$n$表示Phong指數，但其等於$1$時，就爲漫反射光源。

參考資料

[1] Márk, Rázsó István. “Particle tracing methods in photorealistic image synthesis.” CECSG 98 (1998): 105-117.

[2] P. Shirley, C. Wang, and K. Zimmerman, “Monte Carlo techniques for direct lighting calculations,” ACM Trans. Graph., vol. 15, no. 1, pp. 1–36, Jan. 1996, doi: 10.1145/226150.226151.

[3] Solid angle

[4] 均匀采样问题总结

[5] 圖形學系列 Ch14-Sampling-閲讀筆記