從3D空間到2D空間中的映射稱爲viewing transformation。本章將學習如何利用矩陣運算，將已知的3D空間物體映射（可能是平行投影，也可能是透視投影）到2D空間（像平面）中。

7.1 Viewing Transformations

viewing transformations是一系列操作的總稱，這些操作主要完成從3D空間的位置（笛卡爾坐標系下的$(x,y,z)$）到圖像坐標（$(u,v)$）的變換。這一系列操作通常可分爲三個變換：

  1. camera transformation或eye transformation：用於調整相機位置和位姿；
  2. projection transformation：根據投影類型，將物體從相機空間中映射到$x \in [-1,1]$和$y \in [-1,1]$的區間中，這個區間圖像稱爲unit image。
  3. viewport transformation或windowing transformation：將unit image變換成所需的圖像尺寸。

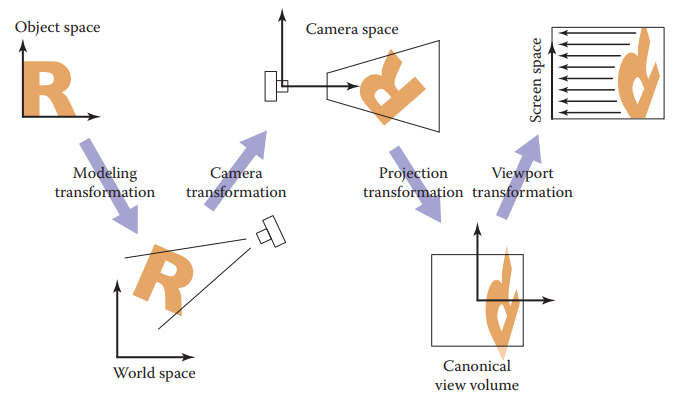
camera transformation將點的空間坐標轉換到相機坐標系下，也稱爲相機空間；projection transformation將點從相機空間中變換到標準視圖躰中，也就是$(x,y,z) \in [-1,1]^3$的立方體中；viewport transformation將標準視圖躰變換到屏幕空間，也就是最後成像。

7.1.1 The Viewport Transformation

假設所有希望看到的物體都在標準視圖躰($(x,y,z) \in [-1,1]^3$)内，相機觀察方向為$-z$，正交于標準視圖躰。縣規定$x = -1$對應圖像左邊界，$x = +1$對應圖像右邊界，$y = -1$對應圖像下邊界，$y = +1$對應圖像上邊界。假設圖像寬高為$n_x$和$n_y$，viewport transformation就是將平面$[-1,1]^2$變換到矩形$[-0.5, n_x - 0.5] \times [-0.5, n_y - 0.5]$中。

這裏忽略了$z$軸坐標的原因是，點在空間中的投影距離，并不影響它在像平面中的位置。所以可得到viewport matrix。

$$ \mathbf{M}_{vp} = \begin{bmatrix} \frac{n_x}{2} & 0 & 0 & \frac{n_x - 1}{2}\\ 0 & \frac{n_y}{2} & 0 & \frac{n_y - 1}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{7.2} $$

7.1.2 The Orthographic Projection Transformation

通常我們并不只希望獲取標準視圖體内的幾何體，而希望在觀察方向和角度固定（沿$-z$且$+y$正立）情況下，能獲得任意矩形體内的幾何體。我們在viewport matrix右側再乘上一個矩陣來獲得所希望的結果，而不是去修改viewport matrix。

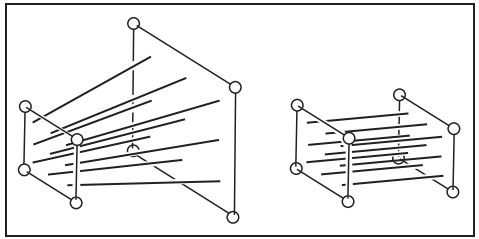
先定義任意矩形體為$[l,r] \times [b,t] \times [f,n]$，如下圖所示：

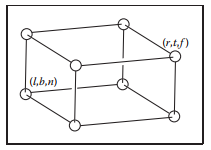
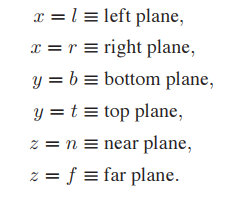
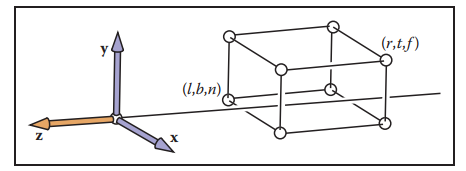
通常稱這樣的矩形骵為``orthographic view volume``，其中：

注意，通常觀察方向都是沿著$-z$方向，正立方向都是沿著$+y$軸，對於近平面$n$的值就始終大於遠平面$f$的值，即$n > f$。如下圖所示：

現在只要將orthographic view volume變換到canonical view volume，之後在利用viewport matrix變換即可。

$$ \mathbf{M}_{orth} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\ 0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\ 0 & 0 & -\frac{2}{n-f} & -\frac{n+f}{n-f}\\ 0 & 0 & 0 & 1 \end{bmatrix} \tag{7.3} $$

繪製orthographic view volume的3D綫段時，就可以結合矩陣(7.2)和矩陣(7.3)來獲取兩個端點在圖像中的位置坐標。

$$ \begin{bmatrix} x_{pixel}\\ y_{pixel}\\ z_{canonical}\\ 1 \end{bmatrix} = (M_{vp}M_{orth})\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} $$

算法框架如下：

7.1.3 The Camera Transformation

在3D空間中，我們視點位置和觀察角度通常都是任意的，因此，常用以下三個量來定義視點：

  1. “眼睛”的位置$\mathbf{e}$；
  2. 視綫方向$\mathbf{g}$;
  3. 正立方向$\mathbf{t}$

如下圖所示

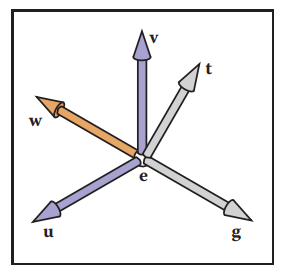
有了這三個信息，就能夠在視點位置構造一個坐標系$\mathbf{uvw}$，也是用於描述相機空間的坐標系。

$$ \begin{align} \mathbf{w} &= -\frac{\mathbf{g}}{||\mathbf{g}||}\\[2ex] \mathbf{u} &= \frac{\mathbf{t}\times\mathbf{w}}{||\mathbf{t}\times\mathbf{w}||}\\[2ex] \mathbf{v} &= \mathbf{w} \times \mathbf{u} \end{align} $$

被觀察物體改用坐標系$\mathbf{uvw}$表示，這樣，只需要變換視點位置$\mathbf{e}$和基坐標$\mathbf{uvw}$，就能將視點和被觀察物體從世界坐標系$\mathbf{o_{xyz}}$變換到相機坐標系$\mathbf{e_{uvw}}$中。

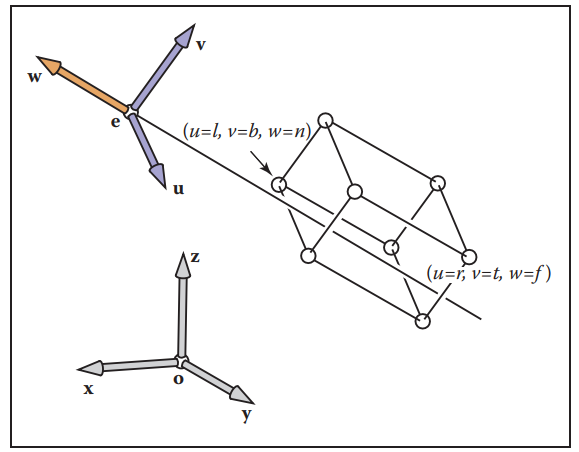
坐標系閒的變換在第六章中做了詳細説明，這裏就不多説，直接上公式：

$$ \mathbf{M}_{cam} = \begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{w} & \mathbf{e}\\ 0 & 0 & 0 & 1 \end{bmatrix}^{-1} = \begin{bmatrix} x_u & y_u & z_u & 0 \\ x_v & y_v & z_v & 0 \\ x_w & y_w & z_w & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} $$

結合前面的變換，整個viewing transformation的框架如下所示：

總結下，整個viewing transformation過程可以想像成拍照過程，先選好鏡頭和設置相片尺寸（viewport transformation）；擺放好相機和被拍攝物體（camera transformation）；按下快門（projection transformation）。

7.2 Projective Transformation

射影變換是在相機空間中進行的，通過camera transformation后，視點位置位於相機空間的原點，觀察方向沿著$-z$軸。

在透視投影中，物體在像平面的尺寸，與物體離視點距離的倒數($1/z$)成正比。如下圖：

figure7.8

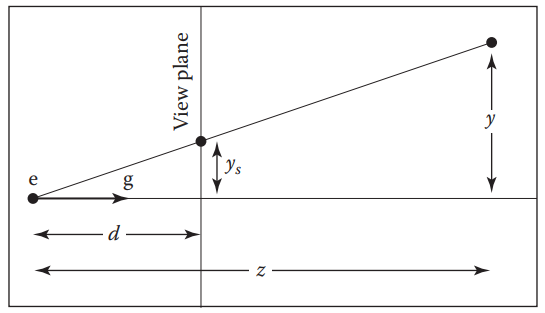
圖中，$d$表示視平面離視點的距離，$y_s$表示物體在視平面上$y$軸上的成像位置。利用相似三角形，很容易得到： $$ y_s = \frac{d}{z}y $$

一般的仿射變換為： $$ x’ = ax + by + cz + d $$

這裏約束齊次坐標系最後一維$w = 1$；若取消這個約束，那麽可以擴展出更多變換，變換形式變化成如下形式： $$ x’ = \frac{ax+by+cz+d}{ex+fy+gz+h} $$

這樣就可獲得關於$x$、$y$和$z$的三個變換函數：

$$ \begin{align} x' &= \frac{a_1x + b_1y + c_1z + d_1}{ex+fy+gz+h}\\[2ex] y' &= \frac{a_2x + b_2y + c_2z + d_2}{ex+fy+gz+h}\\[2ex] z' &= \frac{a_3x + b_3y + c_3z + d_3}{ex+fy+gz+h} \end{align} $$

這三個變換函數的唯一約束就是分母是相同的。同樣也可使用矩陣形式表示：

$$ \begin{bmatrix} \tilde{x}\\ \tilde{y}\\ \tilde{z}\\ \tilde{w} \end{bmatrix} = \begin{bmatrix} a_1 & b_1 & c_1 & d_1\\ a_2 & b_2 & c_2 & d_2\\ a_3 & b_3 & c_3 & d_3\\ e & f & g & h \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} \\[7ex] \Rightarrow (x',y',z') = (\tilde{x}/\tilde{w}, \tilde{y}/\tilde{w},\tilde{z}/\tilde{w}) $$

可用這種形式表示的變換都可稱爲射影變換(projective transformation)或單應性。

7.3 Perspective Projection

假設，在3D空間中，視點位於原點，觀測方向沿$-z$軸，可是距離由遠近平面限制。 在透視變換中，將近平面作爲像平面，這樣可簡化推導。更簡單的理解是，先將物體透視投影到一個矩形體上，再利用正交投影進行後續操作。如下面兩圖所示：

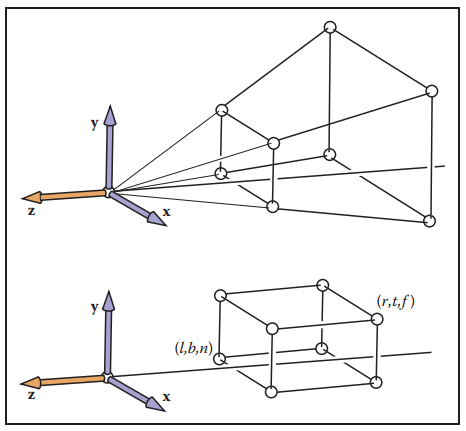
這裏先回顧圖(7.8)，將圖中$y_s$的計算用矩陣可表示爲：

$$ \begin{bmatrix} y_s\\ 1 \end{bmatrix} \sim \begin{bmatrix} d & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} y\\ z \\ 1 \end{bmatrix} $$

類似的，在3D空間中，$x$和$y$均可按上面的方式處理，得到變換矩陣：

$$ \mathbf{P} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{bmatrix} $$

這個矩陣中的第1、2、4行已實現了透視方程，而第3行是與$z$坐標有關，這行的計算值會在之後物體遮擋部分使用到（z-buffer算法）。那第3行的參數是什麽呢？這裏可做如下假設來獲取第3行的參數：

  1. 齊次坐標係中，坐標$(x,y,z,1)$和$(kx,ky,kz,k)$是表示同一個點；
  2. 位於近平面上的點，經過投影后仍在近平面上；
  3. 位於遠平面上的點，經過投影后仍在遠平面上；

根據這以上的假設，可知：

$$ \mathbf{P}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ ?\\ z \end{bmatrix} \tag{1} $$

對於近平面上的點變換前後始終是：

$$ \begin{bmatrix} x\\ y\\ n\\ 1 \end{bmatrix} \Rightarrow \begin{bmatrix} x\\ y\\ n\\ 1 \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ n^2\\ n \end{bmatrix} $$

與公式(1)對比可知，第3行的計算方式如下：

$$ \begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} x\\ y\\ n\\ 1 \end{bmatrix} = n^2 \\[4ex] \Rightarrow An + B = n^2 \tag{2} $$

同理，對於遠平面可得： $$ Af + B = f^2 \tag{3} $$

聯立等式(2)、(3)，求解方程組可得：

$$ \begin{cases} An+B = n^2\\ Af+B = f^2 \end{cases} \Rightarrow \begin{cases} A = n+f\\ B = -nf \end{cases} $$

這樣，就能獲得完整的透視變換矩陣：

$$ \mathbf{P} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix} $$

對於view volume中任一點進行透視變換可得：

$$ \mathbf{P}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ (n+f)z-fn\\ z \end{bmatrix} \sim \begin{bmatrix} \frac{nx}{z}\\ \frac{ny}{z}\\ n+f-\frac{nf}{z}\\ 1 \end{bmatrix} $$

而對於矩陣$\mathbf{P}$的逆變換同樣非常簡單：

$$ \mathbf{P}^{-1} = \begin{bmatrix} \frac{1}{n} & 0 & 0 & 0\\ 0 & \frac{1}{n} & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -\frac{1}{nf} & \frac{n+f}{nf} \end{bmatrix} \\[4ex] \Rightarrow \mathbf{P}^{-1} = \begin{bmatrix} f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 0 & nf\\ 0 & 0 & -1 & n+f \end{bmatrix} $$

至此，將透視變換矩陣和之前的正交投影矩陣結合，就能得到完整的透視投影矩陣：

$$ \mathbf{M}_{per} = \mathbf{M}_{orth}\mathbf{P} = \begin{bmatrix} \frac{2n}{r-l} & 0 & \frac{l+r}{l-r} & 0\\ 0 & \frac{2n}{t-b} & \frac{t+b}{b-t} & 0\\ 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{f-n}\\ 0 & 0 & 1 & 0 \end{bmatrix} $$

這樣使用透視投影變換的viewing transformation矩陣可變爲：

$$ \mathbf{M} = \mathbf{M}_{vp}\mathbf{M}_{orth}\mathbf{P}\mathbf{M}_{cam} $$

算法框架為：

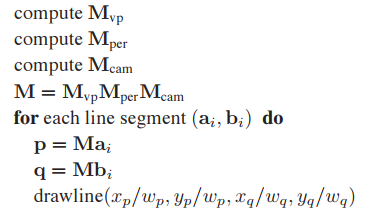
7.4 透視投影變換的一些特點

投影前後，直綫依然是直綫，平面依然是平面；以綫段爲例，假設原綫段為： $$ \mathbf{q} + t(\mathbf{Q}-\mathbf{q}) $$

經過變換矩陣$\mathbf{M}$后： $$ \mathbf{M}\mathbf{q} + t(\mathbf{M}\mathbf{Q}-\mathbf{M}\mathbf{q}) \equiv \mathbf{r} + t(\mathbf{R}-\mathbf{r}) $$

對於3D綫段可變爲：

$$ \frac{\mathbf{r} + t(\mathbf{R}-\mathbf{r})}{w_r + t(w_R - w_r)} \\[4ex] \Rightarrow \frac{\mathbf{r}}{w_r} + f(t)\left(\frac{\mathbf{R}}{w_R} - \frac{\mathbf{r}}{w_r}\right) $$

其中，$f(t) = \frac{w_Rt}{w_r + t(w_R-w_r)}$。這一系列變換過程并未改變點的順序，所以從綫段依然變換爲綫段，平面依然變換爲平面。

7.5 Field-of-View

通常，我們會使用$(l,r,b,t)$和$n$來定義可視窗口，其中：

$$ l = -r,\\ b = -t $$

如果成像尺寸(像素)為$n_x \times n_y$，那麽： $$ \frac{n_x}{n_y} = \frac{r}{t} $$

這個比例可稱爲aspect ratio。如果按下圖中所示，在定義$\theta$角度，就能夠簡化可視窗口模型。

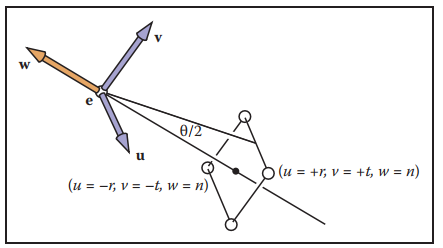
其中： $$ \tan{\frac{\theta}{2}} = \frac{t}{|n|} \tag{4} $$

該$\theta$就稱爲field-of-view，等式(4)中定義了垂直方向的field-of-view，同理也可定義水平方向field-of-view。這樣就能將可視窗口模型簡化爲$(n, \theta_x, \theta_y, ratio_{aspect})$即可。

FQA

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。