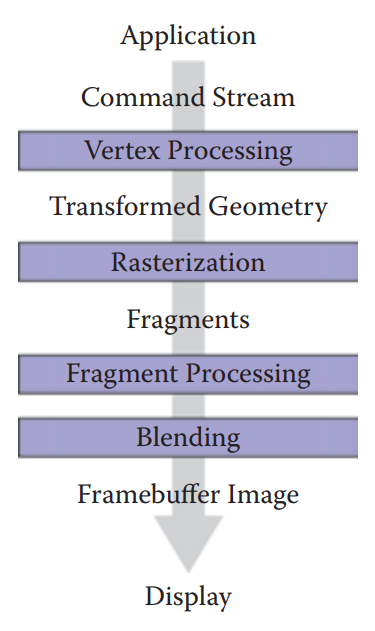
本章节介绍第二种（第一种是第四章中的ray tracing）渲染方式：逐个将物体绘制到屏幕上。两者的不同在于：ray tracing是每个像素会被哪些几何图元影响，而本章节中的渲染方式是每个几何图元影响哪些像素。这种处理几何图元占据图像像素的过程称为光栅化，这种对物体逐个光栅化的过程称为光柵化渲染。這種起始於物體，終止于圖像像素更新的流程稱爲圖形化管綫(graphic pipeline)。本章先從光柵化開始，在介紹其前後的流程分別如何進行的。Graphic pipeline整個過程如下圖所示。

8.1 Rasterization

Rasterization是整個Graphic pipeline的核心操作，之所以是核心，是因爲它將幾何圖元的數學表示轉換爲像素表示（這是個人理解）。Rasterizer需要完成兩個任務：一個是枚舉出覆蓋輸入圖元的所有像素；另一個就是對圖元的屬性進行插值。

8.1.1 繪製直綫

隱式直綫方程表示

假设直线上有两点$(x_0, y_0)$和$(x_1, y_1)$，该直线的隐式表达如下： $$ f(x, y) \equiv (y_0 - y_1)*x + (x_1 - x_0) * y + x_0y_1 - x_1y_0 = 0 \tag{8.1} $$

这里假设$x_0 \leq x_1$，直线的斜率$m$可表示为： $$ m = \frac{y_1 - y_0}{x_1 - x_0} $$

接下去的讨论中，假设$m \in (0,1]$；此時， 若點沿著直綫運動，其在$x$軸上的變化速度要快於$y$軸上的變化速度。类似讨论可以推广到$m \in (-\infty, -1]$、$m \in (-1, 0]$和$m \in (1, \infty)$。

直綫光柵化

The midpoint algorithm的框架如下：

該算法從左至右繪製直綫，$x$和$y$均爲整數，在some condition下，$y$方向會移動一個像素。因此整個流程的關鍵就是如何定義some condition。

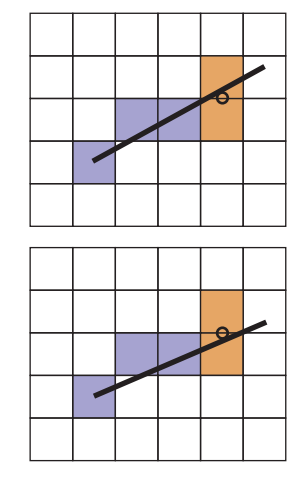
一種便捷的做法就是，觀察兩個備選像素的中點(midpoint)。假設當前綫段繪製到$(x,y)$點，那麽下一個點可能是$(x+1,y)$或$(x+1,y+1)$中的一個，那麽這兩個備選點的中點為$(x+1,y+0.5)$，如果直綫在中點下方穿過，那麽下一個繪製點就是$(x+1,y)$，否則為$(x+1,y+1)$。而判斷直綫在點上方還是下方的方式也非常簡單，就是將點帶入直綫方程(8.1)判斷符號即可。如下圖所示：

那麽算法框架即可升級爲：

$y = y_0$
for $x = x_0$ to $x_1$ do
　　draw($x,y$)
　　if ( $f(x+1, y+0.5) < 0$ ) then
　　　　$y = y + 1$

現在這個框架已經能很好的進行繪製直綫了，但是效率依舊不高。如果將判斷條件改爲增量判斷，可提高整個算法框架的執行效率。那下面來看看增量判斷是如何做的。

依舊假設直綫當前繪製點為$(x,y)$，那麽比較一下兩個等式：

$$ f(x+1,y) = f(x,y) + (y_0 - y_1)\\ f(x+1,y+1) = f(x,y) + (y_0 - y_1) + (x_1 - x_0) $$

觀察可發現，下一個繪製點的判斷都用到了當前繪製點的信息，這樣就能將算法的修改爲：

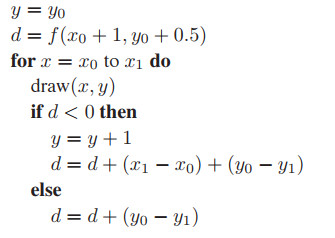
雖然增量法比非增量法高效，但是會引入數值誤差的纍積，但是綫段很少有幾千個像素的長度，因此，這種數值誤差并不致命。另外，由於$(x_1 - x_0)$和$(y_0 - y_1)$是確定的，因此可以存成變量之後反復使用，有時我們希望編輯器就能做到，但并非如此，所以在某些對效率嚴格要求的環境下，需要手動檢查編譯結果。

8.1.2 三角形光柵化

三角形的光柵化和直綫光柵化有類似的問題，但也有其特有問題，其一就是插值問題。假設平面上的三角形由點$p_0 = (x_0, y_0)$、$p_1 = (x_1, y_1)$和$p_2 = (x_2, y_2)$構成，即已知三角形三個頂點屬性，先要獲得三角形内任意一點屬性，可通過Gouraud interpolation方式獲得，例如，已知三個頂點顔色向量分別爲$\mathbf{c}_0$、$\mathbf{c}_1$和$\mathbf{c}_2$，三角形内任意一點重心坐標爲$(\alpha, \beta, \gamma)$，那麽任意點顔色可表示為： $$ \mathbf{c} = \alpha \mathbf{c}_0 + \beta \mathbf{c}_1 + \gamma \mathbf{c}_2 $$

三角形光柵化的另一個問題就是共邊和共點問題。假設有兩個不同顔色三角形有一條公共邊，爲了保證繪製后，兩三角形閒不會有空洞出現，通常會使用midpoint algorithm繪製三角形各邊並用插值填充三角形内區域，這會導致，這條共邊的顔色和三角形繪製順序有關，這顯然是不合理的。而解決這個問題的辦法也非常簡單粗暴：判斷共邊上的像素點重心是在哪個三角形内，那麽該像素就屬於對應三角形。（當然，還會存在像素點重心剛好在共邊上的問題，這在之後會提供解決方法）

結合上面兩個問題，可以把三角形光柵化歸結爲重心坐標測試問題，暴力算法如下：

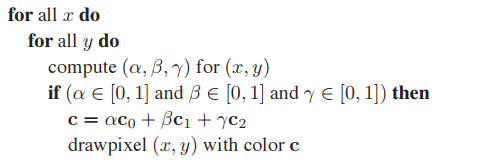
顯然，通過一些優化，能大幅提高該光柵化算法的效率。顯然，不需要對整幅圖像的像素點進行遍歷，只需遍歷覆蓋當個三角形區域即可：

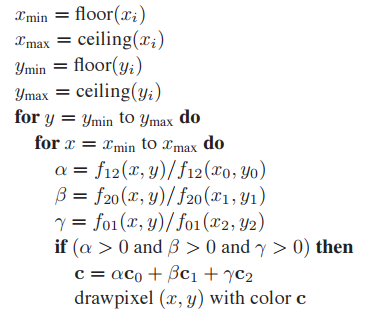
其中:

$$ \begin{align} f_{01}(x,y) &= (y_0 - y_1)x + (x_1 - x_0)y + x_0y_1 - x_1y_0\\ f_{12}(x,y) &= (y_1 - y_2)x + (x_2 - x_1)y + x_1y_2 - x_2 y_1\\ f_{20}(x,y) &= (y_2 - y_0)x + (x_0 - x_2)y + x_2y_0 - x_0y_2 \end{align} $$

算法中只測試$\alpha > 0$，而不是測試$\alpha \in (0,1)$。這是因爲儅$\alpha$、$\beta$、$\gamma$都爲正數時，它們都會小於$1$，因爲$\alpha + \beta + \gamma = 1$。

同样，该算法也能用增量式进行优化。例如，内循环中$f_{12}(x + 1,y) = f_{12}(x,y) + A$，外循环中$f_{12}(x,y+1) = f_{12}(x,y) + B$。其中$A = \frac{(y_0 - y_1)}{f_{12}(x_0, y_0)}$，$B = \frac{(x_1 - x_0)}{f_{12}(x_0, y_0)} $。其他项类似处理即可。

Dealing with Pixels on Triangle Edges

現在來解決像素點重心正好落在兩三角形共邊上的問題。最簡單的方式就是隨便挑選歸屬其中一個三角形。但還有另一種方式判斷：選取任意一屏幕外點，若該屏幕外點在共邊一側，那麽該共邊就屬於該側三角形。如下圖：

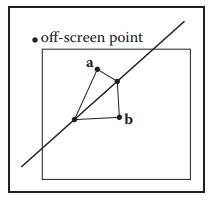
那麽屏幕外的點如何選取，因爲不管如何選取，都會存在屏幕外點落在共邊所在直綫上。所以屏幕外點可任意選取，通常使用點$(x,y) = (-1,-1)$。在光柵化算法内部不進行這種情況判斷，所以，屏幕外點是否落在共邊直綫上需在外部處理。這樣，整個算法可升級爲：

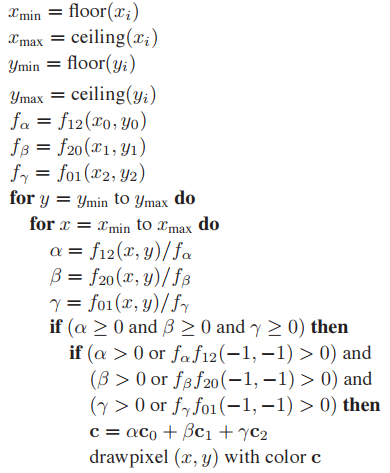
上面的伪代码依然包含许多细节需要注意，例如除零问题，浮点误差等等，还有即使两三角形共边，但是指向若相反时，符号也会相反。这些在设计光栅化程序时都需要注意。

8.1.3 Clipping

簡單的將圖元變換到像平面再光柵化往往效果不佳。這是因爲如果圖元空間位置位於可視區域外時，例如視點的後方，不加處理的光柵化就會導致錯誤的結果。回顾透视变换后的结果：

$$ \begin{bmatrix} x'\\ y'\\ z'\\ w' \end{bmatrix} = P * \begin{bmatrix} x \\ y \\ z \\ 1\\ \end{bmatrix} = \begin{bmatrix} nx\\ ny\\ (n+f)z - fn\\ z\\ \end{bmatrix} \sim \begin{bmatrix} \frac{nx}{z}\\ \frac{ny}{z}\\ n+f - \frac{fn}{z}\\ 1\\ \end{bmatrix} $$

单独观察$z’ = n+f - \frac{fn}{z}$，其图像如下：

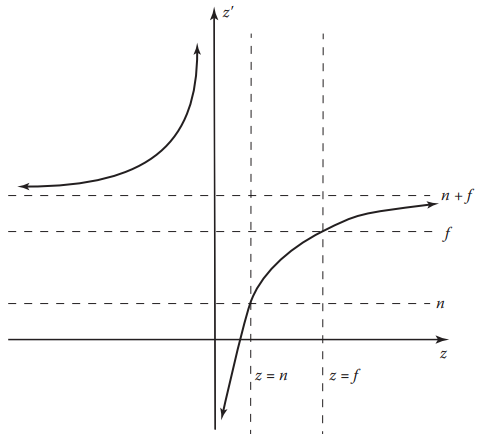
当$z < 0 $时，$z'$则变为正值，这就出现了下面情况：

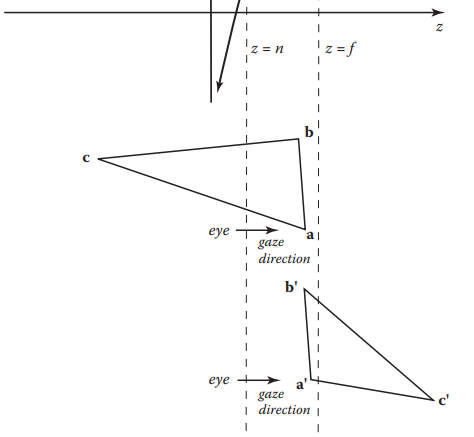
基於這個原因，光柵化前需要進行clipping操作，用於移除可視範圍外的部分。下面是個三角形被裁切的例子。

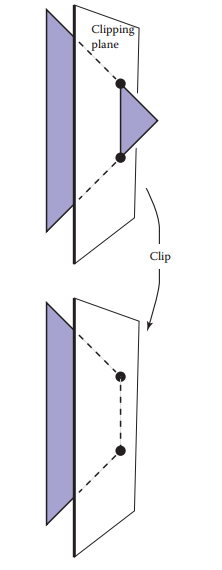
這裏有兩種常用的clipping方法：

  1. 在世界坐標系下，使用視錐體的六個面作爲clipping plane;
  2. 在4D變換空間進行齊次坐標除法前；

這兩種方法都能利用下面的算法框架有效實現：

方法1: Clipping Before the Transform

该方法实现比较直接，问题在于”六个平面如何表示？“通过視錐體的8顶点变换后，来确定平面方程。

$$ (x,y,z) = \begin{align} & (l, b, n)\\ & (r,b,n)\\ & (l,t,n)\\ & (r,t,n)\\ & (l,b,f)\\ & (r,b,f)\\ & (l,t,f)\\ & (r,t,f) \end{align} $$

這裏原書貌似有錯，書中說“利用圖5.11的逆變換作用於8個視錐體頂點”，可是圖5.11不存在

方法2: Clipping in Homogeneous Coordinate

假设在4D齐次坐标表示为$(x,y,z,w)$，那么除法前进行裁剪的平面方程如下：

$$ \begin{array}{r} -x + lw = 0,\\ x-rw = 0,\\ -y + bw = 0,\\ y-tw = 0,\\ -z + nw = 0,\\ z-fw = 0. \end{array} $$

這些平面表示同樣簡單，處理效率也比方法1來的高效。

8.1.6 Clipping against a Plane

以上兩種方法，無論選用哪個，都需要通過平面進行裁剪。這裏回顧平面方程隱函數表示： $$ f(\mathbf{p}) = \mathbf{n} \cdot (\mathbf{p} - \mathbf{q}) $$

其中，$\mathbf{p}$為平面上任意點，$\mathbf{n}$平面法向量，$\mathbf{q}$平面上某個已知點坐標。

平面隱函數也通常改寫爲: $$ f(\mathbf{p}) = \mathbf{n} \cdot \mathbf{p} + \mathcal{D} = 0 \tag{8.2} $$

有趣的是，公式(8.2)既可以表示3D中的平面，也可表示2D中的直綫，還可以表示4D中的體。所有這些實體都在其所在維度下稱爲平面。

現回到3D空間中，假設綫段$\mathbf{a}\mathbf{b}$，判斷兩個端點是否位於某個平面$f(\mathbf{p}) = 0$的兩側（假設$f(\mathbf{p}) > 0 $是在平面外側，$f(\mathbf{p})<0$是在平面内側），只需判斷$f(\mathbf{a})$和$f(\mathbf{b})$是否同號即可。若兩個端點在平面不同側，那麽，綫段$\mathbf{a}\mathbf{b}$與平面$f(\mathbf{p}) = 0$的交點可按如下方式計算：

$$ \begin{cases} \mathbf{p} = \mathbf{a} + t(\mathbf{b} - \mathbf{a}) \\ f(\mathbf{p}) = \mathbf{n} \cdot \mathbf{p} + \mathcal{D} = 0 \end{cases} \\[2ex] \Rightarrow \mathbf{n}\cdot (\mathbf{a} + t(\mathbf{b}-\mathbf{a})) + \mathcal{D} = 0 \\[2ex] \Rightarrow t = \frac{\mathbf{n}\cdot\mathbf{a} + \mathbf{D}}{\mathbf{n}\cdot(\mathbf{a}-\mathbf{b})} $$

這樣，就能快速找到被平面截斷的綫段位置。

8.2 Operations Before and After Rasterization

回顧本章節最開始的Graphic pipeline流程圖，在Rasterization之前的操作是vertex-processing，在Rasterization之後的操作是fragment processing和blending。 vertex-processing是將輸入的頂點通過modeling、viewing和projection這些變換，將其從世界坐標系變換到屏幕空間，同時計算了其他信息，例如顔色、表面法向量或紋理坐標。 fragment-processing是計算每個fragment的顔色和深度，這兩個信息可以直接使用rasterization的結果，也可使用更複雜的shading operations。 blending是將fragments按一定遮擋關係復原回圖元，最常用的做法是選擇最小深度的fragment。

8.2.1 Simple 2D Drawing

这种绘制vertex和fragment阶段基本没有进行操作，而在blending阶段，也只是颜色的简单覆盖。application层直接提供基元所有像素坐标，光栅器完成之后的所有工作。

8.2.2 A Minimal 3D pipeline

與2D繪製不同的是，進行3D繪製時，vertex-processing需要進行坐標的轉換，將圖元轉換到屏幕空間后，之後的操作與2D繪製一樣。

但是，3D繪製依然存在問題 —— 繪製順序。直覺上只需要從遠到近繪製物體就能獲得正確的結果，這就是painter's algorithm。但是其依然存在嚴重的缺陷，例如下圖的圖形使用畫家算法就無法正確繪製。

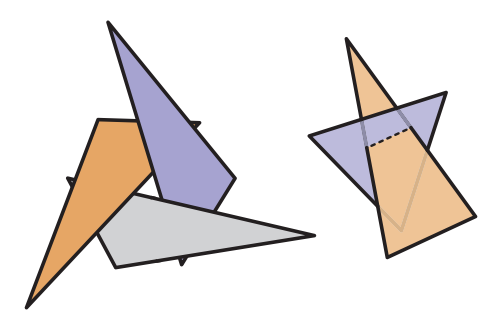
还有另外一个问题，如果“前后”顺序不存在时，畫家算法也无法有效工作。若對圖元進行深度排序后再進行繪製，這種操作有非常耗時，特別是對大型場景的渲染，這樣的排序會讓快速執行的數據流變慢。

8.2.3 Using a Z-Buffer for Hidden Surface

上面提到的畫家算法存在的缺陷是致命的，因此在實際中很少使用。取而代之的就是更簡單高效的z-buffer algorithm。該算法思路如下：對每個像素追蹤離繪製平面最近的距離，抛棄超過這個距離的位置。該距離信息存儲在每個像素點的RGB值之後，稱爲深度信息。這塊存儲深度信息的緩存通常稱爲深度緩存或z-buffer。

z-buffer算法通常是在blending階段執行，通過比較深度信息，能準確反映圖元閒的遮擋關係。由於深度緩存是最小值存儲，因此在初始化時，需要初始化為最大深度值，否則算法無法獲得正確結果。同樣，深度信息也能通過插值的方式得到。

Precision Issues

z-values通常使用非負整數表示，相比於浮點數表示，這樣占用的高速緩存最少，也就是代價最小。但同時面臨著精度問題。

假設有$\mathcal{B}$個非負整數${0,1,\cdots,\mathcal{B}-1}$，現將$z = n$的進平面映射到$0$，$z=f$的遠平面映射到$\mathcal{B}-1$，這裏暫時假設$z,n,f$均爲正數。相鄰兩個整數閒的表示精度為： $$ \Delta{z} = \frac{f-n}{\mathcal{B}} $$

只要$\Delta{z}$越小，説明表示的精度越高；在計算機中，$\mathcal{B} = 2^b$，其中$b$表示二進制位數。因此，減小$\Delta{z}$有兩種方式：第一種是讓$n$和$f$更接近；第二種是增大$b$值。由於$b$值往往都是固定的，所以只能通過第一種方式調整。

在生成透視圖像時，z-buffer的精度問題就會伴隨而來。觀察透視變換矩陣中，z值的計算如下，： $$ z = n+f - \frac{fn}{z_w} $$

可看出，$\Delta{z}$是與$z_w$存在反比關係的，也僅與$z_w$有關。再做如下推導：

$$ \begin{align} &\begin{cases} z_0 = n + f - \frac{fn}{{z_w}_0} \\[3ex] z_1 = n + f - \frac{fn}{{z_w}_1} \end{cases} \\[4ex] \Rightarrow &\Delta{z} = z_1 - z_0 = \frac{fn}{{z_w}_0} - \frac{fn}{{z_w}_1} = \frac{({z_w}_1 - {z_w}_0) fn}{{z_w}_0 {z_w}_1} \\[4ex] \Rightarrow &\Delta{z} = \lim_{{z_w}_1 \rightarrow {z_w}_0}\frac{({z_w}_1 - {z_w}_0) fn}{{z_w}_0 {z_w}_1} \approx \frac{fn\Delta{z_w}}{z_w^2} \\[4ex] \Rightarrow &\Delta{z_w} \approx \frac{z_w^2\Delta{z}}{fn} \\[4ex] \Rightarrow &\Delta{z_w^{max}} \approx \frac{f\Delta{z}}{n} \end{align} $$

從這個式子中可以看出，若按直覺（爲了不丟失視點前方的物體）將進平面$n$設爲$0$，那麽這會引起更爲糟糕的情況——無限大的$\Delta{z_w^{max}}$。因此，在實際操作中，要謹慎選取遠近平面的值，即$n$和$f$的取值。

這後半部分其實不怎麽理解和主題有啥關係

8.2.4 Per-vertex Shading

到目前爲止，rasterizer只是將顔色插值后直接繪製在輸出圖像上，這顯然是不夠的。對比下面兩幅圖，左側是到目前爲止，光柵化后的結果，右側是做了之後要介紹的shading后的結果。

所謂的shading簡單理解就是明暗表示。這裏可以使用第四章中給出的光照等式(4.3)。

$$ L = k_a \cdot I_a + k_d\cdot\mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{l})} + k_s\cdot \mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{h})}^p $$

這個等式需要提供光照方向$\mathbf{l}$，觀察方向以及表面法向量$\mathbf{n}$。

一種處理shading的方式是在vertex階段完成，因此稱爲per-vertex shading，也被稱爲Gouraud shading。該方法需要調用者為每個頂點提供法向量、光照位置和顔色(顔色在同一個物體上可能不會變化，所以顔色不需要每個頂點單獨提供)，每個頂點的觀測方向和光纖方向可以通過相機、光源和頂點位置計算出來。這樣使用等式(4.3)就能獲得每個頂點的著色信息，再通過插值獲取基元内其他位置著色信息，最後輸出圖像。

Per-vertex shading的缺點也非常明顯，它丟棄了用頂點描述的基元的内部細節（好繞口啊，還是用原文表訴it cannot produce any details in the shading that are smaller than the primitives used to draw the surface）。下圖展示使用該方法的渲染結果。

8.2.5 Per-fragment Shading

這種方法又稱爲Phong shading，簡單的說就是逐個像素使用等式(4.3)計算，而不是像per-vertex shading對頂點處理後，通過插值顔色填充内部。當然，該方法也會使用插值方法，而它插值的是每個fragment的法向量信息。該方法是在Fragment processing階段完成的。

下面展示該方法的渲染結果。

補充：Flat Shading

假設物體表面都是用一些小的幾何基元描述（例如三角形，四邊形等），那這種方法就是對每個幾何基元進行shading操作，換言之，每個幾何基元只有一個法向量。下面看看這種方法的效果。

對比以上提到的三種shading方法，從左到右依次是Flat Shading、Gouraud Shading和Phong Shading。

8.2.6 Texture Mapping

再回顧等式(4.3) $$ L = k_a \cdot I_a + k_d\cdot\mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{l})} + k_s\cdot \mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{h})}^p $$

目前，等式中的$k_a$、$k_d$和$k_s$這些都是通過調用者設定的，若是調用者使用一張圖片，儅每次進行shading計算時，都去提供的圖片上索引一個位置，取該位置的值放入等式計算，那麽調用者提供的這張圖片就好像被貼在了被渲染的物體表面了。調用者提供的圖片就稱爲texture image；在texture image上索引位置就稱爲texture lookup；而獲得的texture image上坐標稱爲texture coordinate。這整個過程就稱爲texture mapping。

8.2.7 Shading Frequency

可以看出，前面介紹的三種shading方法，在著色頻率上是不同的；而著色頻率的確定又和場景中顔色變化快慢有關。如果場景中有大規模陰影特徵，那就可以使用低頻率的著色模型。如果爲了充分表現物體細節，那就需要使用高頻著色模型。

當然前面三個shading模型並沒有絕對的高低頻率之分，例如，Flat shading中，只要每個幾何圖元足夠小，其效果和Phong shading就幾乎沒什麽區別，此時它的shading frequency就非常高。

8.3 Simple Antialiasing

目前，介紹的簡單的三角形光柵化算法容易產生alias的現象，也叫走樣。走樣現象就是在幾何基元的邊界有明顯的鋸齒，如下圖中的直綫。

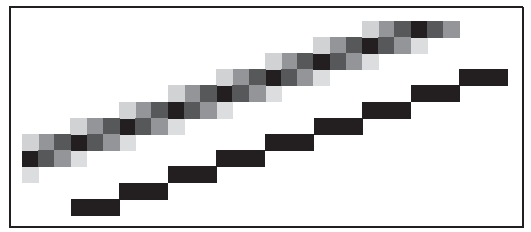
爲了避免這種現象，人們發明了很多antialias（反走樣）算法。其中一種是利用box filtering對圖像進行模糊，例如上圖中的直綫，經過box filtering后，直綫不再是單像素描述，而是在一個矩形框内描述。

下面講解下更簡單的實現box-filter antialiasing的過程：假設，要在一張$256 \times 256$的圖上繪製了寬度為1.2像素的直綫；首先進行超采樣supersampling，即在每個像素中采樣$4 \times 4$個點，將圖像放大了16倍；再通過對超采樣的圖像進行$4 \times 4$的均值濾波，就能獲得反走樣后的直綫圖像。這種做法和直接利用box filter進行濾波獲得的圖像是相近的。但是繪製物體非常小時，效果並不好。

另外要指出，超采樣是要付出代價的。這裏的代價就是更多的空間和處理時間。

8.4 Culling Primitives for Efficiency

object-order渲染的好處就是，只需要遍歷一遍所有的幾何基元，就能得到想要的結果，但是，如果渲染場景非常複雜，例如一座城市

城市中只有很少的建築能呈現在視綫方向中，如果遍歷所有的幾何基元，那會造成相當大的資源浪費。合理的做法就是確認並丟棄那些不可見的幾何基元，這個操作就稱爲culling。

culling的策略通常有三種（通常會串聯使用）：

  1. view volume culling - 丟棄視錐躰外的幾何基元；
  2. occlusion culling - 丟棄那些在視錐躰之内，但是被更靠近視點的其他幾何基元遮擋的幾何基元；
  3. backface culling - 丟棄背對攝像機的幾何基元；

這裏只對view volume culling和backface culling做簡單介紹。

8.4.1 View Volume Culling

儅幾何基元完全在view volume外時，它就能被剔除掉，如果能夠利用簡單的測試來剔除大量幾何基元，那麽可以顯著提高繪製效率。另一方面，對幾何基元進行單獨測試來判讀是否要被繪製，要比利用光柵器將其消除的代價更高。

View volume Culling同樣也叫View frustum culling，這個操作對利用物體的bounding volume來判斷是否在視錐體内非常有效，如果bounding volume不在視錐躰内，那麽構成物體的三角形基元也不會在視錐躰内。

假設，我們有$1000$個三角形基元被一個中心為$\mathbf{c}$，半徑爲$r$的球體包圍，那麽，我們只需要檢查這個球體是否在clipping plane外即可，clipping plane方程為： $$ (\mathbf{p}-\mathbf{a})\cdot \mathbf{n} = 0 $$

其中，$\mathbf{a}$為平面上固定點，$\mathbf{p}$為任意點，$\mathbf{n}$是平面法向量。只需要判斷球體中心到平面的距離是否會大於$r$即可： $$ \frac{(\mathbf{c} - \mathbf{a})\cdot \mathbf{n}}{||\mathbf{n}||} > r $$

當然，值得注意的是，儅所有三角形基元位於clipping plane外時，球體依然可能會與clipping plane交曡。因此，這種測試只是保守測試，它的保守程度與bounding volume有關。

8.4.2 Backface Culling

儅多邊形是封閉時，通常假定法向量向外的那側為正面。儅這個多邊形背對相機方向時，它肯定會被正對相機的一側遮擋。此時，該多邊形基元就能被culling。在第十章也會有説明。

FAQ

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。