在圖形學中，經常需要處理連續函數，但是，計算機只能處理離散的數據，通常的做法就是將連續函數離散化后交給計算機處理，之後在重建出連續函數。生活中也有許多離散化的例子，例如數碼相機拍照、手寫數位板以及CT掃描等。

本章將先從一維數字信號的采樣和重建。然後介紹一維和二維采樣和重建背後的數學原理和算法。最後將從頻域的角度深入討論。

9.1 Digital Audio: Sampling in 1D:

先來看個有關聲音的例子：

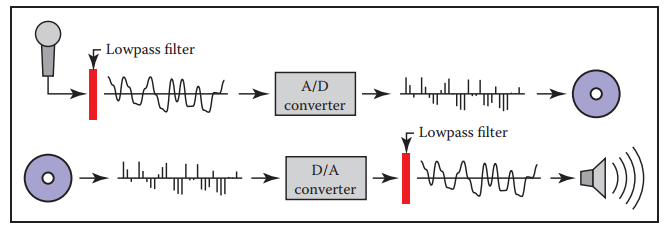
從麥克風中產生連續的聲音信號，經過A/D轉換器(analog-to-digital converter)后，成爲離散信號記錄在存儲裝置内。之後想從存儲裝置中復原聲音，需要利用D/A轉換器(digital-to-analog converter)，將離散信號恢復成連續信號，交給喇叭播放出來。

事實證明，A/D轉換過程中采樣率往往由高音決定；較低的頻率在再現高頻聲音時會出現降采樣失真（undersampling artifacts）現象。爲了消除這個現象，在將信號進行A/D轉換前，需要進行濾波操作，消除可能引起問題的高頻信號。

另一個現象是，D/A轉換器輸出的電信號在不處理前是呈現階梯狀的，這種階梯信號會引入嗡嗡的噪聲，這是所謂的（reconstruction artifact）。爲了消除這個現象，播放器在接受到D/A轉換的信號后，同樣需要進行濾波，用以平滑波形，消除階梯。

9.1.1 Sampling Artifacts and Aliasing

上面提到的聲音的兩種失真現象同樣會出現在圖像和圖形學中其他和采樣相關的地方。而解決方案也和聲音信號處理一樣：采樣前進行濾波以及重建信號時再進行濾波。

這節重點看看采樣過程中的失真(走樣)現象。如下圖所示：

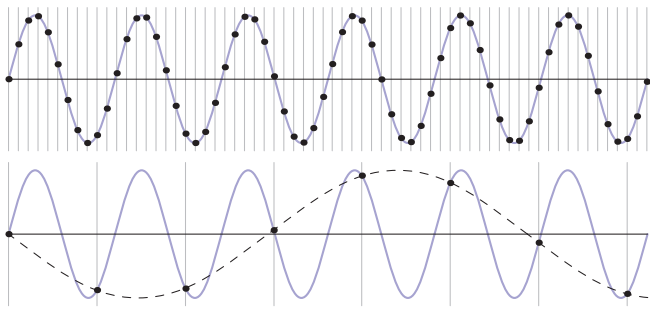
對比圖中上下兩種采樣頻率結果，上面的采樣頻率是每個周期采樣$10.8$次，下面的是每個周期采樣$1.2$次。顯然是采樣頻率高的更能反映原始信號的樣子，而較低的采樣頻率已經無法反映原始信號。這種無法如實反映原始信號的采樣結果就稱爲走樣(alias)。

圖像中的走樣現象，通常會表現出“摩爾紋”(moire pattern)，另一個現象就是直綫上出現“鋸齒”。如下圖所示：

采樣和重建的一些定量問題現在還非常難回答，比如：

  1. 采樣頻率多高才能保證獲得較好的結果？
  2. 哪些濾波器適合采樣和重建？
  3. 多少程度的平滑才能消除走樣現象？

這些問題的回到需要到9.5節后才能給出。

9.2 Convolution

在介绍后面内容前，先介绍一个数学工具——卷积（convolution），并约定符号 $ \star $ 表示卷积运算，例如 $ f \star g$ 表示函数$f$与函数$g$进行卷积运算。

卷积运算可以运用于连续函数，也可以运用于离散函数；可以用于一维、二维，也可以用于高维。所以这个运算非常重要（务必掌握）。这里先从离散一维情况开始，再到一维连续函数，最后拓展到二维或三维情况。

9.2.1 Moving Averages

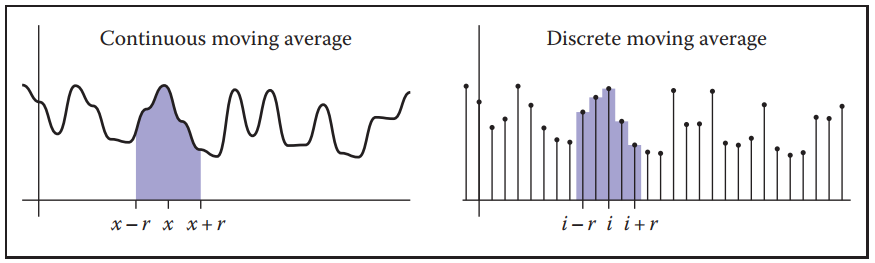
moving averages操作如下：计算函数在点$x$处，半径为$r$的范围内的均值。该操作能够对数据起到平滑作用，而半径$r$则是控制平滑程度的超参数。用数学表示moving averages如下： $$ h(x) = \frac{1}{2r}\int_{x-r}^{x+r}g(t)dt $$

对于离散情况： $$ c[i] = \frac{1}{2r + 1}\sum_{j=i-r}^{i+r}a[j] \tag{9.1} $$

从数学表示中可以看出，如果是对一个常数函数进行该操作，那么结果依然是原常数函数（定义域为$(-\infty, +\infty)$）。另外，moving average就是一个简单的卷积，两者不同的是，卷积是一种带权的移动平均。

9.2.2 Discrete Convolution

假设一个离散序列$a[i]$与另一个离散序列$b[i]$进行卷积运算，结果用$(a\star b)[i]$表示。 $$ (a \star b)[i] = \sum_{j}a[j]b[i-j] \tag{9.2} $$

结合图片：

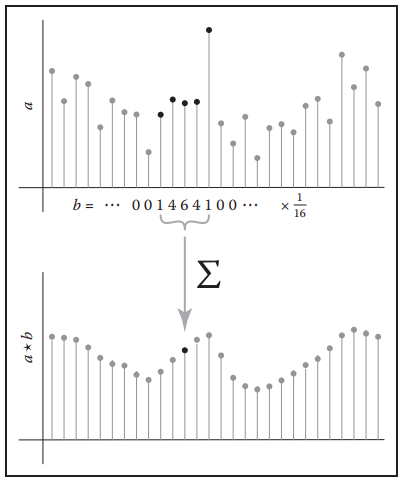
公式(9.2)中，需要将$a$序列当作权重序列，而$b$序列当作源序列。这里还要注意，卷积运算其实有对源序列进行一个倒序的操作，而相对的没有倒序的类似运算叫做相关。下面给出冈萨雷斯《Digital Image Processing》一书中两者运算对比图。

通常，$a$、$b$序列都不是无穷区间的，这里假设序列$b$在$|k| > r$时，$b[k] = 0$。这样公式(9.2)就可以在有限区间上表示： $$ (a \star b)[i] = \sum_{j=i-r}^{i+r}a[j]b[i-j] $$

这样，卷积的算法框架就很清晰了：

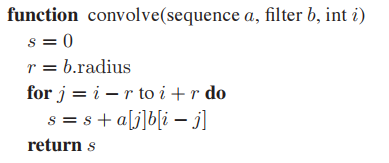
Convolution Filters

以之前的moving average操作爲例，其使用的濾波器為box filter，“盒”滤波器——在確定的區間内，每個點權重一樣，而在區間外權重均爲零。

$$ b[k] = \begin{cases} \frac{1}{2r+1} & -r \leq k \leq r \\[2ex] 0 & \text{otherwise} \end{cases} $$

將box filter帶入等式(9.2)，化簡后就可得到moving average的等式(9.1)。

濾波器捲積核通常是需要精心設計的，例如本例中，濾波器捲積核的縂權重為$1$，這樣就不會影響信號的整體水平。

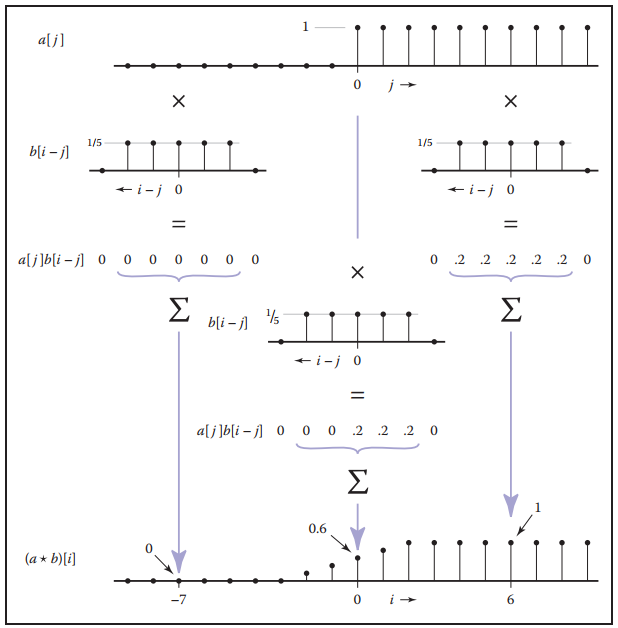
舉例，假設有一個階躍函數$a[i]$和盒濾波器$b[k]$：

$$ \begin{align} a[i] &= \begin{cases} 1 & i \geq 0, \\ 0 & i < 0, \end{cases} \\[2ex] b[k] &= \frac{1}{5}\begin{cases} 1 & -2 \leq k \leq 2, \\ 0 & \text{otherwise}. \end{cases} \end{align} $$

兩者之間做捲積的結果如下：

Properties of Convolution

  1. 捲積運算滿足交換律
$$ (a \star b)[i] =\sum_{j}a[j]b[i-j] = \sum_{k}b[k]a[i-k] = (b \star a)[i] $$

  1. 捲積運算滿足結合律： $$ (a \star (b \star c))[i] = ((a \star b) \star c)[i] $$

  2. 捲積運算滿足分配律： $$ (a \star (b + c))[i] = (a \star b + a \star c)[i] $$

因爲有這些特性，捲積運算可以先將捲積核閒先進行運算，之後再與源數據進行捲積，這種操作可以大大提高運算效率。例如：$((a \star b_1) \star b_2) \star b_3 = a \star (b_1 \star b_2 \star b_3)$

此外，還有一個簡單又特別的捲積核，identity filter，其定義如下：

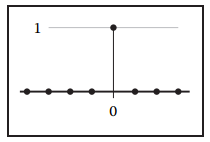
$$ d[i] = \begin{cases} 1, & i = 0 \\ 0, & \text{otherwise}. \end{cases} $$

這個捲積核的作用與單位矩陣$\mathbf{I}$類似： $$ (a \star d)[i] = \sum_{j = i}^{j = i}a[j]d[i-j] = a[i] $$

因此，這個捲積核在簡化一系列捲積運算時，起到非常重要的作用。例如： $$ c = a - a \star b = a \star d - a \star b = a \star (d - b) $$

9.2.3 Convolution as a Sum of Shifted Filters

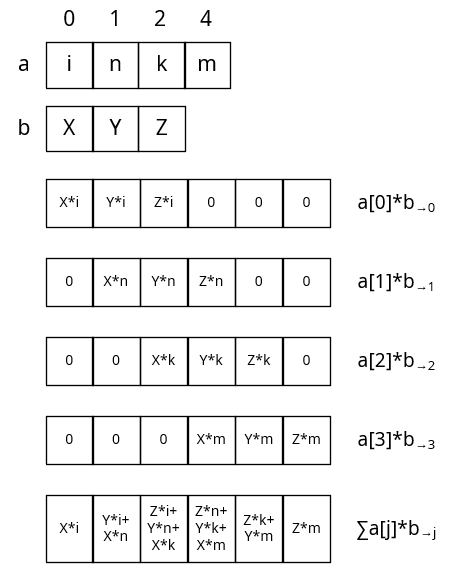
前面利用帶權重的moving average來解釋捲積運算，現在換個解釋方式。假設忽略$[i]$，將$b[i-j]$表示為平移形式$b_{\rightarrow j}[i] = b[i - j]$，那麽公式(9.2)可改寫爲： $$ (a \star b) = \sum_{j}a[j]b_{\rightarrow j} $$

舉個例子來理解這個表示形式（書上的例子非常不直觀，反正一開始是沒看懂）。

9.2.4 Convolution with Continuous Functions

連續函數的數學定義： $$ (f \star g)(x) = \int_{-\infty}^{+\infty}f(t)g(x - t) dt \tag{9.3} $$

連續函數$f$和$g$的捲積是兩函數乘積曲綫下所圍的面積，如下圖所示。

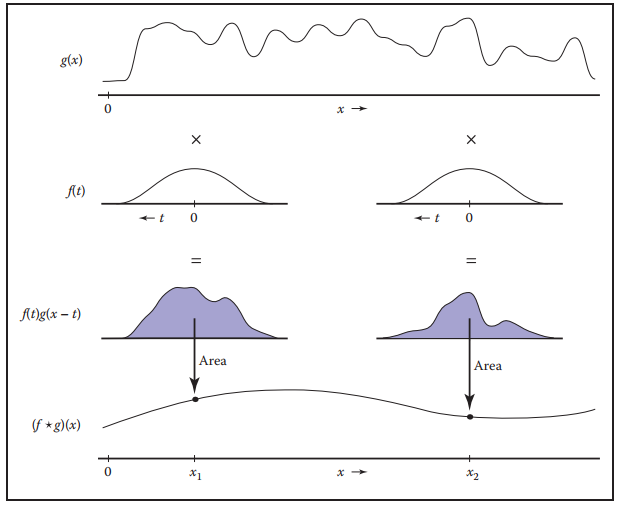
同離散捲積一樣，連續函數的捲積同樣滿足交換律和分配律；同樣也能用shift的形式表示： $$ (f \star g) = \int_{-\infty}^{+\infty}f(t)g_{\rightarrow t}dt $$

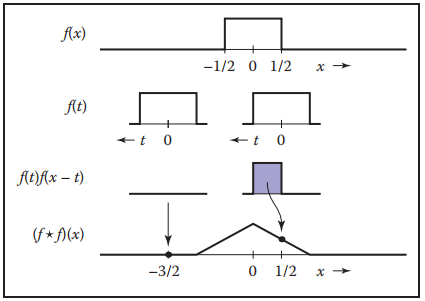
下面列舉幾個常用的捲積函數。例如box function

$$ f(x) = \begin{cases} 1, & -\frac{1}{2} \leq x < \frac{1}{2} \\ 0, & \text{otherwise} \end{cases} $$

將兩個box function做捲積會得到另一個常用的tent function。

$$ (f \star f)(x) = \begin{cases} 1 - |x|, & -1 < x < 1\\ 0,& \text{otherwise} \end{cases} $$

最後是一個非常常用的函數，其作用類似矩陣中的單位矩陣$\mathbf{I}$，這個函數就是Dirac Delta Function，用符號$\delta(x)$表示，其圖像如下。

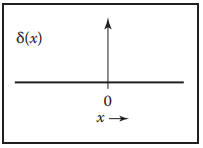
該函數的特點是：只在$x = 0$有值（該值可以認爲是$+\infty$），且有無窮小的寬度，但其面積始終為$1$。因此利用該函數與其他函數做捲積運算可得： $$ \int_{-\infty}^{+\infty}\delta{(x)}f(x)dx = f(0) $$

在看個Delta函數與其他函數捲積的效果：

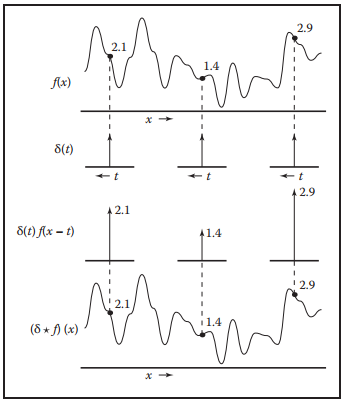
這個例子可得出： $$ (\delta \star f)(x) = \int_{-\infty}^{+\infty}\delta{(t)}f(x-t)dt = f(x) $$

即，$(\delta \star f) = f$。

9.2.5 Discrete-Continuous Convolution

連接離散空間和連續空間的方式有兩種，其中一種是采樣，將連續函數離散化，就是取出連續函數中所有整數位置的值即可。 $$ a[i] = f(i) $$

另一种方式是重建，從離散序列中恢復出連續函數。采用的方法是，利用連續濾波器$f(x)$對離散序列$a[i]$進行濾波操作。 $$ (a \star f)(x) = \sum_{i}a[i]f(x-i) $$

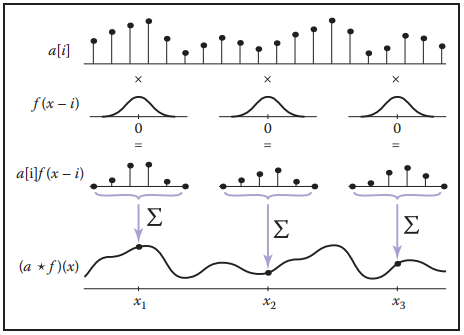
若知道了濾波器的半徑$r$，就能對離散捲積運算定界，因此上式可表示爲： $$ (a \star f)(x) = \sum_{i = |x -r|}^{|x + r|}a[i]f(x - i) $$

重建過程的代碼架構如下：

離散-連續捲積與樣條曲綫緊密相關。對於均匀樣條曲綫（例如，B樣條曲綫），其參數化曲綫恰好是樣條曲綫的基函數與控制點序列的捲積。

9.2.6 Convolution in More than One Dimension

之前的介紹都是在一維空間下進行，現在拓展到二維空間，離散捲積表示如下： $$ (a \star b)[i,j] = \sum_{i’}\sum_{j’}a[i’,j’]b[i-i’, j-j’] $$

若$b$是半徑爲$r$的濾波核（其有$(2r+1)^2$個值）。可用如下形式表示： $$ (a \star b)[i,j] = \sum_{i’ = i - r}^{i+r}\sum_{j'= j-r}^{j+r}a[i’,j’]b[i-i’, j-j’] $$

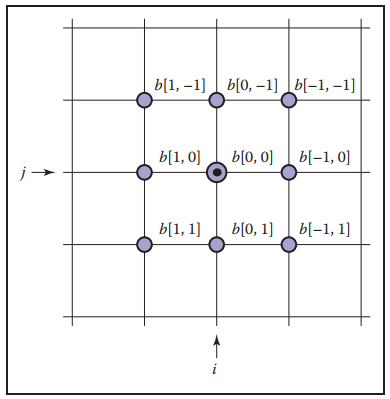
二維離散捲積框架如下：

對於連續函數的二維捲積與離散-連續函數的二維捲積表達如下：

$$ (f \star g)(x,y) = \iint f(x', y')g(x - x', y-y')dx'dy' \\[2ex] (a \star f)(x, y) = \sum_{i}\sum_{j}a[i,j]f(x - i, y - j) $$

對於更高維的捲積，可做類似拓展。

9.3 Convolution Filters

本節介紹一些圖形學中常用的捲積濾波器，以及這些濾波器的性質。

本節所定義的濾波器均有一個natural radius，所謂natural radius就是濾波器函數在natural radius内的圖像與坐標軸所圍成的面積始終為$1$。例如，box filter的natural radius為$\frac{1}{2}$；cubic filter的natural radius為$2$。這麽設定是爲了保證在采樣或重建過程中不改變信號的平均值。

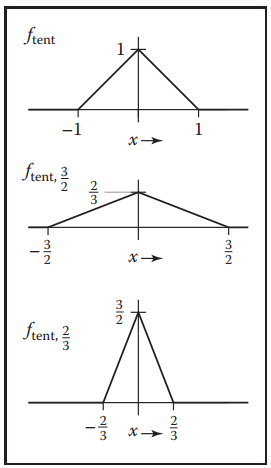
這裏對於基濾波器再定義一個縮放比率$s$，這樣就能獲得不同形狀的濾波器： $$ f_s(x) = \frac{f(x/s)}{s} $$

儅濾波器經過縮放比率處理，其natural radius也由原先$r$變爲$sr$。例如下圖中的tent filter。

The Box Filter

$$ a_{box,r}[i] = \begin{cases} 1/(2r+1), & |i| \leq r \\ 0, & \text{otherwise} \end{cases} $$
$$ f_{box,r}(x) = \begin{cases} 1/(2r), & -r \leq x < r \\ 0, & \text{otherwise} \end{cases} $$

該濾波器圖像

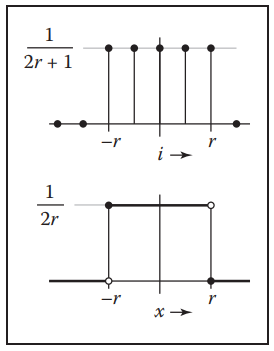
注意：對於連續形式的box filter，區間端點只包含了一側，這是爲了其能作爲重建濾波器使用，由於box filter是不連續的，所以在邊界處理要格外注意。

The Tent Filter

$$ f_{tent}(x) = \begin{cases} 1 - |x|, & |x| < 1 \\ 0, & \text{otherwise} \end{cases} $$

這個濾波器的離散形式就是在其連續形式下取整數位置的值即可，這裏就不單獨列出。tent filter的圖像如下：

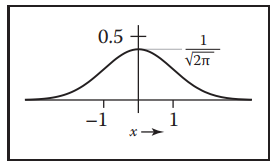
The Gaussian Filter

$$ f_{g,\sigma}(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-x^2/2\sigma^2} $$

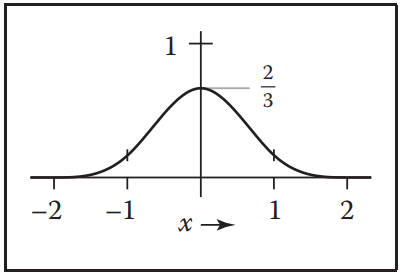
這個濾波器函數就是著名的``正態分佈``函數，其中$\sigma$表示標準差，該濾波器有非常好的采樣效果，因爲它非常平滑。但是它沒有特定的``natural radius``，它作用于$\sigma$的範圍内。通常使用過程中，會將高斯核的尾部進行裁剪（即某個半徑$r$外的值設爲零），這意味著濾波器的寬度和``natural radius``會隨著實際應用而變化。另外，按縮放比率$s$處理后裁剪的高斯核，與標準偏差為$s\sigma$和半徑為$sr$的未裁剪的高斯核是等價的。因此，在實際應用中，通常將$\sigma$和$r$設置為高斯濾波器的配置屬性。

The B-Spline Cubic Filter

B-Spline濾波器由分段函數表示，natural radius為$2$，具有二階連續性$\mathcal{C}^2$，通常用於重建。

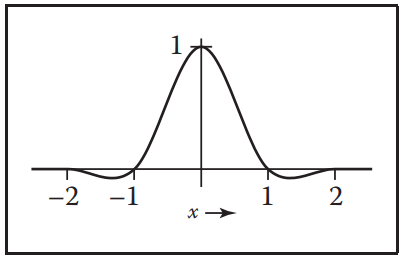
$$ f_B(x) = \frac{1}{6}\begin{cases} -3(1-|x|)^3 + 3(1-|x|)^2 + 3(1-|x|) + 1, & -1 \leq x \leq 1 \\[2ex] (2 - |x|)^3, & 1 \leq |x| \leq 2 \\[2ex] 0,& \text{otherwise} \end{cases} $$

另外，B-Spline濾波器可以表示為多個Box Filter的捲積： $$ f_B = f_{box} \star f_{box} \star f_{box} \star f_{box} $$

The Catmull-Rom Cubic Filter

該濾波器在$x = -2, -1, 1, 2$處取$0$值。

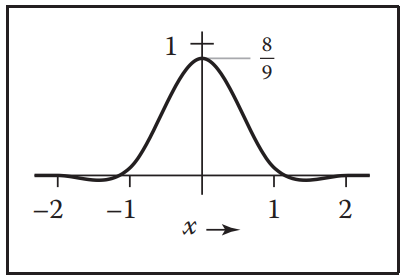
$$ f_C(x) = \frac{1}{2}\begin{cases} -3(1-|x|)^3 + 4(1-|x|)^2 + (1-|x|), & -1 \leq x \leq 1 \\[2ex] (2 - |x|)^3 - (2 - |x|)^2, & 1 \leq |x| \leq 2 \\[2ex] 0, & \text{otherwise} \end{cases} $$

The Mitchell-Netravali Cubic Filter

該濾波器是前面兩個樣條濾波器的加權組合，該濾波器在圖像重采樣中有重要作用。

$$ \begin{align} f_M(x) & = \frac{1}{3}f_B(x) + \frac{2}{3}f_C(x)\\[2ex] & = \frac{1}{18}\begin{cases} -21(1-|x|)^3 + 27(1-|x|)^2 + 9(1-|x|) + 1, & -1 \leq x \leq 1,\\[2ex] 7(2-|x|)^3 - 6(2-|x|)^2, & 1 \leq |x| \leq 2,\\[2ex] 0,& \text{otherwise}. \end{cases} \end{align} $$

9.3.2 Properties of Filters

一些滤波器有一些传统术语用于描述。

滤波器的脉冲响应（impluse response），它只是滤波器对仅包含一个脉冲信号的响应；

连续滤波器就是插值(interpolating)。例如用连续函数滤波器对离散点进行重建时，重建出的曲线会连接所有离散点，而不是在离散点附近拟合一条曲线；

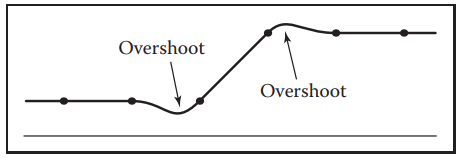
带有负值的滤波器存在振鈴或過冲現象，儅這種濾波器作用於劇烈變換的地方時，會引入額外的振蕩。下圖是Catmull-Rom濾波器對階躍信號進行濾波器的結果，可以很明顯的看到其最小(大)值，要比理想值來的小(大)。

儅連續函數濾波器用作重建時，如果它將恆定序列構建為常數函數（要求在所有整數位置的和為1，$\sum_if(x + i) = 1, \text{for all x}$），則説明該濾波器是ripple free的，在9.3.1節中除了Gaussian filter，其他濾波器在它們的natural radius中都是ripple free的（但在非整數範圍内時就不一定了）。如下圖所示。

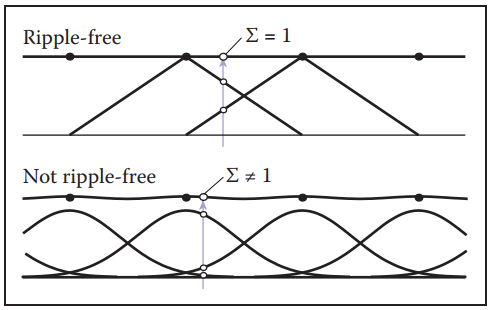
如果要消除離散-連續捲積中的ripple，方法也很簡單，只要將每個采樣位置的值除以權重和即可： $$ \overline{(a \star f)}(x) = \frac{\sum_ia[i]f(x-i)}{\sum_ia[i]} $$

連續函數濾波器還有一個連續度的概念，degree of continuity，即最高可導次數。用符號$C^n$表示，例如box filter是不連續的，tent filter一階導數不連續，所以稱爲零階連續，記爲$C^0$；B-spline filter是二階連續，記爲$C^2$；….。濾波器的連續性對於重建時非常重要，因爲重建后的函數的連續性與濾波器連續性相同。

Separable Filters

可分離濾波器主要是針對一維以上的濾波器的。這裏以二維濾波器爲例説明。假設，有二維濾波器$f_2(x,y)$，若其能分解爲如下形式，這該濾波器就是可分離的；

$$ f_2(x,y) = f_1(x)f_1(y) \\[2ex] b_2[i,j] = b_1[i]b_1[j] $$

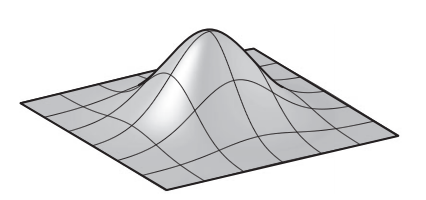
簡單説就是二維濾波器可拆成兩個方向的一維濾波器，則稱該二維濾波器可分離。常見的Gaussian Filter就是可分離的。

$$ \begin{align} f_{2,g}(x,y) & = \frac{1}{2\pi}(e^{-x^2/2}e^{-y^2/2}) \\ & = \frac{1}{2\pi}(e^{-(x^2 + y^2)/2}) \\ & = \frac{1}{2\pi}e^{-r^2/2} \end{align} $$

二維高斯函數圖像如下，其同時具有圓對稱和可分離的特性。

這還看不出可分離濾波器的好處，現在利用二維離散可分離濾波器$b_2$對一幅圖像$a$進行濾波：

$$ \begin{align} (a \star b_2)[i,j] & = \sum_{i'}\sum_{j'}a[i',j']b_1[i-i']b_1[j-j'] \\ & = \sum_{i'}b_1[i-i']\sum_{j'}a[i',j']b_1[j-j'] \\ & = \sum_{i'}b_1[i-i']S[i'] \end{align} $$

其中$S[i’] = \sum_{j’}a[i’,j’]b_1[j-j’]$。

可以看出，可分離濾波器可以讓時間複雜度從$\mathcal{O}(n^2)$下降到$\mathcal{O}(n)$。因爲從上面推導過程可知，圖像先沿著$j$方向進行一維捲積運算，其結果在沿著$i$方向進行一維捲積運算。而不是像一般二維捲積運算，要在每個位置都進行$[i,j]$方向的捲積。所以，可分離濾波器最大的好處就是提高運算效率。

下面給出可分離濾波器的代碼框架：

這裏忽略了邊界處理，邊界處理會在9.4.3節説明。

9.4 Signal Processing for Image

9.4.1 Image Filtering Using Discrete Filters

处理图像滤波时，最简单的是使用离散滤波器。例如，對圖像進行模糊操作，許多通用的低通濾波器都能實現。如下圖所示。從圖中可看出，高斯濾波器有非常平滑的模糊效果，所以這個濾波器也是模糊處理常用的。

與模糊操作相對的是“銳化”操作。其中一種方法是unsharp mask：從原始圖像中減去比率為$\alpha$的模糊圖像。

$$ \begin{align} I_{sharp} & = (1 + \alpha)I - \alpha(I \star f_{g,\sigma}) \\ & = I \star ((1 + \alpha)d - \alpha f_{g,\sigma})\\ & = I \star f_{sharp}(\sigma, \alpha) \end{align} $$

其中，$f_{g,\sigma}$為寬度為$\sigma$的高斯濾波器。這個銳化濾波器效果如下：

另一個例子是，物體投射陰影，對物體輪廓進行模糊和物體移位就可得到柔和的投影。如下圖所示。這裏用到的移位濾波器可表示爲：

$$ d_{m,n}(i,j) = \begin{cases} 1,& i = m \ \text{and}\ j = n \\ 0,& \text{otherwise} \end{cases} $$

整個投影濾波器：

$$ \begin{align} I_{shadow} & = (I \star d_{m,n}) \star f_{g,\sigma}\\ & = I \star (d_{m,n} \star f_{g,\sigma}) \\ & = I \star f_{shadow}(m,n,\sigma) \end{align} $$

9.4.2 Antialiasing in Image Sampling

前面已經提到過，在采樣過程中，如果采樣頻率遠低於信號頻率，那麽就會出現alias現象。這裏結合各種濾波器再進行説明。

在之前章節已經提到，走樣現象有兩種表現，一種是jaggies，一種是moire patterns。jaggies就是單像素直綫呈現出"鋸齒”狀；moire patterns就是出現一種連續樣式，如下圖中右圖的窗簾位置。

解決alias現象的一個方法是，對圖像模糊后再進行采樣。例如使用box filter進行模糊；但是這類濾波器雖然能提高銳化邊緣的效果，但是依然會產生摩爾紋。如下圖所示。雖然高斯濾波器可以得到更好的效果，但是它也使得圖像變得更模糊。這就需要使用者在銳化度和走樣之閒尋求一個平衡。

9.4.3 Reconstruction and Resampling

Resampling，是圖像處理中一個非常重要的操作，例如圖像縮放都屬於resampling操作。這個操作可以理解爲，對原始信號，利用連續函數重建后，在重建得到的連續函數進行重新采樣的過程。如下圖所示。

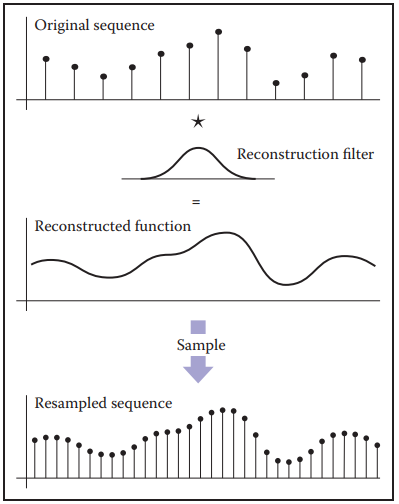
這樣就能得到重采樣的代碼框架。

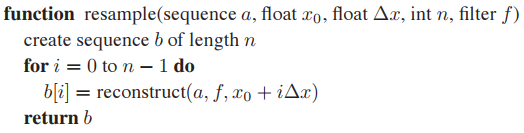
從上面過程分析，好像reconstruction和sampling是順序進行的，其實并非如此，重建后的連續函數只是理論上存在的，我們只需要直接計算重采樣位置上的值就行了，不一定要得到重建后的連續函數。另外，前面說要解決采樣過程中的走樣問題，需要在采樣前對信號進行模糊（平滑）。所以，整個Resampling過程可以變爲下圖所示的形式。

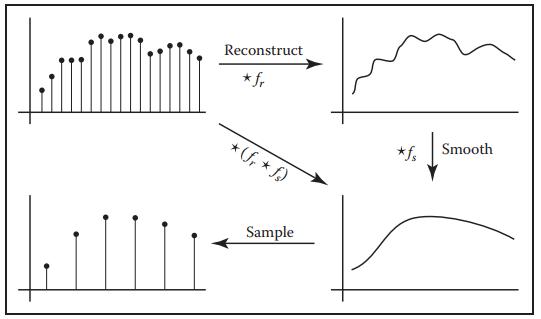
這樣，我們可以將重建濾波器、平滑濾波器和采樣濾波器三個濾波器合成一個resampling filter。

另外，重采樣圖像一般是運用在矩形區域内，假設原始圖像尺寸為$(x_l, x_h) \times (y_l, y_h)$，新圖像尺寸為$(n_x^{new}, n_y^{new})$，那麽$x$和$y$方向的采樣率分別為$\Delta{x} = (x_h - x_l) / n_x^{new}$和$\Delta{y} = (y_h - y_l)/n_y^{new}$。這樣，起始采樣位置為$(x_l + \Delta{x} / 2, y_l + \Delta{y} / 2)$。基於矩形範圍的采樣代碼框架如下。

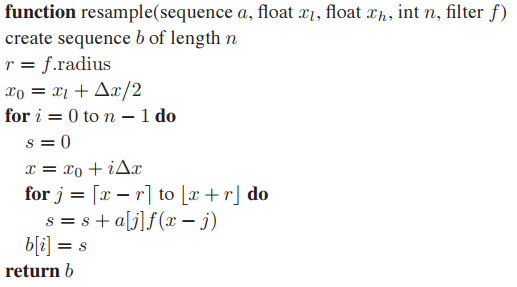
現在又遇到了邊界處理問題，這裏一起來説明下。通常邊界處理有以下幾種方式：

  1. 遇到超出邊界範圍的就截斷，相當於在圖像外圈填充了$0$值像素；

  2. 遇到超出邊界範圍，取離該邊界最近的像素值填充；這相當於在圖像外圍填充了最外側一圈的像素值；

  3. 儅遇到邊界時，修改濾波器以適應越界處理。

以上第一種方法，會導致圖像邊緣偏暗；第二種方法容易實現；第三種方法能獲得很好的效果，這種方法最簡單的處理是： $$ result = \frac{\sum_{j}f[j]a[x-j] * \sum_{i}f[i]}{\sum_{j}f[j]} $$

其中，$i$取值為整個濾波器尺寸範圍，$j$取值為落在圖像内的部分。儅$\sum_{i}f[i] =1$時，可以保證圖像的平均亮度。

另一個重要問題是：重采樣濾波器的選擇，一般有兩個参考方向：濾波器形狀和尺寸。從前面分析可知，重采樣濾波器不僅含有重建濾波器，還有采樣濾波器；對於重建濾波器，再放大圖像時，我們希望它足夠平滑來消除走樣現象，并且濾波器要是ripple free的；對於采樣濾波器，我們則希望濾波器尺寸足夠大，以消除降采樣過程中出現的摩爾紋。根據下圖展示，繼續説明。

当输出图像是输入图像的降采样时，采样滤波器的平滑程度要比重建滤波器的平滑程度来的大，所以要依据输出采样间隔来调整滤波器尺寸（如上圖中 $radius = 3$）；当对输出圖像需要更精细的采样（对图像进行向上采样或放大）时，重构所需的平滑度将占主导地位（重构函数已经足够平滑，可以比开始时更高的速率进行采样），因此 濾波器尺寸由输入样本间距确定（如上圖中 $radius = 1$）。

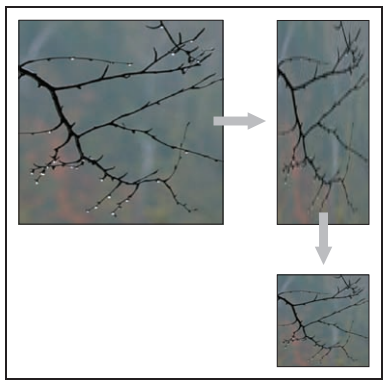
選擇濾波器的過程通常要權衡處理效率和處理質量。box filter速度最快，tent filter效果中等，piecewise cubic效果最好。在piecewise cubic中，一般Mitchell-Netravali filter是較好的選擇。另外，采用可分離濾波器也能顯著提高效率，可分離濾波器的本質相當於在行方向進行了重采樣（改變圖像寬度，不改變圖像高度）；再在列方向進行重采樣得到最後結果。如下圖所示。

9.5 Sampling Theory

先説明：第9.5節内容的梳理雖然惡補了很多知識，由於平常用的太少，在理解深度上還有所欠缺，本節内容大多數來自原書的翻譯，如果有些地方解釋不到位請指正。

9.5.1 The Fourier Transform

傅里葉變換和捲積是采樣理論的數學基礎。而傅里葉變換的基礎是，任意函數都能通過叠加不同頻率的正弦函數獲得。例如下圖所示，其展示了函數 $$ \sum_{n=1,3,5,\cdots}^{\infty}\frac{4}{\pi n}\sin{(2\pi n x)} $$ 叠加不同個數正弦波的結果。

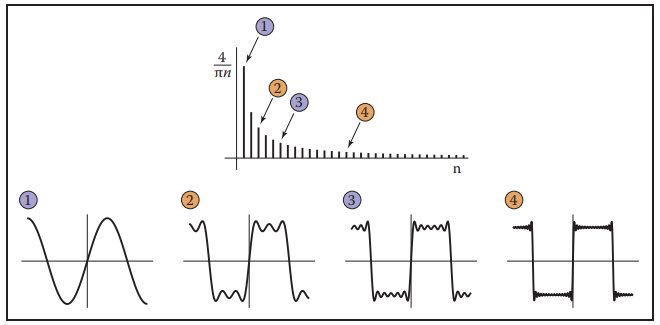
值得注意，正弦信號是周期性信號，而對於非周期信號采用這種方式表示，則需要叠加更多的正弦信號，相較於使用離散信號的叠加，采用連續正弦函數族的積分表示顯然更加合適。例如，盒函數(box function)，其可用餘弦函數族積分表示： $$ \int_{-\infty}^{\infty}\frac{\sin{(\pi u)}}{\pi u}\cos{(2\pi u x)}\mathrm{d}u \tag{9.6} $$

等式(9.6)表示，盒函數可由無窮多個不同的頻率的餘弦函數叠加而成，而不同頻率$u$的餘弦函數的振幅由函數$\frac{\sin{(\pi u)}}{\pi u}$決定(這裏的振幅也可理解爲每個餘弦函數的權重)。如下圖所示。

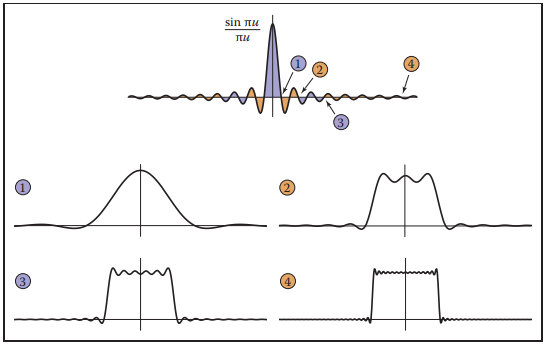
原始函數記爲$f$，振幅函數記爲$\hat{f}$。再利用歐拉公式可將等式(9.6)化簡為如下形式： $$ f(x) = \int_{-\infty}^{\infty}\hat{f}(u)e^{2\pi i u x}\mathrm{d}u \tag{9.7} $$

等式(9.7)稱爲傅里葉逆變換(inverse Fourier transform (IFT))。其中函數$\hat{f}$告訴我們如何通過對一系列正弦函數積分來獲得原始函數$f$。函數$\hat{f}$取值稱爲傅里葉頻譜(Fourier spectrum)。

有傅里葉逆變換，必然有(正向)傅里葉變換((forward) Fourier transform (FT))，而傅里葉變換形式也非常簡單。 $$ \hat{f}(u) =\int_{-\infty}^{\infty}f(x)e^{-2\pi i u x}\mathrm{d}x \tag{9.8} $$

使用$f-\hat{f}$形式表示兩種變換有時并不方便，所以，經常會使用$\mathcal{F}\{f\}$和$\mathcal{F}^{-1}\{\hat{f}\}$表示傅里葉變換和傅里葉逆變換。

$$ \hat{f}(u) = \mathcal{F}\{f(x)\} \\[2ex] f(x) = \mathcal{F}^{-1}\{\hat{f}(u)\} $$

傅里葉變換有如下幾個性質：

  1. 一個函數和其傅里葉變換有相同的平方積分； $$ \int(f(x))^2\mathrm{d}x = \int(\hat{f}(u))^2\mathrm{d}u $$
  1. 原函數值縮放$a$倍，則其傅里葉變換也縮放$a$倍；
$$ \mathcal{F}\{af\} = a\mathcal{F}\{f\} $$
  1. 原函數若沿著自變量$x$方向上進行縮放$b$倍，則傅里葉變換將沿著$u$軸變化相同比例；
$$ \mathcal{F}\{f(x/b)\} = b\hat{f}(bu) $$
  1. 原函數的平均值等於$\hat{f}(0)$；
  1. 如果函數$f$是一個實數函數，則$\hat{f}$是偶函數($\hat{f}(u) = \hat{f}(-u)$)；類似，如果函數$f$是一個偶函數，則$\hat{f}$則爲實數函數。

以上只是簡單介紹傅里葉變換和傅里葉逆變換，如想更詳細瞭解其數學理論，可自行查閲相關書籍。

9.5.2 Convolution and the Fourier Transform

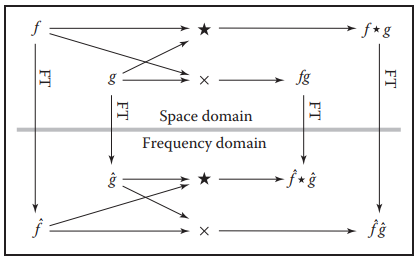
傅里葉變換和捲積運算之所以重要，是因爲兩者結合使用，能大大簡化運算。假設兩個函數$f$和$g$，它們的傅里葉變換為$\hat{f}$和$\hat{g}$，他們之間的捲積運算有如下方式：

$$ \mathcal{F}\{f \star g\} = \hat{f}\hat{g} \\[2ex] \hat{f}\star\hat{g} = \mathcal{F}\{fg\} $$

換而言之，就是，兩函數在時域中的捲積的傅里葉變換與兩函數頻域中的乘積相等；兩函數頻域中的捲積與時域中乘積的傅里葉變換相等。這個特性讓傅里葉變換在信號的采樣和重建上非常實用。原來這兩個操作都是在時域内進行運算，而傅里葉變換則告訴我們，在頻域中運算也能得到相同結果，而且運算方式只是簡單的乘法。如下圖所示。

這裏給出9.3.1節中提到的函數的傅里葉變換結果，並畫出他們的圖像。

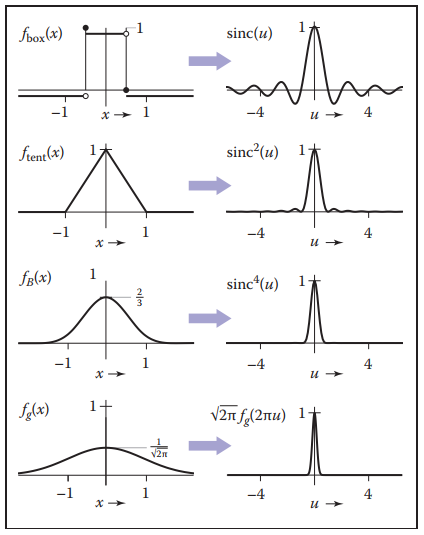
$$ \begin{align} \mathcal{F}\{f_{box}\} &= \frac{\sin{(\pi u)}}{\pi u} = \mathrm{sinc}{(\pi u)} \\[2ex] \mathcal{F}\{f_{tent}\} &= \frac{\sin^2{(\pi u)}}{\pi^2 u^2} = \mathrm{sinc}^2(\pi u) \\[2ex] \mathcal{F}\{f_{B-spline}\} &= \frac{\sin^4{(\pi u)}}{\pi^4 u^4} = \mathrm{sinc}^4(\pi u) \\[2ex] \mathcal{F}\{f_{Gaussian}\} &= e^{-(2 \pi u)^2/2} \end{align} $$

注意，高斯函數的傅里葉變換相當於將原先標準差為$1.0$的高斯函數變爲標準差為$\frac{1}{2\pi}$的高斯函數。

9.5.4 Dirac Impulses in Sampling Theory

脈衝信號在采樣理論中有重要作用，因爲它能夠對連續函數進行離散化。假設要表示一個在位置$a$処，信號强度為$b$的信號，則用脈衝信號可表示為$b\delta{(x - a)}$。因爲有這種特點，黨對一個連續函數$f(x)$進行離散化時，就能夠寫成$f(a)\delta{(x-a)}$。

在一系列等間距點上對函數進行采樣可以表示為原始函數乘以等間距脈衝信號的總和，這稱爲脈衝序列(impluse train)。假設脈衝序列周期為$T$，則： $$ s_T(x) = \sum_{i = -\infty}^{\infty}\delta(x - Ti) $$

下圖展示了不同周期的脈衝序列及其傅里葉變換。

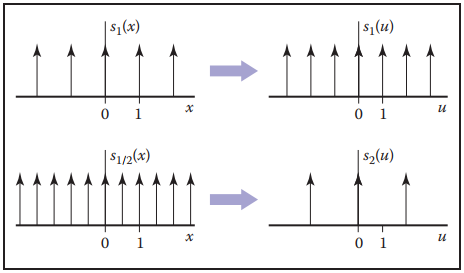
由傅里葉變換的性質可知，一個周期為$T$的脈衝序列的傅里葉變換結果是周期為$\frac{1}{T}$的脈衝序列。換而言之，在時域中采樣頻率越高，在頻域中表示則距離越遠。

9.5.5 Sampling and Aliasing

這裏從頻域角度解釋采樣和重建過程爲什麽需要捲積濾波操作，也可以解釋走樣（alias）現象。下面以圖像爲例，給出其采樣和重建后的頻譜。

figure9.48

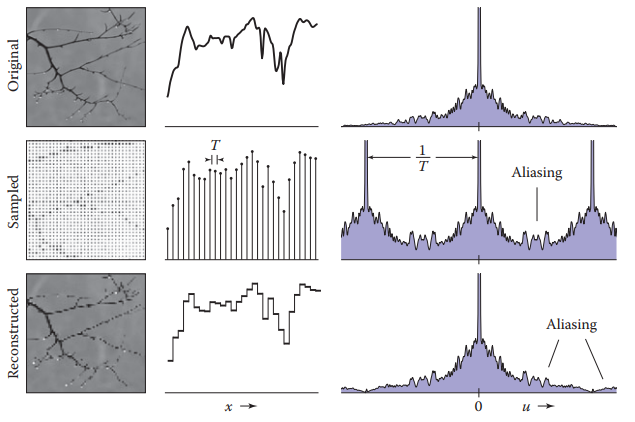
對於采樣操作，假設原始信號為$f$，采用脈衝序列$s_{T}$對其進行采樣，那麽計算方式為$f \cdot s_T$，由傅里葉變換的乘積-捲積性質可得采樣后信號的傅里葉變換為$\hat{f} \star \hat{s}_T = \hat{f} \star s_{\frac{1}{T}}$。利用脈衝序列$\delta$的定義可得： $$ (\hat{f} \star s_{\frac{1}{T}})(u) = \sum_{-\infty}^{\infty}\hat{f}(u - i / T) $$

從上式可以看出，與脈衝序列捲積結果，相當於在頻域上將原始信號的頻譜等間距$\frac{1}{T}$複製了N份。這導致在整數倍采樣頻率上很難在找到原始頻譜，因爲發生了混叠現象，這種現象是因爲原始信號頻率超過采樣頻率的一半（采樣頻率過低），這樣在混曡區域，信號不可逆的混合在一起，這就引起了走樣現象。這是走樣現象的第一種形式。這裏我們稱原始頻譜為基頻譜(base spectrum)，而那些複製頻譜稱爲走樣譜(alias spectra)。

下面從重建角度展示走樣現象的第二種形式。假設原始離散信號為$a$，現使用寬度為$1$的box filter$f_{box,\frac{1}{2}}$對其進行捲積。則，重建后的頻譜等於原始信號頻譜與box filter函數頻譜的乘積——$\hat{a} \cdot \hat{f}_{box,\frac{1}{2}}$。從上圖中可以看出，重建前後，基頻譜的高頻分量被一定削弱，而走樣譜也存在一定削弱，另外由於box filter函數有非常寬的頻譜，因此這些被削弱的走樣譜變得更突出。這就引起了第二種形式的走樣——由於重構濾波器不合適帶來了走樣。

這部分感覺好繞，原文寫的也很繞，而且從書中的圖對比看，不放大其實看不到什麽區別，另外還可能是對頻譜理解不深導致的。。。後期要有新體會再改改這部分

Preventing Aliasing in Sampling

從上面的分析可以看出，要想獲得效果較好的采樣或重建結果，所使用的濾波器需要精心挑選。對於采樣過程，從頻域角度上看，使用低通濾波器可以限制頻譜的範圍，可以有效地抑制信號的混曡現象。

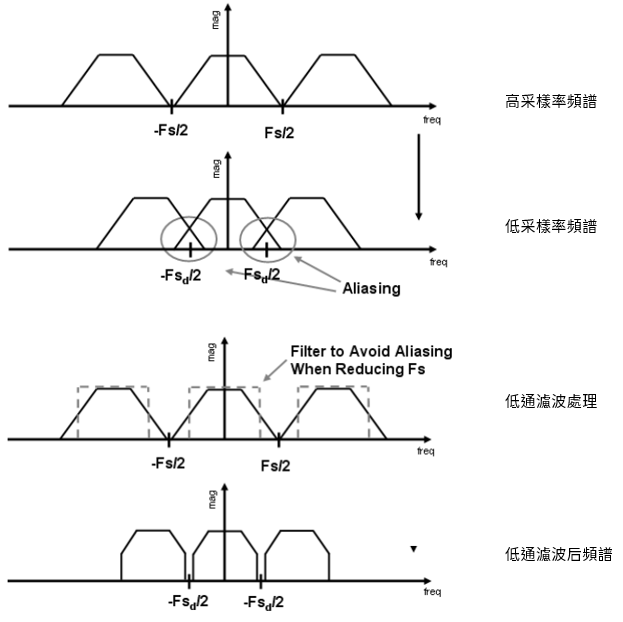
另外，提高采樣率也能避免混曡現象的發生，因爲高采樣率讓走樣譜之間裏的更遠。如下圖所示。

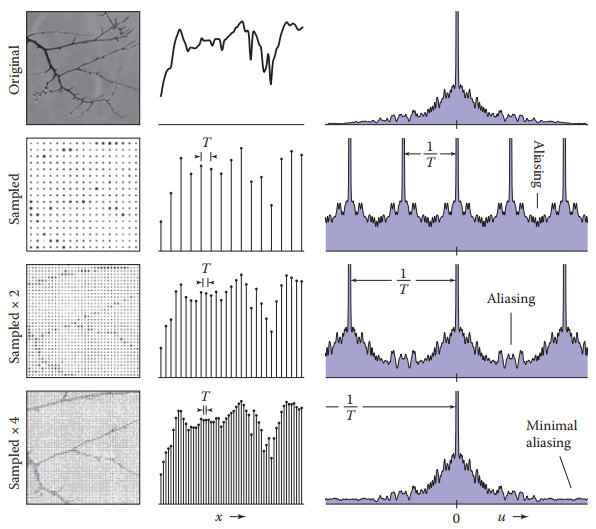
這兩種方法的原理都是讓頻譜寬度小於走樣譜之間的距離，換而言之，信號中最高頻率必須要小於采樣頻率的一半，這就是經典的奈奎斯特準則(Nyquist criterion)。通過采樣頻率所得到的最高允許頻率成爲奈奎斯特頻率(Nyquist frequency)或奈奎斯特極限(Nyquist limit)。根據Nyquist-Shannon采樣理論，頻率不超過奈奎斯特極限的信號（或者説帶寬限制為奈奎斯特頻率的信號），原則上可以根據樣本進行準確重構。

以上解釋説明，儅采樣頻率足夠高時，我們不需要使用采樣濾波器進行預處理，直接進行采樣就行。但是儅原始信號頻譜範圍非常廣，例如圖像中有銳利的邊緣時，這就必須使用采樣濾波器對帶寬進行限制。例如下圖中，不同濾波器對帶寬限制的效果。

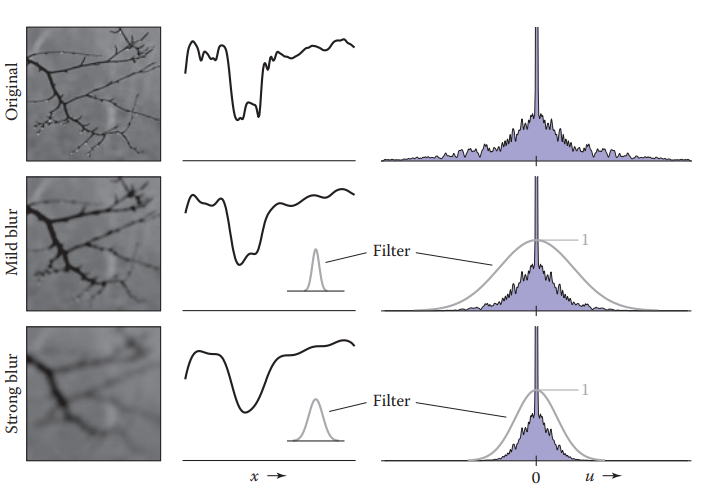
下圖展示了，在不同濾波器處理後，相同采樣率下獲得采樣圖像效果。

可以看出，低通濾波器雖然限制了頻譜寬度，但是它也讓圖像損失了高頻信息（就是讓圖像模糊了），但有時候這是值得的，因爲損失高頻信息總比得到混亂的頻譜來的好。

Preventing Aliasing in Reconstruction

從頻域角度看，重建濾波器的任務是剔除走樣譜，保留基頻譜。從圖9.48中可以看出，即使使用“粗糙”的重建濾波器，它也移除了走樣譜。重要的是，濾波器完全阻止了所有走樣譜的直流尖峰信號。這是所有合理的重建濾波器的特徵：在頻域空間中，在采樣頻率的倍頻処都有零值。事實證明，這個特點與時域上的ripple-free性質是等價的。所以，好的重建濾波器必須好的低通濾波器，它必須完全剔除倍頻処的頻率。

下圖展示了不同濾波器的重建效果。

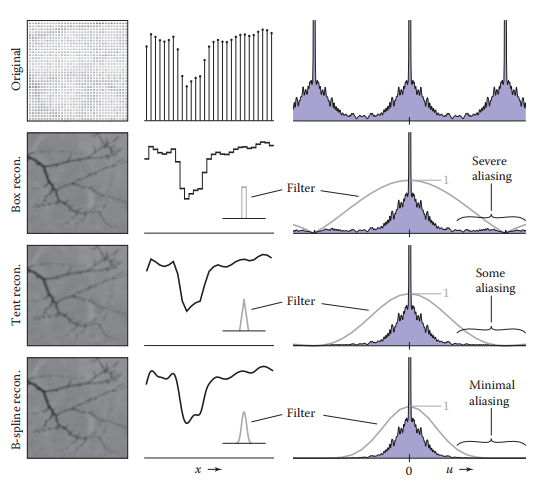
從圖中對比看，box filter是效果最差的，即使采樣率足夠高，但是依然會存在artifacts，也就是重建后的曲綫不夠平滑。而使用tent filter，相當於采用綫性插值，雖然削弱了高頻信號，但并沒有box filter那麽明顯的artifacts，重建后的曲綫也變得相對平滑。而最後的B-spline filter，重建曲綫非常光滑，有效的控制了走樣譜，還對基頻譜進行了一定程度的平滑，這就是之前提到的平滑和走樣之間的權衡。

Preventing Aliasing in Resampling

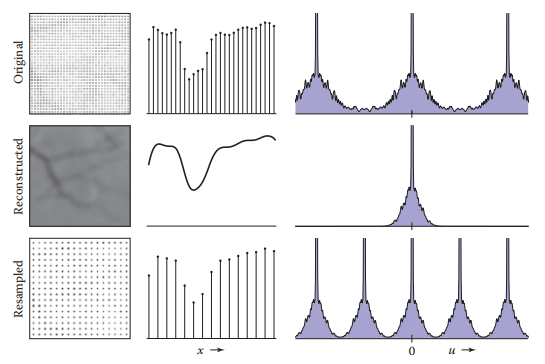
Resampling操作在之前説過，是Reconstruction和Sampling操作的結合，因此，之前提到反走樣的方法同樣適用重采樣操作，區別在於重采樣過程只使用了一個濾波器（同時要重建和采樣）。下圖展示了一個重采樣濾波器如何有效的剔除走樣譜，并且抑制頻譜寬度進行新的采樣操作。

9.5.6 Ideal Filters vs. Useful Filters

從頻域分析角度可得到一個結論：頻域中的盒濾波器(box filter)是采樣與重建的理想濾波器。在这两种操作下，该滤波器都能有效防止走样现象，而且不用减少Nyquist frequency之下的频率范围。

我們知道傅里葉變換和傅里葉逆變換在本質上是相同的，因此傅里葉變換為box filter的空域濾波器就是$sinc(\pi x) = \sin{(\pi x)}/(\pi x)$函數，雖然它的頻域指標最優，但是在實際情況下卻很少使用，因爲無法產生最佳的結果，無論是在采樣還是重建操作下。

從前面$sinc$函數的圖像可以看出，其能無限延伸，但是遠離中心時，函數值下降速度相對較慢 ，這是它的一個缺點；而另一個缺點是，對於一些采樣，它的負向突起也是問題。

對於高斯濾波器在面對不同類型的采樣都能得到很好的結果，即使是面對要在輸入信號中去除高頻部分的困難任務。因爲從它的傅里葉變換圖像呈現指數衰減，而且沒有會導致走樣的“突起”。對於一些不太困難的情況，tent filter就足夠了。

就重構而言，$sinc$函數的大小也會引起問題，但更重要的是，許多ripple會引起"振鈴“(ringing)現象。

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。