在第四章的4.5節已經簡單介紹過兩個shading模型，Lambertian Shading和Blinn-Phong Shading，以及Ambient Shading。本章節將進一步探討這些Shading模型以及它們的應用。

10.1 Diffuse Shading

世界上大多數物體是不光滑的(matte)，換而言之，就是從不同角度觀察物體表面上一個點，觀察到的顔色是相對穩定的。這類物體通常稱爲Lambertian objects。本節討論這類物體的shading如何實現。

注意，本章節物體坐標均為世界坐標系下；若使用透視變換後的坐標系，那麽與法綫夾角會發生變化，導致最後shading不正確

10.1.1 Lambertian Shading Model

Lambertian's cosine law：Lambertian objects均遵守該定律，該定律描述物體表面某個點的顔色c與光纖和法綫夾角成正比。

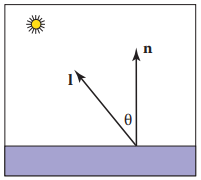
$$ \mathcal{c} \propto \cos{\theta} \\ \mathcal{c} \propto \mathbf{n} \cdot \mathbf{l} $$

注意，$\mathbf{l}$與物體的位置，這相當於假設光源位於無窮遠，投射過來的光纖被稱爲directional light，因爲只和其方向有關。

物體表面的亮暗變化與光纖的强度以及表面反射率有關。通常用$\mathcal{c}_r$表示光纖在物體表面的漫反射率(diffuse reflectance)，該反射率與顔色相關，不同顔色反射率不同。這樣，

$$ \mathcal{c} \propto \mathcal{c}_{r}(\mathbf{n}\cdot \mathbf{l}) \tag{10.1} $$

再添加光纖强度分量$\mathcal{c}_{l}$

$$ \mathcal{c} = \mathcal{c}_{r}\mathcal{c}_{l}(\mathbf{n}\cdot\mathbf{l}) \tag{10.2} $$

其中，$c_r$ 和 $c_l$ 均爲RGB的向量，取值範圍均爲[0,1]。再觀察等式(10.2)會發現，計算結果$\mathcal{c}$并不一定在[0,1]範圍内，有可能出現負值，出現負值在物理上解釋爲法綫$\mathbf{n}$和入射光綫$\mathbf{l}$在物體的兩側，如下圖所示。這種現象顯然在渲染過程中會導致錯誤，因此要對等式(10.2)進行進一步限制，有兩種處理方式。

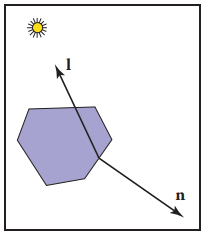
$$ \mathcal{c} = \mathcal{c}_{r}\mathcal{c}_{l}\max{(0,\mathbf{n}\cdot\mathbf{l})} \tag{10.3} $$

或

$$ \mathcal{c} = \mathcal{c}_{r}\mathcal{c}_{l}|\mathbf{n}\cdot\mathbf{l}| \tag{10.4} $$

等式(10.4)在物理含義上的解釋是非常反人類的，等式(10.4)可以想象為有兩個光源在物體的兩側，如下圖所示，因此稱爲two-sided lighting。所以，通常使用等式(10.3)作爲處理，它有良好的物理解釋以及簡潔的表示。

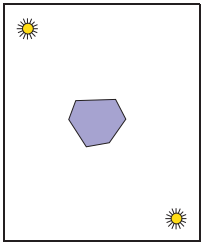
10.1.2 Ambient Shading

繼續解釋等式(10.3)，它依然包含一些缺陷，因爲，直接使用等式(10.3)時，背向光源的位置始終是黑的，這種情況和現實中顯然不匹配。因爲現實中，光纖會發生全方位反射，一些光纖會從各個方向入射背光面，因此即使處於背向光源的一側，物體表面也不可能是完全黑的。基於這個特性，通常的做法是在等式(10.3)中加入環境光項。

$$ \mathcal{c} = \mathcal{c}_{r}(\mathcal{c}_{a} + \mathcal{c}_{l}\max{(0,\mathbf{n}\cdot\mathbf{l})}) $$

為保證計算出的$\mathcal{c}$在$[0,1]^3$範圍内，那麽就需要保證$c_a + c_l \leq (1,1,1)$。否則需要對結果進行裁剪。

10.1.3 Vertex-Based Diffuse Shading

假設，使用三角形進行物體表面的近似表示，儅每個三角形只存在一個法向量進行shading，結果會呈現出多面性，爲了得到更加平滑的結果，大神們提出在三角形每個頂點都使用不同的法向量進行等式(10.3)計算，之後在使用重心插值法在三角形内部進行插值填充。如下圖所示。

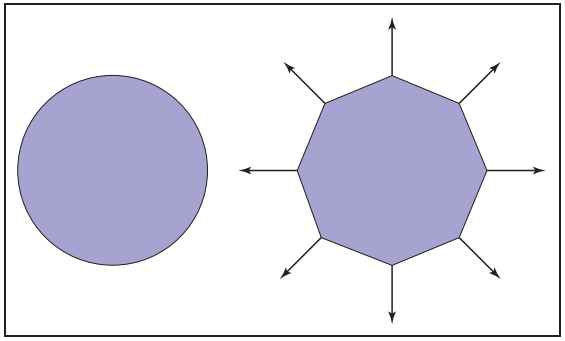
這種方法存在的一個問題是，三角形頂點的法向量怎麽獲得？如果模型有隨附法向量，那麽在細分平滑模型時，可以隨著三角形的創建而獲得。但有些多邊形模型在頂點処并沒有提供法向量，那麽可以通過平均共享該頂點的多邊形法向量來獲得。這樣獲得的法向量并不是單位向量，所以在使用前需要進行歸一化處理。

10.2 Phong Shading

一些物體表面雖然是粗糙的，但是依然會存在高光(highlight)現象，并且高光區域會隨著觀察位置的變化而變化。這就需要新增一個觀測方向$\mathbf{e}$進行分析。

再詳細描述下發生的高光現象：隨著觀察位置的變化，高光區域有時會變得模糊；高光區域反映出的顔色通常是光源顔色，物體表面顔色對其影響較小（這是因爲高光現象發生在物體表面，穿透物體表面並"拾取"物體顔色的光被散射了）。

10.2.1 Phong Lighting Model

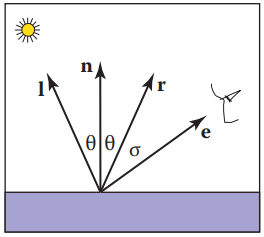
圖中，$\mathbf{l}$表示光綫方向，$\mathbf{n}$表示物體表面法綫方向，$\mathbf{r}$表示光綫在物體表面反射方向，$\mathbf{e}$表示觀測方向。其中，觀測方向與反射光綫夾角為$\sigma$。Phong Lighting模型定義高光部分是假設夾角$\sigma$越趨於零，則高光部分越亮，換而言之，觀測方向$\mathbf{e}$越接近反射光綫，高光現象越明顯，高光光斑也會從模糊變得越清晰。這個假設是符合常理的，因爲生活中，儅拿鏡子觀察某個光源時，一定是反射位置最爲晃眼。

根據這個模型假設，很容易得到： $$ \mathcal{c} = \mathcal{c}_{l}(\mathbf{e}\cdot\mathbf{r}) $$

但是，這個等式依然存在問題，第一個就是點乘$\mathbf{e}\cdot \mathbf{r}$可能存在負值；第二個更爲重要的問題就是，利用這個等式，可觀察到的高光區間會非常大，遠超出現實中的情況。基於這兩點，大神對等式做了優化： $$ \mathcal{c} = \mathcal{c}_{l}\max{(0, \mathbf{e}\cdot\mathbf{r})^p} \tag{10.5} $$

其中，$p$被稱爲Phong exponent，其值為正實數，用於控制高光區域大小。如下圖所示，不同的$p$值，有不同的高光區域。

你以爲大神對等式(10.5)的優化結束了？如果這樣就不叫大神了。

再看等式(10.5)，實際應用中，我們已知$\mathbf{l}$、$\mathbf{n}$和$\mathbf{e}$，那麽可以通過反射定律計算得到$\mathbf{r}$。

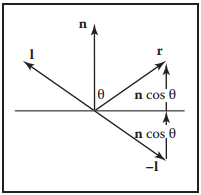
$$ \mathbf{r} = -\mathbf{l} + 2(\mathbf{l}\cdot\mathbf{n})\mathbf{n} \tag{10.6} $$

等式(10.6)看起來已經很簡單了，但是大神告訴你還不是最優的，我們計算$\mathbf{r}$是爲了得到$\mathbf{r}$和$\mathbf{e}$夾角的cosine值，它是實話只是個度量值，如果可以用其他方式得到類似的度量值，也一樣能使用。

我們知道，在反射定律中，法綫$\mathbf{n}$是入射光綫$\mathbf{l}$和反射光綫$\mathbf{r}$的角平分綫，那麽要是入射光綫$\mathbf{l}$和觀測方向$\mathbf{e}$的角平分綫$\mathbf{h}$越靠近法綫$\mathbf{n}$，是不是也能説明觀測方向$\mathbf{e}$越靠近反射光綫$\mathbf{r}$？

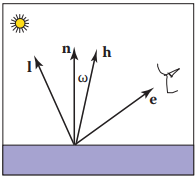
其中，$\mathbf{h}$稱爲half-vector，計算方式如下： $$ \mathbf{h} = \frac{\mathbf{e}+\mathbf{l}}{||\mathbf{e} + \mathbf{l}||} $$

這樣，等式(10.5)就可改寫爲： $$ \mathcal{c} = \mathcal{c}_{l}\max{(0,\mathbf{h} \cdot \mathbf{n})}^p \tag{10.7} $$

等式(10.7)的優勢在於足夠簡單，雖然細節上，使用$\mathbf{h}$和$\mathbf{n}$來代替$\mathbf{e}$和$\mathbf{r}$會有一些區別，但是并不影響結果。它的缺點在於存在平方根和除法運算。

有了高光項，結合等式(10.3)和等式(10.7)可得：

$$ \mathcal{c} = \mathcal{c}_{r}(\mathcal{c}_{a} + \mathcal{c}_{l}\max{(0,\mathbf{n}\cdot\mathbf{l})}) + \mathcal{c}_{l}\max{(0,\mathbf{h}\cdot\mathbf{n})^p} \tag{10.8} $$

如果允許調整高光項的亮度和顔色，可以加入控制項$\mathcal{c}_{p}$。

$$ \mathcal{c} = \mathcal{c}_{r}(\mathcal{c}_{a} + \mathcal{c}_{l}\max{(0,\mathbf{n}\cdot\mathbf{l})}) + \mathcal{c}_{l}\mathcal{c}_{p}\max{(0,\mathbf{h}\cdot\mathbf{n})^p} \tag{10.9} $$
注意，以上所有向量閒的運算都需要轉換爲單位向量！

10.2.2 Surface Normal Vector Interpolation

和具有相同幾何形狀的Lambertian表面相比，具有高光的光滑表面往往會快速改變顔色。因此，只在具有法向量的位置進行shading，會產生僞影現象。爲了減少這種現象，可以在多邊形内部插值出每個位置的法向量，然後使用上面提到的Phong模型進行shading操作。插值法向量的方法和在三角形内部插值顔色類似。

$$ \mathcal{c} = \alpha\mathcal{c}_0 + \beta\mathcal{c}_1 + \gamma\mathcal{c}_2 \tag{10.10} $$
$$ \mathbf{n} = \alpha\mathbf{n}_0 + \beta\mathbf{n}_1 + \gamma \mathbf{n}_{2} \tag{10.11} $$

由等式(10.11)得到的法向量，需要經過歸一化處理才能在shading過程中使用。這種法向量的插值方式通常也稱爲Phong normal interpolation。

10.3 Artistic Shading

前面介紹的兩種shading模型都是仿真物體在真實環境中的表現。而Artistic shading則是模仿人類藝術家的繪畫，這種方式通常稱爲non-photorealistic rendering。

10.3.1 Line Drawing

轮廓，silhouettes，现实中物体不会出现，只有人们在绘图时才会出现的。假设两个三角形有一条共边，当其中一个三角形与观察方向同侧，而另一个三角形在异侧时，此時就需要繪製出三角形邊緣作爲輪廓。這種情況可用如下形式判斷是否需要繪製輪廓。 $$ (\mathbf{e}\cdot\mathbf{n}_0)(\mathbf{e}\cdot\mathbf{n}_1) \leq 0 $$

其中，$\mathbf{e}$表示邊緣與觀察者的連綫方向。這可推廣到兩個三角形所在的平面，假設平面方程為$f_i(\mathbf{p}) = 0$，那麽： $$ \text{draw silhouette if } f_0(\mathbf{e})f_1(\mathbf{e}) \leq 0 $$

另外，現實中，儅用多邊形表示平滑表面時，并不會將每個多邊形的可見邊界都繪製出來，而是在真正有摺痕或轉角的地方才繪製，因此可以設定一個閾值用於判斷： $$ \text{draw crease if }(\mathbf{n}_0 \cdot \mathbf{n}_1) \leq threshold $$

結合繪製摺痕和繪製輪廓，可以得到非常漂亮的line drawing圖。

10.3.2 Cool-to-Warm Shading

藝術家在對綫圖進行shading操作時，通常會采用低强度的陰影來展示曲面的效果，并對物體進行上色。(還是看原文吧，When artists shade line drawings, they often use low intensity shading to give some impression of curve to the surface and to give colors to objects)。上色時，其中面向一個方向的會使用冷色調，另一個方向會使用暖色調。這些顔色的使用不會非常飽和，也不會非常暗，這樣就使得黑色輪廓有非常好的展示效果，cartoon-like effect。

根據上面的描述，可以假設一個"暖"色光綫$\mathbf{l}$，以及"暖度"$k_w$，“暖度”的計算依然與光綫和法綫夾角有關，取值範圍為$[0,1]$。 $$ k_w = \frac{1+\mathbf{n}\cdot\mathbf{l}}{2} $$

這樣著色點的顔色可以利用"暖度"來計算。 $$ \mathcal{c} = k_wc_w + (1 - k_w)c_c. $$

其中，$c_w$和$c_c$分別表示暖色調顔色和冷色調顔色。例如，

$$ c_c = (0.4,0.4,0.7),\\ c_w = (0.8,0.6,0.6) $$

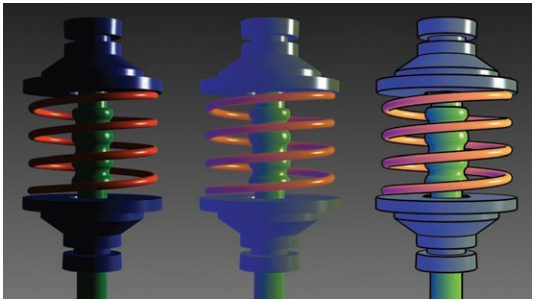
下圖展示了傳統的Phong lighting和上面提到的shading方式。

Frequently Asked Questions

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。