何爲紋理？在圖形學中，定義物體表面空間變化屬性，即隨著空間位置變換，物體表面呈現出不同屬性，但這種屬性并未真的改變整個物體表面形狀，我們將這種變換的屬性稱爲物體表面紋理。

圖形學中，爲了在物體表面獲得紋理效果，會使用紋理映射(texture mapping)技術：該技術使用一幅圖像，稱爲紋理圖（texture map、texture image或texture），該圖像包含所有物體表面紋理信息，然後通過數學上的映射，將該圖像“放置”到物體表面。

本章討論紋理表示物體表面細節、陰影和反射。基本思想比較簡單，但是在實際應用中會遇到一些問題。第一，紋理圖通常需要扭曲使用，因此設計紋理圖到物體表面的函數映射關係是一個巨大的挑戰；第二，紋理映射是一個重采樣過程，重采樣就容易出現走樣現象，許多紋理映射器的複雜度高就是爲了解決這些走樣失真導致的。

11.1 Looking Up Texture Values

回顧第十章中Lambertian shading model的公式： $$ \mathcal{c} \propto \mathcal{c}_{r}(\mathbf{n}\cdot \mathbf{l}) $$

$\mathcal{c}_r$表示光纖在物體表面的漫反射率(diffuse reflectance)，通常用RGB表示，假如將該值替換成紋理圖上某個點坐標係下RGB取值，這樣就能將紋理圖順利映射到物體表面。那麽，應該取紋理圖上哪個點的RGB值呢?

獲取紋理圖中某個點位置取值叫做texture lookup：它在紋理圖中找到與著色點相對應的位置，並讀取該位置紋理信息，從而生產紋理樣本。實現代碼如下：

從上面代碼中可以看出，紋理映射的一個關鍵要素是設計一個從物體表面到紋理圖上的映射函數（texture coordinate function)。如下圖所示：

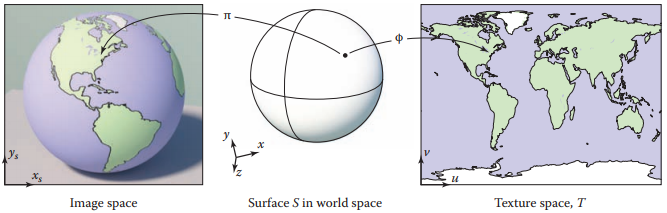
上圖中，假設空間坐標系中物體表面為$\mathcal{S}$，紋理空間為$\mathcal{T}$，則映射函數$\Phi$表示爲： $$ \phi: \mathcal{S} \rightarrow \mathcal{T} : (x,y,z) \mapsto (u,v) $$

通常，紋理空間$\mathcal{T}$爲一幅圖像，定義在單位正方形中：$(u,v) \in [0,1]^2$。另外在本章中，定義$\pi$為視圖變換（從空間中映射到圖像空間）。相比$\pi$和$\phi$兩種映射，$\pi$通常只有一種形式，要麽是透視投影，要麽是正交投影，而$\phi$則有多種形式（相當於分段函數）。

紋理映射的另一個問題是，儅以大傾斜角將高分辨率紋理映射到低分辨率圖像上時，就會發生常見的走樣現象，如下圖所示。圖中遠處直綫明顯存在斷裂，這就是由走樣現象引起的。

至此，可以知道，紋理映射要解決的兩個主要問題：

  • 定義坐標映射函數；
  • 在不引入走樣的情況下，查詢紋理值。

11.2 Texture Coordinate Functions

紋理坐標映射函數$\phi$非常重要，而且它并非圖形學中的新問題。在早期製圖傢繪製地圖時，從地球儀映射到地圖上，不可避免地會導致面積、角度或距離的變形，而引起地圖偏差。因此，幾個世紀以來，許多地圖映射方式被提出，都爲了平衡紋理映射中在一個連續區域最小化變形的同時能夠覆蓋更大的面積， 這個相互矛盾的問題。

在設計紋理坐標映射函數$\phi$時，有一些挑戰性的目標需要考慮：

  • 雙射性（Bijectivity）：我們希望函數$\phi$能保證表面上的一個點只與紋理上的一個點對應，反之也要成立，除非紋理圖像在物體表面是重複出現的，否則意外出現一對多的情況將引起“災難”；
  • 尺寸失真（Size distortion）：物體表面上的紋理比例要保持恆定，換句話說，就是物體表面距離相近的兩個點，應該映射到紋理空間中距離相近的兩個點；從數學角度解釋就是，函數$\phi$的導數值不能太大。
  • 形狀失真（Shape distortion）：紋理不能嚴重失真，例如物體表面上一個非常小的圓，映射到紋理空間后因大致保持圓形，而不能出現被嚴重擠壓或拉伸的形狀。換而言之，函數$\phi$各個方向上導數不能有太大差異。
  • 連續性（Continuity）：保證物體表面上相鄰的點，映射后也是相鄰的。這就要保證函數$\phi$的連續性，讓它不連續點盡可能少。若一些情況下，不連續不可避免，那麽最好將這些不連續的點放到不引人注意的地方。

定義物體表面有兩種方式：一種是通過參數表示法，一種是通過三角形mesh結構描述；這兩種方法經過不同的處理，都能得到紋理坐標的映射關係。廣義的說，這兩種方法都是從幾何角度計算紋理坐標。

11.2.1 Geometrically Determined Coordinates

下面來説明各種映射方法，以下圖爲例，圖中數字相當於坐標$(u,v)$，網格綫是爲了觀察映射后的失真。

figure11.4

平面投影 - Planar Projection

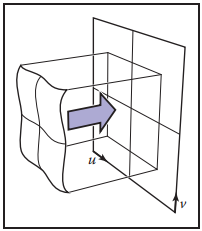
平面投影類似第七章中的正交投影；正交投影通過乘以一個矩陣並忽略$z$分量實現，這裏的平面投影也類似： $$ \phi(x,y,z) = (u,v),\ \begin{bmatrix} u\\ v\\ \star\\ 1 \end{bmatrix} = M_t\begin{bmatrix} x\\ y\\ z\\ 1\end{bmatrix} $$

其中$M_t$表示紋理仿射變換矩陣，$\star$表示我們并不在意該位置取值。這種方式的投影，在平坦的表面效果非常理想，但是，儅物體是“封閉”時，這種投影方式將不再是單射。例如下圖。

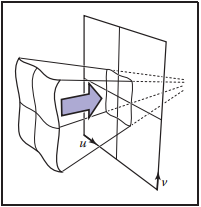
儅用透視變換的方式來做修改，可以得到類似的變換結果：

$$ \phi(x,y,z) = (\tilde{u}/w, \tilde{v}/w), \ \begin{bmatrix} \tilde{u}\\ \tilde{v}\\ \star \\ w \end{bmatrix} = P_t \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} $$

結果如下圖所示：

Spherical Coordinates

對於球體，經緯度的參數表示是廣汎應用的，同樣在球體兩極存在變形也是衆所周知的。

儅紋理利用球體存放，對類球物體表面進行紋理映射時，可以采用徑向投影(radial projection)；換種説法，假設類球表面坐標為$(\rho, \theta, \phi)$，忽略$\rho$，將$\theta$和$\phi$分別映射到區間$[0,1]$上即可。即利用球體坐標轉換可得： $$ \phi(x,y,z) = ([\pi + atan2{(y,x)}]/2\pi, [\pi - acos(z/\sqrt{x^2+y^2+z^2})]/\pi) $$

如果從中心點可以看到整個表面，那麽除去兩極，其他位置均爲"雙射”；下圖就是采用這種方式對類球物體進行紋理映射的結果。

Cylindrical Coordinates

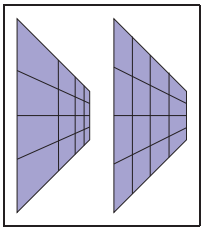
假設物體形狀類似柱形，那麽使用柱坐標要比球坐標來的合適。如下圖所示，下圖中左圖為利用球坐標進行映射的結果，右圖為利用柱坐標進行映射的結果。

與球坐標類似，柱坐標可以按如下方式計算： $$ \phi(x,y,z) = (\frac{1}{2\pi}[\pi + atan2(y,x)]/2\pi, \frac{1}{2}[1+z]) $$

Cubemaps

利用球坐標對球體或類球體進行映射，在兩極出會存在面積和形狀的高度失真，爲了解決這個問題，一種做法是通過犧牲連續性來實現。就是將球體改爲立方體，將紋理存放在立方體上，這種用六個面存放紋理就稱爲cubemap。這種方式在立方體的邊上不連續，但它能夠降低形狀和面積的失真。

相比于球坐標和柱坐標，cubemaps的紋理坐標計算效率要高得多，因爲映射到平面上只需要一個除法就行。例如，立方體$+z$面的映射結果： $$ (x,y,z) \mapsto (\frac{x}{z}, \frac{y}{z}) $$

如何生成cubemaps假設，一個紋理已經存放在球體上，那麽將一個立方體(cube)將該球體包圍在中間，之後從球心出發，與球體表面每個點連綫並延長，最終會和立方體表面相加，將球體上的點映射到立方體表面交點即可。如下圖所示。

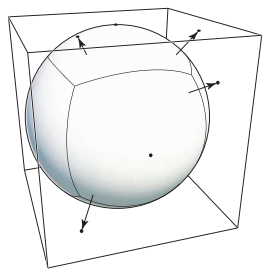
cubemaps一个非常恶心的问题就是，六个面的$(u,v)$的方向如何定义；理論上任何方式都行，但不同的定義會導致最終結果不同。對於OpenGL，其定義如下：

$$ \begin{align} \phi_{-x}(x,y,z) &= \frac{1}{2}[1 + (+z, -y)/|x|],\\ \phi_{+x}(x,y,z) &= \frac{1}{2}[1 + (-z, -y)/|x|],\\ \phi_{-y}(x,y,z) &= \frac{1}{2}[1 + (+x, -z)/|y|],\\ \phi_{+y}(x,y,z) &= \frac{1}{2}[1 + (+x, +z)/|y|],\\ \phi_{-z}(x,y,z) &= \frac{1}{2}[1 + (-x, -y)/|z|],\\ \phi_{+z}(x,y,z) &= \frac{1}{2}[1 + (+x, -y)/|z|] \end{align} $$

這裏如果結合書本中的圖來理解是錯誤的；

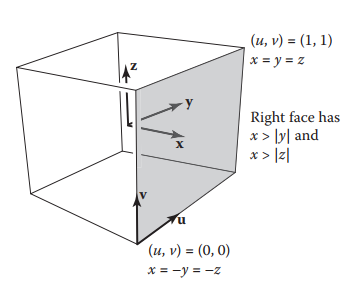
因爲書本中的圖和OpenGL的定義無法對照上。下面給出理解OpenGL的圖。

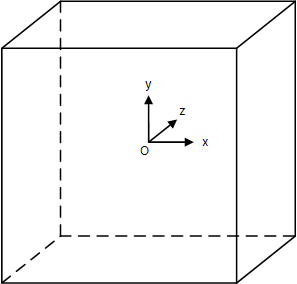
OpenGL定義，$+x$為右面，$-x$為左面，$+y$為上面，$-y$為下面，$+z$為背面，$-z$為正面；那麽$(u,v)$的方向為：從原點$O$（位於立方體内部）出發，沿著觀測方向所得的立方體表面的右下角為紋理坐標系原點，$u$軸始終位於$v$軸的逆時針方向上。例如，立方體的右面，其原點位置如下圖所示。

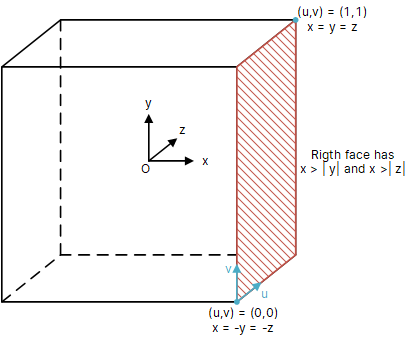
用戶判斷紋理坐標映射到立方體哪個面上，可以通過以下方式進行：原始坐標$(x,y,z)$中，絕對值最大的為觀測方向，例如，$|x| > |y|$并且$|x| > |z|$，那麽最終紋理會在$+x$或$-x$面上，取決於$x$的符號。

下面給出OpenGL下各個面的紋理坐標原點位置。

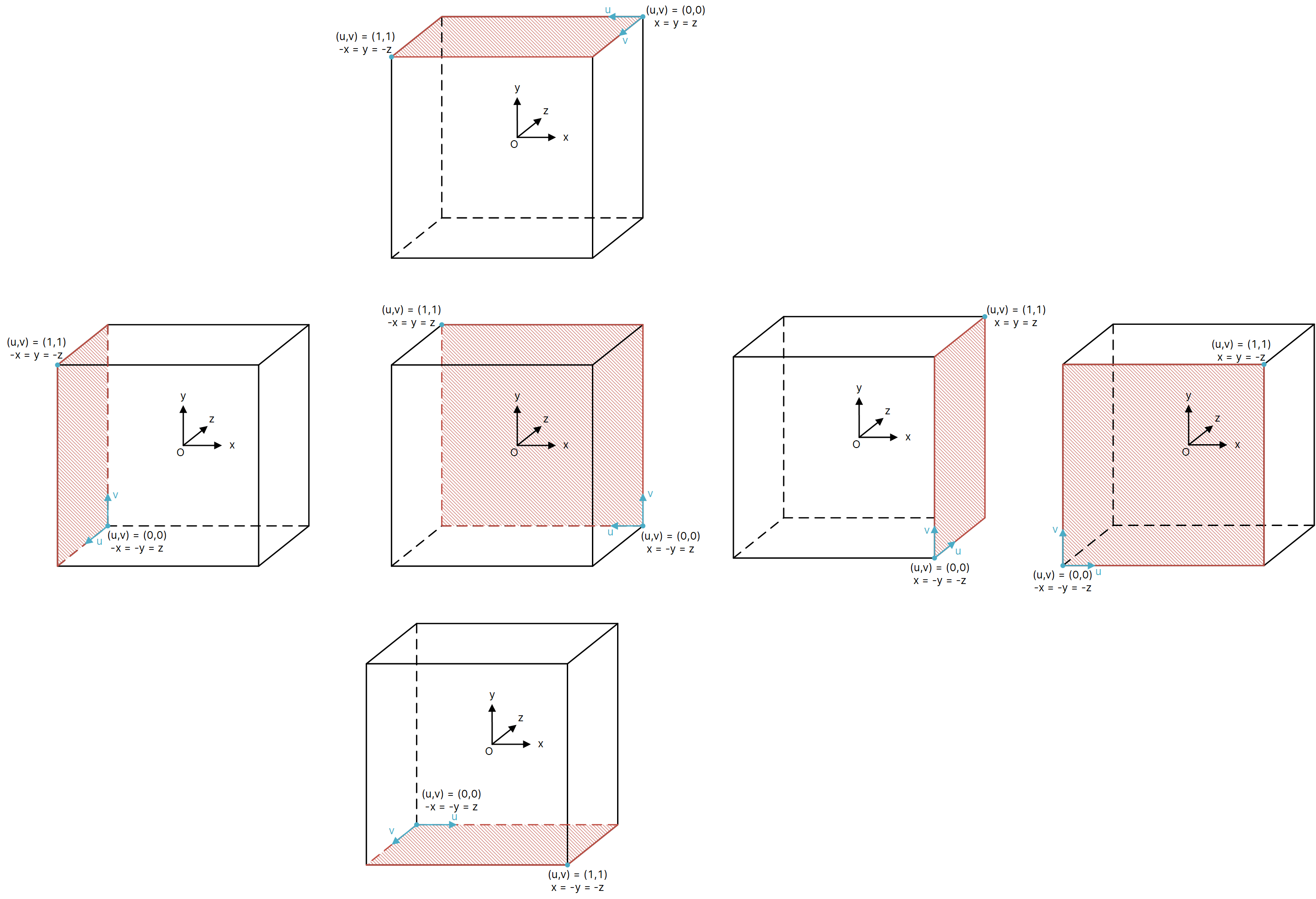
OpenGL那部分屬於個人理解，不知道是否有理解錯誤，歡迎指正。

11.2.2 Interpolated Texture Coordinates

對於一些需要精細控制的表面，通常會使用mesh的方式表示，這樣就能顯示存儲頂點對應的紋理坐標，之後通過重心插值法完成整個mesh的映射。例如下圖。

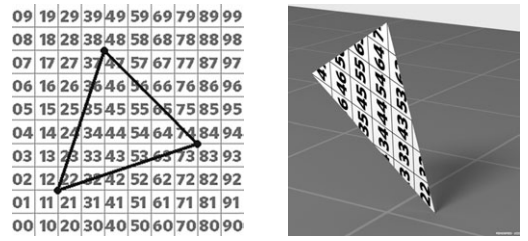
下圖展示了完整的mesh的紋理貼圖。

可以看出，利用圖11.4的貼圖進行紋理映射，可以可視化結果，方便的調試紋理映射代碼。值得注意的是，這種方式的映射質量很大程度上與mesh在紋理空間中的分佈有關。但是無論如何分佈，只要保證mesh共享頂點，那麽紋理坐標映射就始終是連續的。

對於尺寸失真，儅紋理空間中的網格面積與物體空間中的面積成比例時，尺寸失真較低。

對於形狀失真也與尺寸失真類似。上圖中，對於臉部的紋理映射失真較小，但是對於地球儀的紋理貼圖中，在兩極位置的形狀失真就非常明顯。

11.2.3 Tiling, Wrapping Modes, and Texture Transformation

這裏還要解決一個細節問題：由於“四捨五入”的誤差，紋理坐標有可能超出紋理圖的邊界，此時如何處理？

假設紋理只是映射到物體表面的一小部分區域，但是紋理坐標變換關係是紋理圖與整個表面。一種方式是：所使用的紋理圖應該是大部分是空白的，需映射的部分在整張紋理圖中也只有一小部分。這個方法會導致紋理圖的分辨率非常高（這樣有效區域細節才能保留）。另一種方法是：對所有紋理坐標進行等比例縮放，以使其覆蓋更大的範圍。

儅紋理坐標超過單位區域時，如何取值？一種方式是，事先設定好背景值，儅越界時都用背景值填充。另一種方式是截斷超出範圍，使用邊界值填充。

還有一種情況是，當我們希望重複我們的紋理圖時，例如棋盤格，構建一張完整的紋理是非常浪費資源的。我們可以只構建最小紋理圖，然後使用“坐標環繞”的方式讓紋理圖不停的重複。例如，查詢到的紋理坐標在右邊越界了，那麽就從紋理圖的左邊界開始重新搜索越界部分。這樣使用最簡單的除餘運算就能實現。兩種方式的代碼如下所示，上面的為“坐標環繞”的方式，下面為截斷方式。

儅需要調整紋理的比例或位置時，并不需要改變紋理函數，或者改變mesh中的頂點坐標，只需要利用一個變換矩陣$M_T$對原來的紋理坐標進行變換即可。 $$ \phi(x) = M_T\phi_{model}(x) $$

其中，$\phi_{model}$是模型提供的紋理坐標函數，$M_T$是一個$3\times 3$的仿射或投影變換矩陣。

11.2.4 Perspective Correct Interpolation

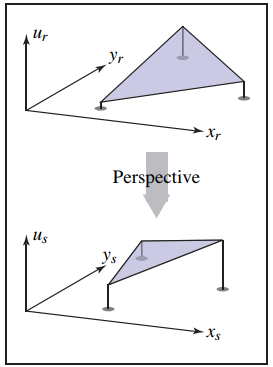
本節説明透視過程中的插值問題。先觀察下圖。

上圖中，左側為正確的透視結果，而右側是在圖像空間中的插值結果。直覺上，我們會使用如下方式計算透視圖。

這種方式就會導致上面右側圖像的錯誤。那原因是什麽呢？觀察從世界坐標系$\mathbf{q}$到齊次點$\mathbf{r}$，再到齊次化的點$\mathbf{s}$：

$$ \begin{bmatrix} x_q\\ y_q\\ z_q\\ 1 \end{bmatrix} \underrightarrow{transform} \begin{bmatrix} x_r\\ y_r\\ z_r\\ w_r\end{bmatrix} \underrightarrow{homogenize}\begin{bmatrix} x_r/w_r\\ y_r/w_r\\ z_r/w_r\\ 1\end{bmatrix} \equiv \begin{bmatrix} x_s\\ y_s\\ z_s\\ 1 \end{bmatrix} $$

上面代碼中的插值發生在點$\mathbf{s}$処，也就是齊次化后，可真實的插值應該發生在空間$\mathbf{q}$或$\mathbf{r}$中，因爲這個空間中，此時齊次除法還沒有對三角形重心坐標進行非綫性變換。

用個例子解釋，假設空間中有$\mathbf{q}$和$\mathbf{Q}$兩點連成的一條直綫，$\mathbf{q’}$在直綫$\mathbf{qQ}$上。可表示爲 $$ q’ = \mathbf{q} + \alpha(\mathbf{Q} -\mathbf{q}) $$

而點$\mathbf{q}$和點$\mathbf{Q}$映射到紋理空間中為點$\mathbf{s}$和點$\mathbf{S}$，直綫$\mathbf{qQ}$上的點$\mathbf{q’}$映射為點$\mathbf{s’}$，可表示為 $$ s’ = \mathbf{s} + t(\mathbf{S} - \mathbf{s}) $$

根據透視變換的性質，比例值$\alpha$和$t$顯然是不相等的，但他們之間的關係如下 $$ t(\alpha) = \frac{w_r \alpha}{w_R + \alpha(w_r - w_R)} \ \text{and}\ \alpha(t) = \frac{w_R t}{w_r + t(w_R-w_r)} \tag{11.1} $$

等式(11.1)提供了一種修正方式，$u_s’ = u_s + t(\alpha)(u_S - u_s)$和$v_s’ = v_s + t(\alpha)(v_S - v_s)$。修正結果如下。

但是對每個fragment都進行修正效率太低，下面介紹一種更簡單的方式。先回顧下透視變換的特點，透視變換后依然會保持物體的直綫性和平面性，這個特點保證了我們使用綫性插值是可行的。儘管透視變換保持了直綫性和平面性，但是，在直綫或平面内部是發生變形，所以導致紋理映射結果出錯。由於紋理坐標$(u,v)$是關於空間位置$(x_q, y_q, z_q)$的函數，那麽在空間點$(x_q,y_q,z_q)$變換到齊次坐標$(x_r,y_r,z_r,w_r)$過程中，紋理查詢位置是不會發生變化的，將紋理坐標加入後面的齊次除法運算，可以讓非綫性變換造成的影響同樣作用到紋理坐標上，而不導致映射過程出現偏差。

$$ \begin{bmatrix} u\\ v\\ 1\\ x_r\\ y_r\\ z_r\\ w_r \end{bmatrix} \underrightarrow{homogenize}\begin{bmatrix} u/w_r\\ v/w_r\\ 1/w_r\\ x_r/w_r\\ y_r/w_r\\ z_r/w_r\\ 1 \end{bmatrix} \tag{11.2} $$

現在，假設要對一個三角形區域内的紋理坐標進行插值，按照前面光柵化代碼中的方式獲得的紋理坐標只是等式(11.2)中的$(u/w_r, v/w_r)$，爲了校正結果我們需要得到$1/w_r$，這同樣可以通過插值方式計算得到，可以證明出插值方式得到的$1/w_r$與下面方式得到的結果一致： $$ \frac{1}{w_r} + \alpha(t)\left(\frac{1}{w_R} - \frac{1}{w_r}\right) = \frac{1}{w_r’} = \frac{1}{w_r + t(w_R - w_r)} \tag{11.3} $$

這樣，光柵化階段的代碼可修改為下面形式：

11.2.5 Continuity and Seams

紋理映射函數除了低失真的要求，還有連續性的要求，通常在實際使用過程中，不連續的情況無法消除。不連續的地方通常會有“縫合”的痕跡，例如前面介紹的cubemaps的棱邊。所以在進行插值紋理坐標時需要對不連續的地方單獨考慮，如果依然使用連續性的插值，那麽會出現下面這種高度失真，因爲這樣就不是單射了。

避免這一現象的方法是在“縫合”処避免共享紋理坐標。例如上圖中的右圖。

11.3 Antialiasing Texture Lookups

反走樣是紋理坐標查找的第二個基本問題。紋理坐標映射過程相當於一個采樣，只要是采樣就會遇到走樣的問題。紋理的走樣問題主要體現在兩種情況下：第一，將分辨率高的紋理圖貼到分辨率低的物體表面，這種情況通常采用區域平均值替代單個點像素值；第二種情況是將低分辨率紋理圖貼到高分辨率物體表面，采用第九章中提到的重建濾波器進行插值。這兩種情況會在之後詳細説明。

11.3.1 The Footprint of a Pixel

先看下圖

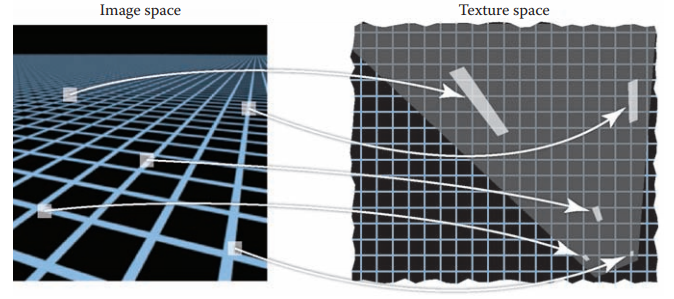
從圖中可以發現，在圖像空間中，不同位置、相同大小的區域映射到紋理空間中所占的區域大小、形狀是不同的。我們將其在紋理圖中所占區域稱爲texture space footprint。若在映射過程中，依然采用Nearest-Neighbor方式取值，就會引起走樣現象。如果將所占區域像素平均值來替代Nearest-Neighbor取值，能夠降低走樣現象。那麽如何查詢區域像素平均值呢？

回顧三維空間中，物體通過$\pi$映射到圖像空間，通過$\phi$映射到紋理空間，那麽從圖像空間到紋理空間可以通過$\Phi = \phi \circ \pi^{-1}$進行；因此，圖像空間像素的footprint可以通過$\Phi$計算得到。可以看出，像素的footprint與兩個因素有關，一個是viewing，一個是紋理坐標映射函數。例如，儅物體離相機近時，footprints所占區域小，遠離相機時，footprints所占區域大。爲了快速有效的查詢區域像素平均值，我們通常會使用大量的近似，綫性近似就是一個不錯的選擇。 $$ \Phi(\mathbf{x}) = \Phi(\mathbf{x}_0) + \mathbf{J}(\mathbf{x}-\mathbf{x}_0) $$

其中 ，$\mathbf{J}$為$2 \times 2$矩陣，是對$\Phi$的導數的近似表示。如果圖像空間中的點表示爲$\mathbf{x} = (x, y)$，紋理空間中的點表示爲$\mathbf{u} = (u, v)$，那麽：

$$ \mathbf{M} = \begin{bmatrix} \frac{du}{dx} & \frac{du}{dy}\\ \frac{dv}{dx} & \frac{dv}{dy} \end{bmatrix} $$

該矩陣描述了在點$(x,y)$上，紋理坐標$(u,v)$隨著$(x,y)$變化的彎曲趨勢和程度。這種近似方式的幾何解釋為：圖像空間中，以$\mathbf{x}$為中心的單位面積區域，映射到紋理空間后，類似以$\Phi(\mathbf{x})$爲中心的平行四邊形區域，它的邊平行於向量$\mathbf{u}_x = (du/dx, dv/dx)$和$\mathbf{u}_y = (du/dy, dv/dy)$。例如下圖所示。

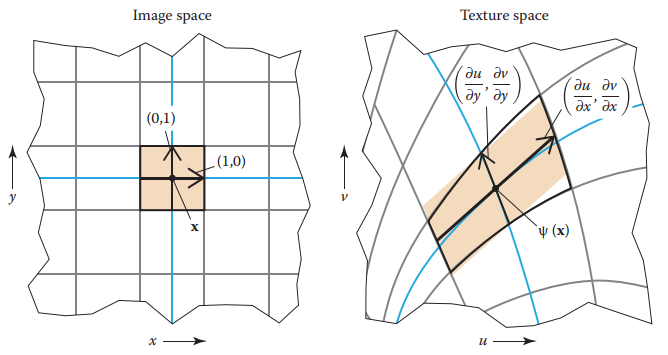
接下去的問題是如何計算所占平行四邊形的區域平均值？通常平行四邊形面積平均值計算是開銷巨大的，所以采用了近似的方式獲得。

11.3.2 Reconstruction

對於分辨率不同的圖像和紋理圖，它們之間的映射就是信號重建的過程，那麽必然用到重構濾波器。先看下圖。

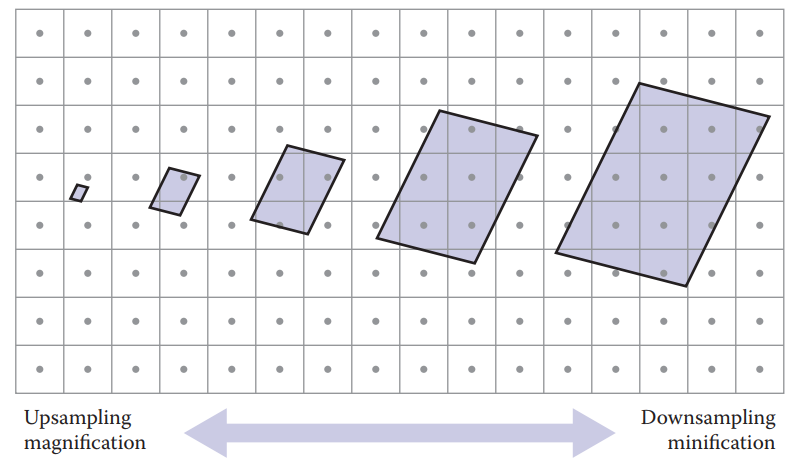
從圖中可以看出，對於上采樣(upsampling)，圖像空間内一個像素點映射到紋理空間所占區域較小，此時通過插值來避免塊狀失真；而對於下采樣(downsampling)，圖像空間内一個像素點映射到紋理空間所占區域較大，如何有效計算所覆蓋區域的平均值就是其所面臨的挑戰。

本節先解釋上采樣過程，在第九章提到過，采用高質量的濾波器其計算開銷也是巨大的，所以通常采用雙綫性插值(bilinear-interpolation)的方式。代碼如下。

但是，雙綫性插值的方法依然有瓶頸，因爲它需要獲得附近位置的四個像素點，這就會導致内存讀取的延遲而降低效率，所以爲了高效，通常會硬件化這個操作。

11.3.3 Mipmapping

前面説了要計算四邊形内像素點的平均值，直覺的做法會是：判斷點是否在四邊形内，然後把在四邊形内的所有點都加起來求平均。這種做法計算開銷非常大，而本節介紹一種可以事先計算好區域面積，之後只需要查詢就行的方式——“MIP mapping”。

mipmap是一系列分辨率越來越低的紋理圖，如下圖所示，原始紋理圖記爲Level-0層，每降采樣一次，層數加$1$，記爲Level-D，直到只剩一個像素爲止。降采樣過程利用$2 \times 2$的核對上一層進行average-pooling計算，這樣就得到長寬各減半的圖像，利用公式$log_2 N$就可知道能生成幾層圖像序列。

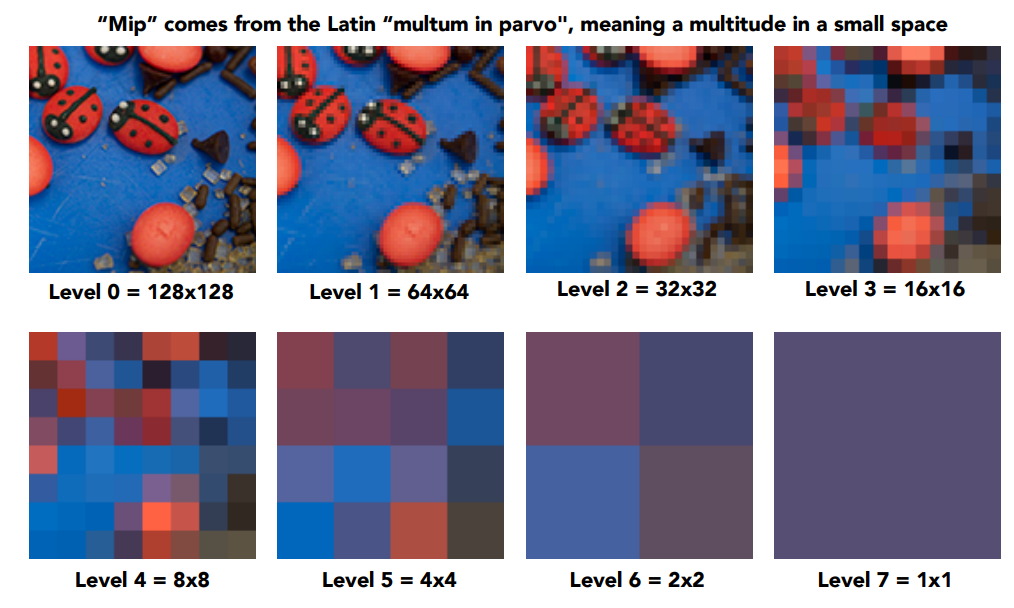
mipmap的層級關係如下。

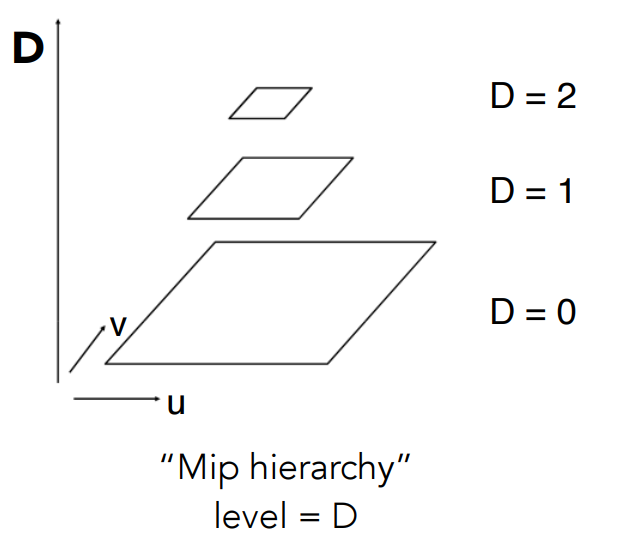
由於降采樣過程是長寬減半，通常mipmap要求查詢區域和紋理圖像是正方形，且邊長為$2^k$個像素。我們把mipmap生成的一系列圖像也稱爲圖像金字塔(image pyramid)。使用mipmap就是典型的空間換時間，而它所增加的空間也只是原始圖像的$\frac{1}{3}$。

11.3.4 Basic Texture Filtering with Mipmaps

有了圖像金字塔，我們可以在常數時間内查詢到每個像素覆蓋紋理面積的平均值。由於mipmap只能查詢正方形區域，所以同樣會引入失真；但暫且抛開查詢形狀與真實形狀不一致的問題，看看正方形區域如何查詢。

假設，待查詢正方形邊長為$D$，該長度是Level-0層（即原始紋理圖）下尺寸；由於mipmap是按$2$的倍數降采樣，所以可以按下面等式對邊長進行近似： $$ 2^k \approx D \rightarrow k = log_2D $$

由於$k$值多數情況是非整數，我們有兩種辦法來進行近似；第一種，用最近鄰法，取離$k$值最近的整數層進行查詢；第二種，利用綫性插值，將離$k$值最近的兩層取出，分別在這兩層内做綫性插值，之後再在兩層閒做綫性插值。

有了查詢方法，那麽$D$值如何確定？特別是在所占區域非正方形的情況下。我們可以利用面積的平方根或計算所占區域的長軸作爲寬度，但是爲了效率，通常使用下面方式獲得： $$ D = \max{({||u_x||, ||u_y||})} $$

這樣，整個mipmap查詢框架就能構建出來了。

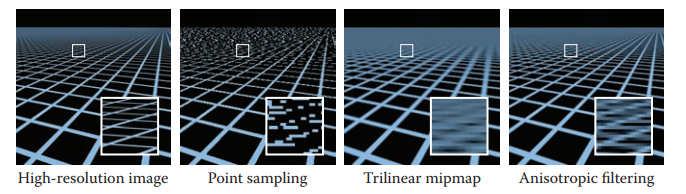
雖然mipmap對於反走樣有很好的效果，但是其不具備各向異性(anisotropic)的能力導致在觀察傾角很大時，效果并不理想。所以，又引入了Anisotropic Filter。先對比這幾種方式獲得的圖像效果。

11.3.5 Anisotropic Filter

在mipmap中，我們利用長軸作爲寬度$D$計算$k$值，如果改用短軸作爲寬度$D$，然後沿著長軸進行多次查詢，將這些結果再做平均也能得到很好的效果，這種方式就是Anisotropic Filter的一個體現。

當然還有其他方式，在Games101課程中，閆老師提到了Ripmaps各向異性操作。其生成的圖像序列如下，圖片來自維基百科。

可以看出，mipmaps只是記錄了對角綫上的圖像序列，所以它只能查詢正方形區域，而ripmaps記錄了長寬方向上所有變化的圖像序列，所以對各向異性區域有很好的近似。但是，也僅是對與軸平行的區域效果較好，而對對角區域依然會引入是真。另外，ripmaps的存儲空閒比原來增加了3倍。

課程中還提到了EWA filter，它能處理任意區域，它引入了權值，並進行多次查詢獲得結果，細節請自行google。

11.4 Applications of Texture Mapping

紋理映射是一個與應用緊密相關的工具，本節介紹幾種紋理映射的重要應用。

11.4.1 Controlling Shading Parameters

紋理映射最基本的用法就是通過著色計算中使用漫反射顔色來引入顔色變化。但是，并沒有規定只能對顔色進行變化，同樣可以對物體的其他屬性進行變化，例如鏡面反射率、鏡面粗糙度等。擧個例子，例如硬紙板做成的紙盒，其顔色是均匀的，但是如果有膠帶的地方，會使鏡面反射率提高，而粗糙度降低。

使用不同參數進行映射時，需要注意這些參數閒的關係：例如下圖中的光滑陶瓷杯子，在其映有圖案的地方會同時改變其粗糙度和亮度。

11.4.2 Normal Maps and Bump Maps - 法綫貼圖和凹凸貼圖

在著色過程中，另一個關鍵量是物體表面法綫。在第八章中介紹過可以通過插值方式獲得頂點外其他位置的法綫，但是，有時候物體表面并非平整的，所以法綫方向與基礎表面法綫方向并不相同。所以，法綫貼圖就能通過查詢紋理圖獲得每個位置的法綫信息。

要注意的是，法綫貼圖中，法綫信息通常是在物體空間下的，我們需要將其轉換到世界空間中才能用於後續光照的計算。就因爲法綫是在物體空間下，所以其是與物體表面相關的，若物體表面發生變化，法綫貼圖中的法綫也要跟隨變化，否則無法使用法綫貼圖。為解決這個問題，可以為法綫定義一個與物體表面相關的坐標系，例如，基於物體表面的切平面空間，紋理坐標函數本身就提供了一對切向量，一般情況下，這一對切向量并不正交，可以使用第二章中介紹的方法對它們進行正交化后使用。

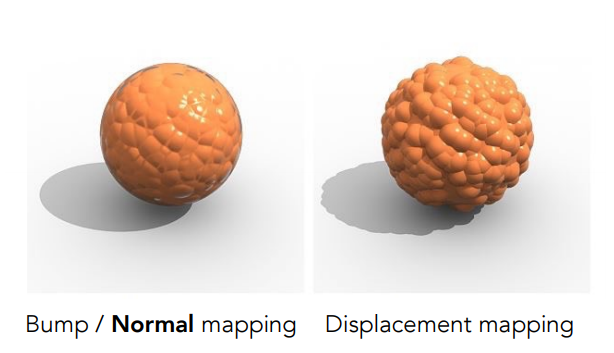
如何獲得法綫貼圖？一種是通過模型計算得到；一種是通過直接測量真實表面獲得。當然還有另一種方法，在建模過程中獲得：這時候通常使用凹凸貼圖來間接指定法綫。凹凸貼圖的核心思想就是高度場變化：通過一個函數定義物體表面局部區域的高度變化。下圖展示凹凸貼圖的效果提升。

從凹凸貼圖中推導法綫貼圖是非常簡單的。該章節沒説怎麽做，但在作者的第二版書中凹凸貼圖部分有提到，其實際是對物體表面法綫進行擾動，而凹凸貼圖記錄的就是擾動量，只需將這個擾動量直接叠加到物體表面法綫上即可。

11.4.3 Displacement Maps - 位移貼圖

上面提到的法綫貼圖，本質上并未改變物體的表面，只是在視覺上進行了trick。而位移貼圖則會真正的改變物體表面形狀：位移貼圖的紋理信息記錄尺度信息——偏離“基準面"的高度。根據這個信息，將每個著色點沿著法綫方向移動到新位置，法綫方向可能大致相同，但是物體表面已經發生變化。

下圖是凹凸貼圖和位移貼圖的效果對比。

11.4.4 Shadow Maps - 陰影貼圖

陰影是展示場景中物體關係的一個重要手段。下圖展示了有無陰影的效果對比。

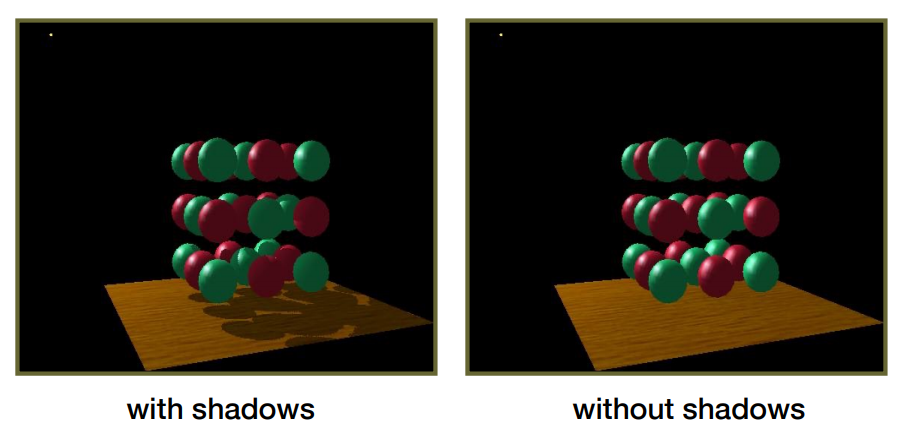
陰影貼圖利用紋理映射技術實現點光源產生的陰影效果。想象一個點光源向有限方向範圍内發出光。被照亮的物體是將光源連接離它最近物體表面點的綫段的并集。如下圖所示。

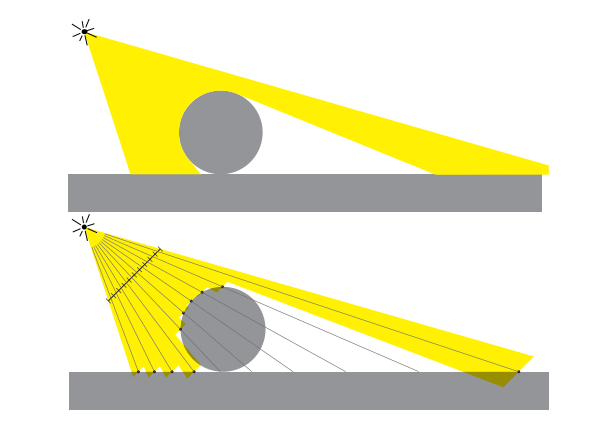
可以想象，若將一臺相機擺放在點光源位置，觀測方向沿著點光源照射方向，那麽相機所拍到的可見物體表面就是能被點光源照亮的位置。對於相機而言，我們需要知道哪些物體能夠被相機拍攝到；對於陰影，我們需要知道哪些物體能夠被光源照射到。這兩者的解決方法是類似的：利用深度圖(depth map)記錄一簇射綫到物體表面的最近距離。在第八章中，我們稱它為z-buffer，在本節中，我們稱它為shadow map。兩者不同之處在於：z-buffer要在渲染過程持續更新，而shadow map記錄了場景中到最近表面的距離。

shadow map可在渲染前計算好——光柵化整個場景，獲得深度圖。在進行普通渲染時，當需要知道該位置是否可見，就可以將其映射shadow map上查詢，得到值$d_{map}$，將它和真實距離$d$比較。如果距離相同，則該位置不在陰影中；如果$d > d_{map}$，説明物體表面接近光源，所以該位置位於陰影中。

這裏需要注意， 由於誤差的存在，判斷距離相同時，只能判斷$d$和$d_{map}$近似相等，即$d \approx d_{map}$，所以我們會定義一個容差$\epsilon$，只要$d - d_{map} < \epsilon$説明該位置能被照亮。這個容差$\epsilon$稱爲shadow bias。

還有需要注意的是，對於shadow map很少使用插值，雖然在光滑區域能獲得很好的效果，但是在邊界位置就存在嚴重缺陷，因爲邊界位置深度值會發生劇烈變化。基於這種原因，利用shadow map時通常使用最近鄰重建。爲了消除走樣現象，會采用Percentage closer filtering。

11.4.5 Environment Maps - 環境貼圖

正如利用紋理圖在shading時，不用增加模型複雜度而添加細節的做法一樣，在illumination時，同樣可以不用構建複雜的光路幾何而獲取細節。因爲，儅光源離物體較遠時（相對於物體尺寸），我們假設不同位置的光照變化非常小，因此可以只關心光照方向而不用在意它的變化，這種僅依賴光照方向情況可以使用環境貼圖(environment map)實現。

環境貼圖的主要方法是，將信息記錄在一個球體上，類似查詢顔色信息，但我們并不準確的獲得從三維空間中映射到紋理圖上的點，而是計算得到表示光照方向的信息。一個簡單的應用函數如下，用來查詢光纖追蹤獲得的顔色信息：

利用環境貼圖后，在光纖追蹤時，表面光滑的物體就能夠反射出背景環境。相同的效果也可以通過在光柵化時，利用著色器實現。

更高級的應用可以獲得所有光照情況而不僅僅是鏡面反射。若是利用光纖追蹤器計算，需要利用蒙特卡洛積分；若是在光柵化階段計算，則需要計算多個點光源和多個陰影貼圖的叠加結果。

前面提到環境貼圖的信息是記錄在球體上，所以它在球體兩極位置會存在失真現象。所以，cubemaps作爲有效的存儲手段得到廣汎的應用。

11.5 Procedural 3D Textures

在前面章節中，我們使用$c_r$表示物體表面的漫反射係數，但是物體表面漫反射係數并非是個固定值，所以我們利用函數$c_r(\mathbf{p})$來表示，其中$\mathbf{p}$表示三維空間中的位置，$c_r(\mathbf{p})$是從三維空間點到類似RGB值得映射。這樣，對於帶有紋理的物體，反射係數就能隨著位置的變化而變化。

還有一種方式就是直接創建三維紋理圖，即為三位空間中所有點都定義一個反射係數值，之後只需要通過$\mathbf{p}$直接查詢獲得。這種方式有時比創建二維紋理圖有效的多，特別是對於由實體介質雕刻出的表面，例如大理石雕刻。當然，這種方式也有個致命缺陷——内存開銷巨大，因爲這個缺陷，我們實際中并不直接使用三維紋理，而是用過程紋理(procedure textures)，這個方式然我們使用數學手段而不是查詢的方式來獲得紋理值。下面就將介紹幾種定義過程紋理的基本工具。

11.5.1 3D Stripe Textures - 三維條紋紋理

假設定義兩種顔色$c_0$和$c_1$，爲了獲得條紋，還需要定義一個振蕩函數來切換這兩種顔色。一個簡單的函數就是$sin$函數(正弦函數)。

同樣，我們可以加入$w$用於控制條紋寬度

如果希望條紋閒能有漸變效果，則可以加入參數$t$將顔色進行綫性變化。

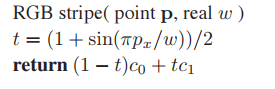
上面提到的三種效果如下圖所示。

11.5.2 Solid Noise - 實體噪聲

儘管條紋紋理已經非常有用了，但是有時我們希望獲得類似鳥蛋表面的斑駁紋理，這通常能用一種實體噪聲來實現，通常也被稱為Perlin noise。

爲了獲得具有噪聲的外觀，直覺上是利用隨機函數為每個點都分配一個隨機值，最終能夠獲得類似“白噪聲”的結果，但是這個結果不夠平滑，我們希望的結果是具有一定平滑性，但又不能喪失隨機性。

一種至今都未實現的做法是對白噪聲進行模糊化操作。

另一種方式是構建一個柵格矩陣，每個柵格點都分配一個隨機值，利用插值的方式獲得柵格閒的點的信息。這個方式讓柵格變得明顯，爲了讓柵格并不突顯，Perlin利用一系列技巧來改善基本的柵格技術，本質上只對三維隨機數數組的綫性插值做了三個改動：第一個改動是使用Hermite插值來消除馬赫條帶(mach bands)；第二個改動是使用隨機向量而不是數值，利用點乘得到一個隨機數；這樣就能把局部最小值和最大值的點從柵格上移開，使得基本的柵格結構更不明顯；第三個改動是使用一維數組和散列表創建虛擬的隨機向量三維數組，這增加了計算量而降低了内存使用率。下面給出Perlin的基本方法的數學表示： $$ n(x,y,z) = \sum_{i=\lfloor{x\rfloor}}^{\lfloor{x\rfloor}+1}\sum_{j=\lfloor{y\rfloor}}^{\lfloor{y\rfloor}+1}\sum_{k=\lfloor{z\rfloor}}^{\lfloor{z\rfloor}+1}\Omega_{ijk}(x-i, y-j, z-k) $$

其中，$(x,y,z)$是笛卡爾坐標系下的$\mathbf{x}$坐標，并且 $$ \Omega_{ijk}(u,v,w) = \omega(u)\omega(v)\omega(w)(\Gamma_{ijk}\cdot(u,v,w)) $$

其中，$\omega(t)$是一個三次權重函數

$$ \omega(t) = \begin{cases} 2|t|^3 - 3|t|^2 + 1 & \text{if } |t| < 1, \\[2ex] 0 & \text{otherwise}. \end{cases} $$

最後一部分，$\Gamma_{ijk}$是一個關於柵格點$(x,y,z) = (i,j,k)$的隨機單位向量。因爲要得到任意$ijk$下的結果，所以使用一個僞隨機表： $$ \Gamma_{ijk} = \mathbf{G}(\phi{(i + \phi{(j + \phi{(k)})})}) $$

其中， $\mathbf{G}$是預先計算好的$n$哥隨機單位向量數組，這樣$\phi(i) = \mathbf{P}[i\ mod\ n]$，這裏的$\mathbf{P}$是一個長度為$n$的$0 \sim n-1$的整型數組。計算$\mathbf{G} = (v_x, v_y, v_z)$的方式是：

$$ v_x = 2\xi -1\\ v_y = 2\xi' - 1\\ v_z = 2\xi'' - 1\\ $$

其中，$\xi, \xi’, \xi’’ $是歸一化到區間$[0,1]$上的隨機數。若$(v_x^2 + v_y^2 + v_z^2) < 1$，則把向量歸一化為單位向量，否則隨機設置該向量直到$(v_x^2 + v_y^2+v_z^2)<1$，然後再將其歸一化為單位向量。

因爲實體噪聲值可以爲正也可以為負，所以把它轉換為顔色之前必須先進行變換。下圖展示了一個$10 \times 10$區域中的噪聲絕對值，另外還有$x$方向和$y$方向拉伸的結果。其中深色曲綫是原來噪聲函數由正轉負的地方。

因爲噪聲是在$[-1,1]$閒變化，所以用$(noise + 1) * \sigma$作爲顔色可以得到更平滑的圖像，改變縮放係數$\sigma$可以得到不同對比度的圖片。下圖展示了$\sigma = 0.5$和$\sigma = 0.8$的結果。

11.5.3 Turbulence - 擾動

許多自然紋理包含不同尺寸的自相似紋理。Perlin使用一種偽分形“擾動”函數實現： $$ n_t(\mathbf{x}) = \sum_{i}\frac{|n(2^i\mathbf{x})|}{2^i} $$

這樣就能有效的在自身上反復叠加經過縮放后的噪聲函數，如下圖所示。

利用擾動對之前的條紋進行變形可得：

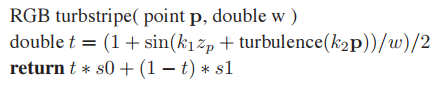
利用不同$k_1$和$k_2$值能得到不同結果。

Frequently Asked Questions

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。