6.1 2D-綫性變換

6.1.1 Scaling

$$ scale(s_x, s_y) = \begin{bmatrix} s_x,& 0 \\
0,& s_y \end{bmatrix} $$

6.1.2 Shearing

$$ shear_x(s) = \begin{bmatrix} 1,& s\\
0,& 1 \end{bmatrix} = \begin{bmatrix} 1,& \tan{\phi}\\
0,& 1 \end{bmatrix} $$ $$ shear_y(s) = \begin{bmatrix} 1, & 0\\
s, & 1 \end{bmatrix} = \begin{bmatrix} 1,& 0\\
\tan{\phi},& 1 \end{bmatrix} $$

6.1.3 Rotation

$\phi$逆時針爲正，順時針為負。 $$ rotate(\phi) = \begin{bmatrix} \cos{\phi},&-\sin{\phi}\\
\sin{\phi},&\cos{\phi} \end{bmatrix} $$ 旋转矩阵有一个很好的特性 $$ R^T = \begin{bmatrix} \cos{\phi},&\sin{\phi}\\
-\sin{\phi},&\cos{\phi} \end{bmatrix} = R^{-1} $$

6.1.4 Reflection

$$ \text{reflect-x} = \begin{bmatrix} 1,&0\\
0,&-1 \end{bmatrix} $$ $$ \text{reflect-y} = \begin{bmatrix} -1,&0\\
0,&1 \end{bmatrix} $$

6.1.5 變換的組合

例如有scale變換$\mathbf{S}$和旋轉變換$\mathbf{R}$，那麽可以將這兩種變換組合成一個變換矩陣$\mathbf{M}$作用於目標上，$\mathbf{M} = \mathbf{R} \mathbf{S}$。這種組合對順序有嚴格要求，變換從右到左先後進行，换句话说就是，矩阵乘法不满足交换律。

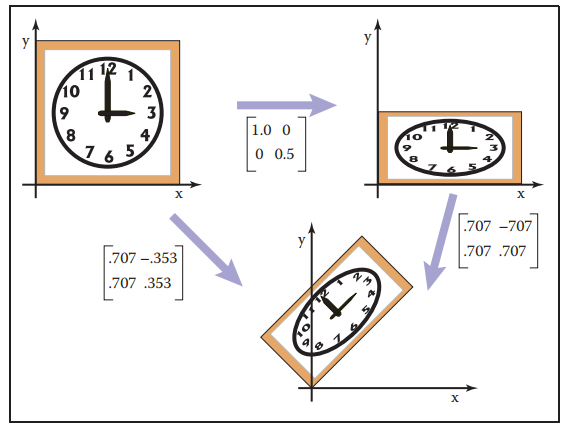
从旋转和缩放两个变换理论上可构造出任意的线性变换，这对于之后的变换拆解有一定指导意义。

6.1.6 變換的拆解

Symmetric Eigenvalue Decomposition

任意对称矩阵$\mathbf{A}$，都能使用特徵值分解成如下形式： $$ \mathbf{A} = \mathbf{R}\mathbf{S}\mathbf{R}^T $$ 其中，$\mathbf{R}$是單位正交矩陣，由矩陣$\mathbf{A}$的特徵向量構成，$\mathbf{S}$是特徵值構成的對角矩陣。再假設矩陣$\mathbf{R}$的列向量為$v_1$、$v_2$，矩陣$\mathbf{A}$特徵值為$\lambda_1$、$\lambda_2$。

從幾何角度分析等式$\mathbf{A} = \mathbf{R}\mathbf{S}\mathbf{R}^T$：

  1. 旋轉$v_1$和$v_2$至$x$軸和$y$軸（$\mathbf{R}^T$）；
  2. 按($\lambda_1, \lambda_2$)縮放$x$和$y$（$\mathbf{S}$）；
  3. 旋轉$x$軸和$y$軸囘原來的位置（$\mathbf{R}$）

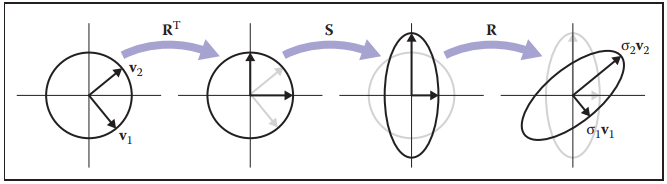
從以上分析可以看出，對於對稱矩陣，幾何上其實只是做了縮放操作，而這個縮放操作可以是非軸向且不均匀的。

再從旋轉和縮放組合後的矩陣驗證：

$$ \mathbf{R}\mathbf{S}\mathbf{R}^T = \begin{bmatrix} \cos{\phi},&-\sin{\phi}\\\\ \sin{\phi},&\cos{\phi} \end{bmatrix} \begin{bmatrix} \lambda_1,&0\\\\ 0,&\lambda_2 \end{bmatrix} \begin{bmatrix} \cos{\phi},&\sin{\phi}\\\\ -\sin{\phi},&\cos{\phi} \end{bmatrix} = \\\\ \begin{bmatrix} \lambda_1\cos^2{\phi} + \lambda_2\sin^2{\phi},&(\lambda_2 - \lambda_1)\cos{\phi}\sin{\phi}\\\\ (\lambda_2 - \lambda_1)\cos{\phi}\sin{\phi},&\lambda_2\cos^2{\phi} + \lambda_1\sin^2{\phi} \end{bmatrix} $$

Singular Value Decomposition

對於非對稱矩陣，SVD分解同樣也能獲得相應的效果 $$ \mathbf{A} = \mathbf{U}\mathbf{S}\mathbf{V}^T $$ 其中，相較於特徵值分解中單個旋轉矩陣$\mathbf{R}$，這裏使用矩陣$\mathbf{U}$和矩陣$\mathbf{V}$，矩陣$\mathbf{U}$由左奇異向量$\mathbf{u}_i$構成，矩陣$\mathbf{V}$由右奇異向量$\mathbf{v}_i$構成，而對角矩陣$\mathbf{S}$是由奇異值構成。

從幾何角度分析奇異值分解$\mathbf{A} = \mathbf{U}\mathbf{S}\mathbf{V}^T$：

  1. 旋轉$\mathbf{v}_1$和$\mathbf{v}_2$至$x$軸和$y$軸（$\mathbf{V}^T$）；
  2. 按($\sigma_1, \sigma_2$)縮放$x$和$y$（$\mathbf{S}$）；
  3. 旋轉$x$軸和$y$軸至$\mathbf{u}_1$和$\mathbf{u}_2$（$\mathbf{U}$）

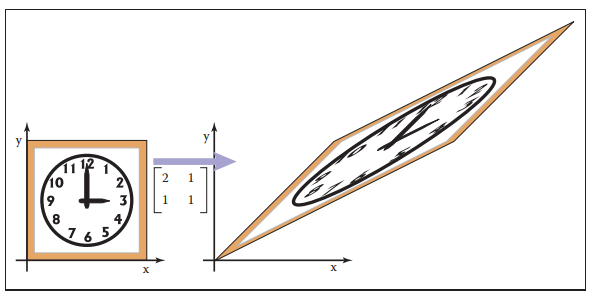
奇異值分解與特徵值分解的區別除了兩個不同的正交矩陣和單個旋轉矩陣外，還有另外一個區別。由於奇異值分解后有不同的奇異值向量，我們可以通過翻轉符號來保持奇異值非負，同時需要翻轉奇異值向量的方向來保證結果不變，這樣就導致矩陣$\mathbf{U}$和矩陣$\mathbf{V}$不再是單純的旋轉矩陣，它們還包含了$reflection$操作。雖然看起來在使用過程中不太方便，但是通過矩陣的行列式的值就能判斷是旋轉（$+1$）還是鏡像（$-1$）。

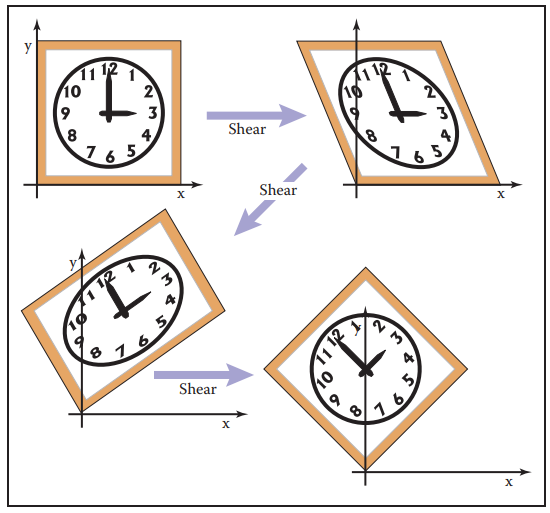
Paeth Decomposition of Rotations

旋轉矩陣可分解爲一系列斜切操作：

$$ \begin{bmatrix} \cos{\phi},&-\sin{\phi}\\\\ \sin{\phi},&\cos{\phi} \end{bmatrix} = \begin{bmatrix} 1,&\frac{\cos{\phi}-1}{\sin{\phi}}\\\\ 0,&1 \end{bmatrix} \begin{bmatrix} 1,&0\\ \sin{\phi},&1 \end{bmatrix} \begin{bmatrix} 1,&\frac{\cos{\phi}-1}{\sin{\phi}}\\\\ 0,&1 \end{bmatrix} $$

6.2 3D-綫性變換

類似2D的綫性變換，其中旋轉操作因爲多了兩個自由度，所以略有不同： $$ \begin{align} \text{scale}(s_x, s_y, s_z) &= \begin{bmatrix} s_x & 0 & 0\\
0 & s_y & 0\\
0 & 0 & s_z \end{bmatrix} \\[3ex] \text{rotate-z}(\alpha) &= \begin{bmatrix} \cos{\alpha} & -\sin{\alpha} & 0\\
\sin{\alpha} & \cos{\alpha} & 0\\
0 & 0 & 1 \end{bmatrix} \\[3ex] \text{rotate-x}(\beta) &= \begin{bmatrix} 1 & 0 & 0\\
0 & \cos{\beta} & -\sin{\beta}\\
0 & \sin{\beta} & \cos{\beta} \end{bmatrix} \\[3ex] \text{rotate-y}(\gamma) &= \begin{bmatrix} \cos{\gamma} & 0 & \sin{\gamma}\\
0 & 1 & 0\\
-\sin{\gamma} & 0 & \cos{\gamma} \end{bmatrix} \\[3ex] \text{shear-x}(d_y, d_z) &= \begin{bmatrix} 1 & d_y & d_z\\
0 & 1 & 0\\
0 & 0 & 1 \end{bmatrix} \\[3ex] \text{shear-y}(d_x, d_z) &= \begin{bmatrix} 1 & 0 & 0\\
d_x & 1 & d_z\\
0 & 0 & 1 \end{bmatrix} \\[3ex] \text{shear-z}(d_x, d_y) &= \begin{bmatrix} 1 & 0 & 0\\
0 & 1 & 0\\
d_x & d_y & 1 \end{bmatrix} \end{align} $$

與2D綫性變換類型，3D綫性變換也能通過矩陣乘法將多種變換組合成一個矩陣，同樣也能通過SVD變換將變換矩陣分解成任意旋轉和縮放；3D旋轉也同樣能分解成3D錯切變換的組合。

6.2.1 任意3D旋轉

通過上面三個軸的旋轉矩陣可以發現，3D旋轉矩陣是正交陣，現假設笛卡爾坐標系下，三軸為$\mathbf{x}$、$\mathbf{y}$和$\mathbf{z}$ ，可以通過一個旋轉矩陣$\mathbf{R}_{uvw}$獲得新的基坐標軸$\mathbf{u}$, $\mathbf{v}$和$\mathbf{w}$，這三個基坐標軸滿足：

$$ \begin{align} \mathbf{u} &= x_u\mathbf{x} + y_u\mathbf{y} + z_u\mathbf{z} \\[2ex] \mathbf{v} &= x_v\mathbf{x} + y_v\mathbf{y} + z_v\mathbf{z} \\[2ex] \mathbf{w} &= x_w\mathbf{x} + y_w\mathbf{y} + z_w\mathbf{z} \\[2ex] \mathbf{u}\cdot\mathbf{u} &= \mathbf{v}\cdot\mathbf{v} = \mathbf{w}\cdot \mathbf{w} = 1 \\[2ex] \mathbf{u}\cdot\mathbf{v} &= \mathbf{v}\cdot\mathbf{w} = \mathbf{w}\cdot \mathbf{u} = 0 \end{align} $$

這個旋轉矩陣$\mathbf{R}_{uvw}$就可用如下方式表示：

$$ \mathbf{R}_{uvw} = \begin{bmatrix} x_u & y_u & z_u\\ x_v & y_v & z_v\\ x_w & y_w & z_w \end{bmatrix} $$

很容易驗證得出：

$$ \mathbf{R}_{uvw}\mathbf{u} = \begin{bmatrix} \mathbf{u}\cdot \mathbf{u}\\ \mathbf{u}\cdot\mathbf{v}\\ \mathbf{u}\cdot\mathbf{w} \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0 \end{bmatrix} = \mathbf{x} $$

同理可得：

$$ \begin{align} \mathbf{R}_{uvw}\mathbf{v} &= \mathbf{y}\\ \mathbf{R}_{uvw}\mathbf{w} &= \mathbf{z} \end{align} $$

由於$\mathbf{R}_{uvw}$是正交矩陣，那麽$\mathbf{R}^T = \mathbf{R}^{-1}$，這就説明：

$$ \begin{align} \mathbf{R}_{uvw}^T\mathbf{x} &= \mathbf{u} \\ \mathbf{R}_{uvw}^T\mathbf{y} &= \mathbf{v} \\ \mathbf{R}_{uvw}^T\mathbf{z} &= \mathbf{w} \end{align} $$

舉例：假設需要將物體繞坐標系$\mathbf{xyz}$下的任一向量$\mathbf{a}$旋轉$\phi$度，該旋轉矩陣如何求？ 解答：先令$\mathbf{w} = \mathbf{a}$，再通過單向量構建基向量的方式構建出$\mathbf{u}$和$\mathbf{v}$，然後先將物體旋轉至基向量$\mathbf{uvw}$的坐標系下，再用繞$\mathbf{z}$軸的旋轉矩陣進行變換，最後變換囘原坐標係$\mathbf{xyz}$下即可，變換矩陣為：

$$ \begin{bmatrix} x_u & x_v & x_w\\ y_u & y_v & y_w\\ z_u & z_v & z_w \end{bmatrix} \begin{bmatrix} \cos{\phi} & -\sin{\phi} & 0\\ \sin{\phi} & \cos{\phi} & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_u & y_u & z_u\\ x_v & y_v & z_v\\ x_w & y_w & z_w \end{bmatrix} $$

**這個例子説明在空間中繞旋轉任意軸旋轉，可以先構造新的坐標系，將現有坐標系變換到新坐標系后，再做旋轉，最後變換囘原坐標系。**

6.2.2 Transforming Normal Vectors

對於3維向量，可以表示位置、偏移量、方向等，同樣也可以用於表示物體表面的法向量。表面法向量垂直于該位置表面的切平面。而在對3維表面進行變換時，表面法向量若使用相同的變換矩陣往往會得到與其定義不一樣的結果，即變換後的法向量不垂直與切平面。如下圖：

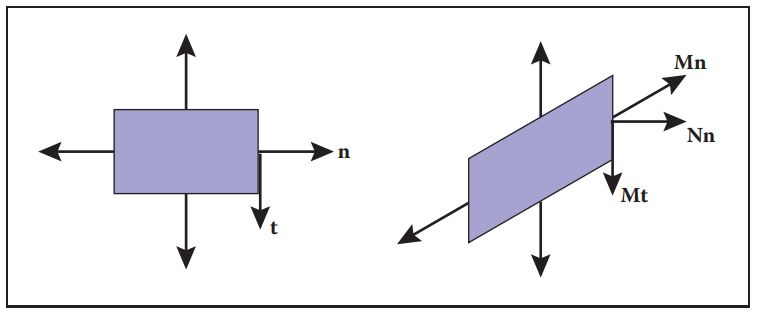
為解決該問題，需要重新推到一個變換矩陣$\mathbf{N}$，使其作用於法向量$\mathbf{n}$后，法向量$\mathbf{n}$依然垂直於切平面。假設物體變換矩陣為$\mathbf{M}$，切向量為$\mathbf{t}$，變換後的切向量為$\mathbf{t}_{M} = \mathbf{M}\mathbf{t}$，法向量為$\mathbf{n}_N = \mathbf{N}\mathbf{n}$。現要滿足一下等式：
$$ \mathbf{n}_N^T\mathbf{t}_{M} = 0 $$

先從原始等式$\mathbf{n}^T \mathbf{t} = 0$出發，令$\mathbf{I} = \mathbf{M}^{-1}\mathbf{M}$:

$$ \begin{align} &\mathbf{n}^T\mathbf{t} = \mathbf{n}^T\mathbf{I}\mathbf{t} = \mathbf{n}^T\mathbf{M}^{-1}\mathbf{M}\mathbf{t} = 0 \\ \Rightarrow &\left(\mathbf{n}^T\mathbf{M}^{-1}\right)\left(\mathbf{M}\mathbf{t}\right) = \left(\mathbf{n}^T\mathbf{M}^{-1}\right)\mathbf{t}_M = 0 \end{align} $$

這樣可得到：

$$ \begin{align} \mathbf{n}_N^T &= \mathbf{n}^T\mathbf{M}^{-1}\\ \Rightarrow \mathbf{n}_N &= \left(\mathbf{n}^T\mathbf{M}^{-1}\right)^T = \left(\mathbf{M}^{-1}\right)^T\mathbf{n} \end{align} $$

這樣就可以得到我們需要的$\mathbf{N} = \left(\mathbf{M}^{-1}\right)^T$。 還可以進一步簡化，由於對於法向量，我們只使用其方向，而不關心其長度，所以在計算$\mathbf{N}$時可以忽略矩陣逆變換的行列式計算，這樣就能得到$\mathbf{N}$的值爲：

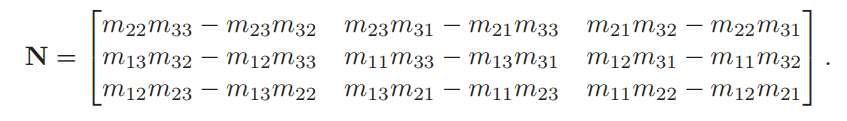
6.3 平移和仿射變換

前面介紹的利用矩陣對物體進行變換，只能實現縮放和旋轉操作，無法實現平移。若要實現平移，需要在之後添加平移向量。

$$ \begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} m_{00} & m_{01}\\ m_{10} & m_{11} \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} + \begin{bmatrix} x_t\\ y_t \end{bmatrix} $$

這樣表示顯然不夠優雅，我們希望用一個矩陣就能同時實現綫性變換和平移變換。爲達到這個目的，齊次坐標表示就顯得非常有用。將二維空間中的點用三維向量表示，就可實現：

$$ \begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} = \begin{bmatrix} m_{00} & m_{01} & x_t\\ m_{10} & m_{11} & y_t\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} $$

之後就將這種合并了綫性變換和平移變換的矩陣統稱為仿射變換矩陣(Affine Transformation)。 齊次坐標表示有兩種：$\begin{bmatrix}x\\y\\1\end{bmatrix}$和$\begin{bmatrix}x\\y\\0\end{bmatrix}$，前者表示點的位置，後者表示方向或位移。 同樣，利用矩陣乘法，也能將平移變換和綫性變換組合成一個矩陣形式，而單純的平移變換矩陣如下：

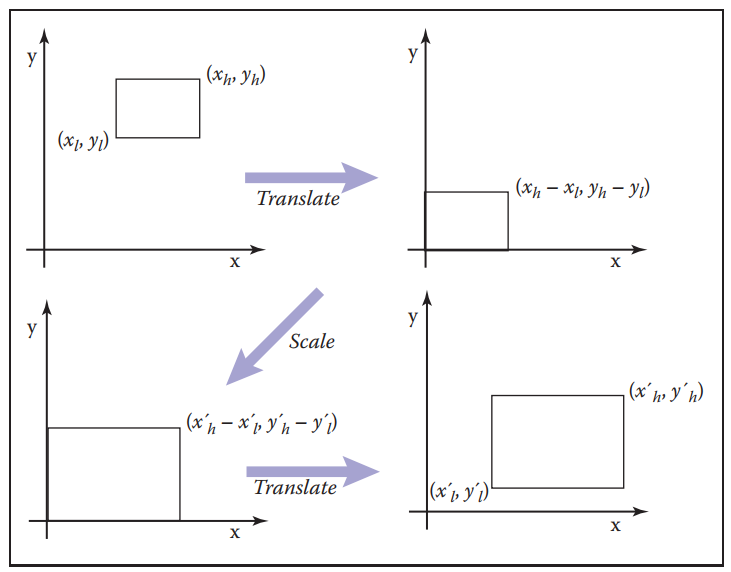
$$ \text{translate}(x_t, y_t, z_t) = \begin{bmatrix} 1 & 0 & 0 & x_t\\ 0 & 1 & 0 & y_t\\ 0 & 0 & 1 & z_t\\ 0 & 0 & 0 & 1 \end{bmatrix} $$

例如，對下圖窗口進行一系列變換：

$$ \begin{align} \text{window} &= \text{translate}(x_l',y_l')\text{scale}\left(\frac{x_h' - x_l'}{x_h-x_l}, \frac{y_h'-y_l'}{y_h-y_l}\right)\text{translate}(-x_l,-y_l)\\ &= \begin{bmatrix} 1 & 0 & x_l'\\ 0 & 1 & y_l'\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{x_h' - x_l'}{x_h-x_l} & 0 & 0\\ 0 & \frac{y_h'-y_l'}{y_h-y_l} & 0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -x_l\\ 0 & 1 & -y_l\\ 0 & 0 & 1 \end{bmatrix}\\ & = \begin{bmatrix} \frac{x_h' - x_l'}{x_h-x_l} & 0 & \frac{x_l'x_h - x_h'x_l}{x_h - x_l}\\ 0 & \frac{y_h'-y_l'}{y_h-y_l} & \frac{y_l'y_h - y_h'y_l}{y_h-y_l}\\ 0 & 0 & 1 \end{bmatrix} \end{align} $$

6.4 變換矩陣的逆

從幾何角度看：

$$ \begin{align} \text{scale}(s_x, s_y, s_z)^{-1} &= \text{scale}(1/s_x, 1/s_y, 1/s_z)\\[2ex] \text{rotate}(\phi)^{-1} &= \text{rotate}(-\phi)\\[2ex] \text{translate}(x_t,y_t,z_t)^{-1} &= \text{translate}(-x_t,-y_t,-z_t) \end{align} $$

而對於一系列變換組合

$$ \mathbf{M} = \mathbf{M}_{1}\mathbf{M}_{2}\cdots\mathbf{M}_n $$
其逆變換為
$$ \mathbf{M}^{-1} = \mathbf{M}_n^{-1}\cdots\mathbf{M}_{2}^{-1}\mathbf{M}_{1}^{-1} $$

同樣也能使用SVD分解來求逆變換，例如，已知變換$\mathbf{M}$：

$$ \mathbf{M} = \mathbf{R}_1\text{scale}(\sigma_1,\sigma_2,\sigma_3)\mathbf{R}_3 $$

利用SVD分解特性和逆變換規則可得：

$$ \mathbf{M}^{-1} = \mathbf{R}_2^T\text{scale}(1/\sigma_1, 1/\sigma_2, 1/\sigma_3)\mathbf{R}_1^T $$

6.5 坐標系變換

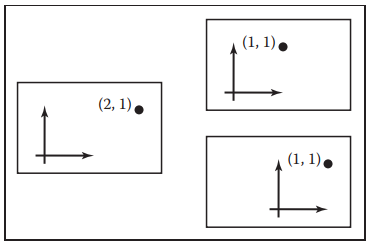
之前所説的變換，坐標系都是固定的，變換都是作用於物體上；本節是固定物體，通過變換坐標系來獲得相同的結果。如下圖，清晰的展示了兩種方法的區別：

幾何中，定義坐標系需要定義原點$\mathbf{p}$和基向量{$\mathbf{u},\mathbf{v},\mathbf{w}$}，該坐標系上所有的點（$u, v, w$）都能用以下方式表示：

$$ \mathbf{p} + u\mathbf{u} + v\mathbf{v} + w\mathbf{w} $$

通常三個基向量會選取正交向量。2D情況類似。下面就在2D下舉例説明：

如圖所示，點$\mathbf{p}$在$xoy$坐標系下表示爲：

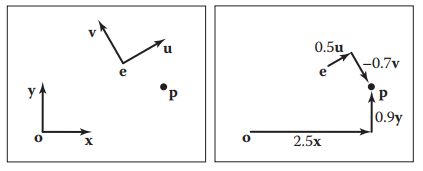
$$ \mathbf{p} = (x_p,y_p) \equiv \mathbf{o} + x_p\mathbf{x} + y_p\mathbf{y} $$

在坐標系$uev$下，表示為：

$$ \mathbf{p} = (u_p, v_p) \equiv \mathbf{e} + u_p\mathbf{u} + v_p\mathbf{v} $$

我們可以通過以下變換，將點$\mathbf{p}$坐標在兩個坐標系閒切換：

$$ \begin{align} &\begin{bmatrix} x_p\\ y_p\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & x_e\\ 0 & 1 & y_e\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_u & x_v & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p\\ v_p\\ 1 \end{bmatrix} = \begin{bmatrix} x_u & x_v & x_e\\ y_u & y_v & y_e\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} u_p\\ v_p\\ 1 \end{bmatrix} \\ \Rightarrow &\mathbf{P}_{xy} = \begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{e}\\ 0 & 0 & 1 \end{bmatrix}\mathbf{P}_{uv} \end{align} $$

上面這種坐標系閒變換的矩陣稱爲frame-to-canonical矩陣。

frame-to-canonical解釋如下：It takes points expressed in the (u, v) frame and converts them to the same points expressed in the canonical frame.

同樣，其逆變換如下：

$$ \begin{align} &\begin{bmatrix} u_p\\ v_p\\ 1 \end{bmatrix} = \begin{bmatrix} x_u & x_v & 0 \\ y_u & y_v & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -x_e\\ 0 & 1 & -y_e\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_p\\ y_p\\ 1 \end{bmatrix} \\ \Rightarrow &\mathbf{P}_{uv} = \begin{bmatrix} \mathbf{u} & \mathbf{v} & \mathbf{e}\\ 0 & 0 & 1 \end{bmatrix}^{-1}\mathbf{P}_{xy} \end{align} $$

這種逆變換稱爲canonical-to-frame矩陣。 canonical-to-frame解釋如下：It takes points expressed in the canonical frame and converts them to the same points expressed in the (u,v) frame.

因爲所有坐標系都是平等的，所以，上面的逆變換也可以寫成：

$$ \mathbf{P}_{uv} = \begin{bmatrix} \mathbf{x}_{uv} & \mathbf{y}_{uv} & \mathbf{o}_{uv}\\ 0 & 0 & 1 \end{bmatrix}\mathbf{P}_{xy} $$

FAQ

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片來自本書截圖和Games-101課件截圖。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。