4.1 - Ray Tracing算法框架

Basic Ray Tracing分为三个部分：

  1. ray generation: 计算光源位置和光线方向；
  2. ray intersection: 计算与光路相交的最近的物体；
  3. shading: 基于ray intersection计算每个点的特性，例如颜色等；

Basic ray tracing program:

4.2 - 投影

在计算机图形学中，基本都采用线性透视(linear perspective)，即从三维空间到二维空间过程中，不改变直线形状——直线依旧是直线。

平行投影 - parallel projection

根据成像平面与投影方向是否垂直又分为：正交投影和斜投影。

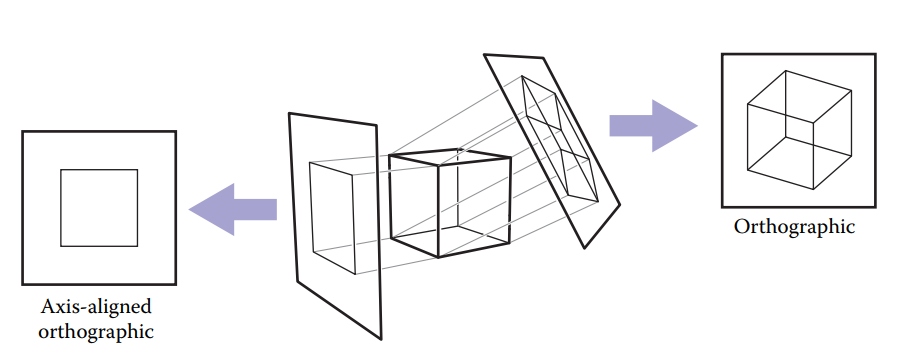
平行投影特点：

  1. 平行线依旧平行；
  2. 保留尺寸和形状；

平行投影缺点就是不真实——与现实生活中的现象不吻合。

透视投影 - perspective projection

与平行投影类似，根据成像平面与投影方向是否垂直，同样也分为：正交和倾斜的投影；

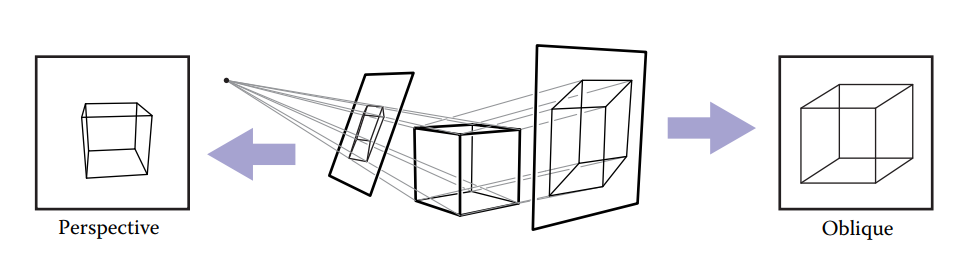
透视投影特点：

  1. 所有成像点沿投影方向能汇聚到一点——viewpoint；
  2. 平行线不再平行；

4.3 - 计算Viewing Ray

如何表示Ray

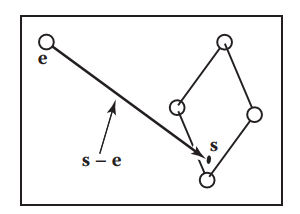
从视点$\mathbf{e}$到三维空间中某平面上的点$\mathbf{s}$的直线表示为： $$ \mathbf{p}(t) = \mathbf{e} + t(\mathbf{s} - \mathbf{e}) $$ 根据图中可对表达式解释为：``we advance from e along the vector (s − e) a fractional distance t to find the point p``。 从这个式子可以看出：
  1. $\mathbf{e}$是射线源点；
  2. $\mathbf{s}-\mathbf{e}$是射线方向；
  3. $\mathbf{p}(0) = \mathbf{e}$，$\mathbf{p}(1) = \mathbf{s}$；
  4. 如果$t < 0$，则点$\mathbf{p}(t)$在视点的后方；
  5. $\mathbf{p}(t)$单调递增，即$0<t_1<t_2$，$\mathbf{p}(t_1)$比$\mathbf{p}(t_2)$离视点近；

构建相机坐标系(camera frame)：

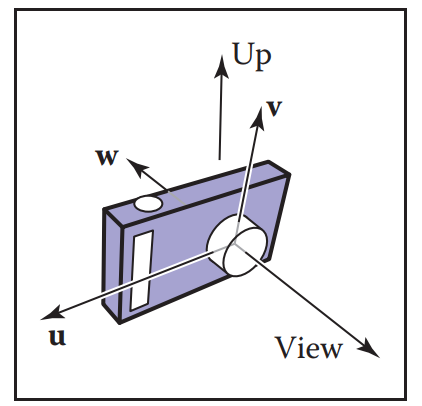
正交视图

假设图像上下左右边界分别为：$t$、$b$、$l$、$r$。通常$l < 0 < r$、$b < 0 < t$。如下图：

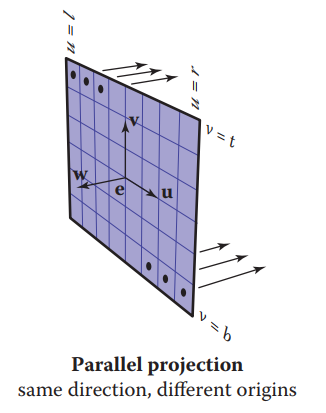
图像上任意点坐标$(u, v)$可以通过这四个变量计算得到： $$ \begin{split} u = l + \frac{(r - l)(i + 0.5)}{n_x} \\[2ex] v = b + \frac{(t-b)(j+0.5)}{n_y} \end{split}\tag{4.1} $$ 其中，$n_x$和$n_y$分别为图像的宽高。

对于平行投影的Ray可以按如下方法计算：

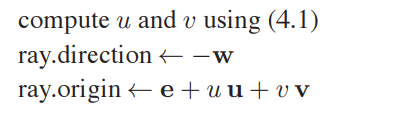
对于斜平行投影，只需要改变$ray.direction = -\mathbf{w}$为斜视图投影方向$ray.direction = \mathbf{d}$即可。计算$\mathbf{u}$和$\mathbf{v}$依然要使用$\mathbf{w}$。

透视视图

对于透视视图，所有的rays都会交于视点。视点与图像平面的距离$d$通常也可称为焦长。

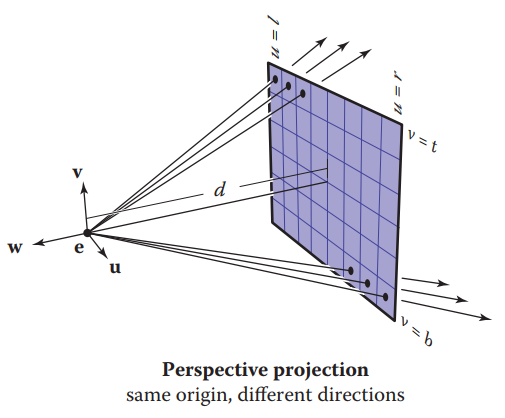
对于透视视图正交的Ray计算，可按如下方式进行：

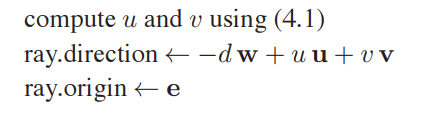
同样，在进行斜投影时，只需将$ray.direction$中的$-d\mathbf{w}$替换为$d\mathbf{d}$即可。

4.4 Ray-Object Intersection

生成Ray方程$\mathbf{e}+t\mathbf{d}$后，需要计算与Ray最先相交的物体在哪里，其中$t > 0$。通常解决这个问题会为$t$设定一个区间$[t_1,t_2]$；若一般化的话，令$t_1 = 0$，$t_2 = +\infty$。

4.4.1 Ray-Sphere相交

假設ray函數表達為 $$ \mathbf{p}(t) = \mathbf{e} + t\mathbf{d} $$ 球面隱式函數為 $$ f(\mathbf{p}) = (x - x_c)^2 + (y - y_c)^2 + (z - z_c)^2 - R^2 = 0 $$ 兩者交點必須滿足以上兩個方程，因此任意一點$\mathbf{p}$滿足以上兩個方程，就説明該點為兩者交點，用向量形式表示為：

$$ \begin{align} (\mathbf{p} - \mathbf{c})\cdot (\mathbf{p} - \mathbf{c}) - R^2 &= 0 \\ \Rightarrow (\mathbf{e} + t\mathbf{d} - \mathbf{c})\cdot(\mathbf{e} + t\mathbf{d} - \mathbf{c}) - R^2 &= 0 \\ \Rightarrow (\mathbf{d}\cdot\mathbf{d})t^2 + 2\mathbf{d}\cdot(\mathbf{e} - \mathbf{c})t + (\mathbf{e} - \mathbf{c})\cdot(\mathbf{e} - \mathbf{c}) - R^2 &= 0 \end{align} $$

根據一元二次方程的解可知： $$ t = \frac{-\mathbf{d}\cdot(\mathbf{e} - \mathbf{c}) \pm \sqrt{(\mathbf{d}\cdot(\mathbf{e} - \mathbf{c}))^2 - (\mathbf{d}\cdot\mathbf{d})((\mathbf{e} - \mathbf{c})\cdot(\mathbf{e} - \mathbf{c}) - R^2)}}{(\mathbf{d}\cdot \mathbf{d})} $$

在點$\mathbf{p}$処的法向量為$\mathbf{n} = 2(\mathbf{p} - \mathbf{c})$，單位法向量為$(\mathbf{p} - \mathbf{c}) / R$。

4.4.2 Ray-Triangle相交

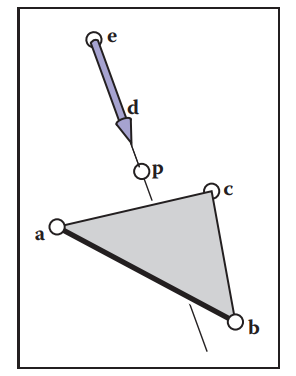
同樣，由ray函數： $$ \mathbf{p}(t) = \mathbf{e} + t\mathbf{d} $$ 和三角形函數： $$ \mathbf{p} = (1 - \beta - \gamma)\mathbf{a} + \beta\mathbf{b} + \gamma\mathbf{c} $$ 可得： $$ \mathbf{e} + t\mathbf{d} = \mathbf{a} + \beta(\mathbf{b} - \mathbf{a}) + \gamma (\mathbf{c} - \mathbf{a}) \tag{4.2} $$ 其中，$\beta > 0, \gamma > 0 , \beta+\gamma < 1$，不然ray與三角形無交點。

對於等式(4.2)，三個未知量$t,\beta, \gamma$，三個方程：

$$ \begin{align} x_e + tx_d &= x_a + \beta(x_b - x_a) + \gamma(x_c - x_a)\\ y_e + ty_d &= y_a + \beta(y_b - y_a) + \gamma(y_c - y_a)\\ z_e + tz_d &= z_a + \beta(z_b - z_a) + \gamma(z_c - z_a) \end{align} $$

利用Cramer’s Rule解方程組：

$$ \begin{bmatrix} x_a - x_b & x_a - x_c & x_d \\ y_a - y_b & y_a - y_c & y_d \\ z_a - z_b & z_a - z_c & z_d \end{bmatrix} \begin{bmatrix} \beta\\ \gamma\\ t \end{bmatrix} = \begin{bmatrix} x_a - x_e\\ y_a - y_e\\ z_a - z_e \end{bmatrix} $$

可得：

求解ray與三角形相交的僞代碼如下：

4.4.3 Ray-Polygon相交

給定平面多邊形的$m$個頂點$\mathbf{p}_1$至$\mathbf{p}_m$和表面法向量$\mathbf{n}$，那麽ray與多邊形的交點可以通過以下方式求得： $$ (\mathbf{p} - \mathbf{p}_1)\cdot \mathbf{n} = 0 $$ 將ray方程$\mathbf{p} = \mathbf{e} + t\mathbf{d}$帶入可解得： $$ t = \frac{(\mathbf{p}_1 - \mathbf{e})\cdot \mathbf{n}}{\mathbf{d}\cdot\mathbf{n}} $$ 此時求得的點$\mathbf{p}$不一定在多邊形内，所以還需進一步判斷。 判斷的方式有很多，例如將點$\mathbf{p}$和多邊形都投影到2D平面xy上，然後從點$\mathbf{p}$出發作射綫，統計該射綫與多邊形的交點個數，若爲奇數，則説明點$\mathbf{p}$在多邊形内，反之則不在。以上這個方法存在多邊形投影可能會是一條直綫，通常做法是在xy，yz或zx平面中選取一個最佳的進行投影。選取方式如下：

这部分伪代码没怎么看懂！！！

另外还有其他判断交点$\mathbf{p}$是否在多边形内的方式，例如将多边形分解成多個三角形，然後判斷點$\mathbf{p}$是否在這些三角形内。

4.4.4 與一組物體相交

大多數使用場景都不止一個物體，所以，ray的相交計算通常會獲得距離相機最近的那個物體。下面的僞代碼解釋如何在區間$[t_1,t_2]$内進行選取：

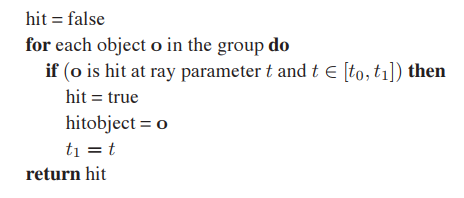
注意每次都會更改$t_1$值，讓其距離$t_0$越來越近，最終獲得$t$的最小值

4.5 Shading

經過上面一系列步驟后，可視表面的像素點就能夠確定，接下來需要利用Shading Model來計算像素值。大多數Shading Model都是描述光纖在物體表面的反射過程，因此定義一個點光源，由反射點指向光源的方向$\mathbf{l}$，觀察方向$\mathbf{v}$，反射點的表面法向量$\mathbf{n}$以及反射表面的各種特性——顔色、光澤度等。 上述所有方向向量均爲單位向量

4.5.1 Lambertian Shading

這個模型非常簡單：來自點光源的能量有多少能夠落在物體表面，與該表面和光纖方向的夾角有關。

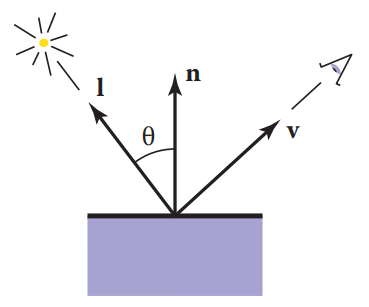
根據上圖，很容易推出Lambertian shading Model的數學表示： $$ L = k_d\cdot\mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{l})} $$ 這裏，$\mathbf{L}$就表示最終該著色點的顔色(像素值)，$k_d$表示diffuse coefficient或是表面顔色；$\mathbf{I}$表示光纖縂强度；而$\max{0, \mathbf{n}\cdot\mathbf{l}}$表示光纖與法向量夾角的$cos$值，因爲$\cos{\theta} \in [-1, 1]$，而$\cos{\theta}$在$[-1,0)$區間内，在實際中沒有意義，所以和$0$比較取最大值。

4.5.2 Blinn-Phong Shading

Lambertian Shading模型是與觀察方向無關的，這會導致使用這個模型時，在某些場景下無法準確描述真實情況，例如某些物體表面的鏡面反光。例如下圖：

爲解決這個問題，兩位大神Phong和Blinn提出一個簡單高效的鏡面高光模型。該模型的思想是，如果發生鏡面反射，那麽$\mathbf{v}$會和$\mathbf{l}$關於法向量$\mathbf{n}$對稱的向量$\mathbf{l}'$重合，那麽只要觀測方向$\mathbf{v}$越接近$\mathbf{l}'$，那麽該位置越接近鏡面反射。 爲了計算方便，大神使用了一個半向量$\mathbf{h}$用於計算，該向量的方向是$\mathbf{l}$和$\mathbf{v}$的角平分綫方向，同樣也是單位向量。那麽，只要$\mathbf{h}$越接近$\mathbf{n}$，那麽該表面就越接近鏡面反射。因此，結合前面的Lambertian Shading模型可得： $$ \mathbf{h} = \frac{\mathbf{v} + \mathbf{l}}{||\mathbf{v} + \mathbf{l}||}\\ L = k_d\cdot\mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{l})} + k_s\cdot \mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{h})}^p $$ 其中$k_s$是鏡面反射係數；這裏還引入一個新的超參數$p$，稱爲Phone exponent，通常取$p > 1$，用於控制鏡面反射衰減，也就是説，$p$值越大，發生鏡面反射的範圍越小，如下圖所示。

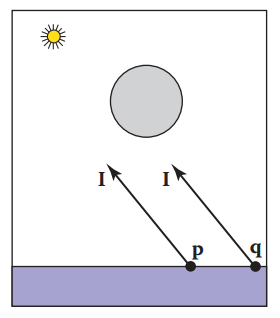
4.5.3 Ambient Shading

根據上面兩個模型可知：如果物體表面沒有接收到直接光照的話，那麽物體表面是完全黑的。但是實際中并非如此，例如：

上圖中Ambient Lighting位置是背光的，理論上應該是完全黑的，但是這裏依然能夠看清物體表面，説明依然有光纖能夠到達這個位置，這類光纖就被稱爲環境光。通常使用一個常量$I_a$來表示，爲了避免物體表面完全黑暗的情況出現。 $$ L = k_a \cdot I_a + k_d\cdot\mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{l})} + k_s\cdot \mathbf{I}\cdot\max{(0,\mathbf{n}\cdot\mathbf{h})}^p $$ 其中$k_a$稱爲surface’s ambient coefficient，$I_a$稱爲ambient light intensity。

4.5.4 多個光源

基於光的可叠加性，多個光源作用時只需要簡單叠加即可； $$ L = k_a\cdot I_a + \sum_{i = 1}^{N}[k_d\cdot\mathbf{I}_i\cdot\max{(0,\mathbf{n}\cdot\mathbf{l}_i)} + k_s\cdot \mathbf{I}_i\cdot\max{(0,\mathbf{n}\cdot\mathbf{h}_i)}^p] $$

4.6 A Ray-Tracing Program

以上已介紹了如何生成ray、如何計算和ray相交的最近物體以及如何對物體表面著色。這些流程可以按以下框架進行：

4.7 Shadows

如何判斷著色點是否在陰影中？

從著色點$\mathbf{p}$沿著光纖方向$\mathbf{l}$看，如果看到物體，則該著色點在陰影中；如果沒有存在物體，則該著色點不在陰影中。這種用於判斷是否存在陰影中的光纖稱爲``shadow rays``。 結合陰影判斷和等式(4.3)的著色模型，算法僞代碼如下：
僞代碼中，計算陰影時，$\mathbf{p}+s\mathbf{l}$區間選取為$[\epsilon, +\infty)$，其中$\epsilon$是一個非常小的正數，這麽做在數值上避免shadow rays與著色表面接觸。

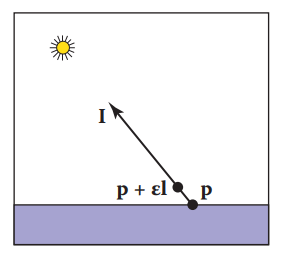
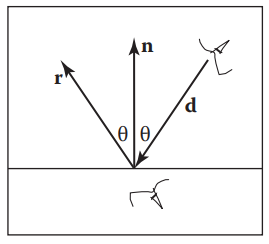
4.8 理想鏡面反射

由上圖可知，理想鏡面反射模型中，若已知入射光綫$\mathbf{d}$和入射角度$\theta$，那麽反射光綫$\mathbf{r}$可按如下方式計算得出： $$ \mathbf{r} = \mathbf{d} - 2(\mathbf{d} \cdot \mathbf{n})\mathbf{n} $$ 現實中，光綫在反射過程中會有能量損失，并且反射光的顔色也會有所不同，可以在計算顔色時遞歸調用``raycolor``： $$ color \ c = c + k_m \cdot raycolor(\mathbf{p} + s \mathbf{r}, \epsilon, \infty) $$ 其中，$k_m$是發生鏡面反射時鏡面RGB顔色係數。另外，$s \in [\epsilon, +\infty)$同樣是爲了避免計算時，反射光綫與起始位置就接觸。 這種遞歸調用可能會無限制的進行下去，爲了高效需要設定最大遞歸深度。另外可以在$k_m$不爲$0$時在進行該操作。

Frequently Asked Questions

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。