圖形學系列 Ch13-More Ray Tracing-閲讀筆記
Contents
光綫追蹤技術是產生一些高級渲染效果的基礎,在第四章已經介紹了光綫追蹤的框架,本章節將討論光綫追蹤一些有趣的使用,比如光綫與不同材質物體是如何作用的,例如光綫穿過透明物體發生的折射現象等;另外還會介紹在增加模型複雜度的同時最小化計算複雜度的兩種方法:intancing(實例化)和constructive solid geometry(CSG, 構造實體幾何)。最後,本章節還將討論分佈式光綫追蹤(distribution ray tracing)的基本框架。
13.1 Transparency and Refraction
在第四章中利用遞歸的方式計算光纖的鏡面反射,但是有些材料不僅會發生反射,同時還會發生折射,例如,鑽石、玻璃、水和空氣等。這些材料都可成爲dielectric(絕緣體)。不同的絕緣體有不同的折射係數$n$。如下表所示。

根據折射的物理現象,儅光綫從一種介質$n$進入另一種介質$n_t$時,光纖傳播方向會發生偏轉,例如下圖,根據Snell定理,假設$n_t > n$,下圖中,光綫從左側進入另一種介質:
$$
n\sin{\theta} = n_t\sin{\phi}\tag{13.1}
$$
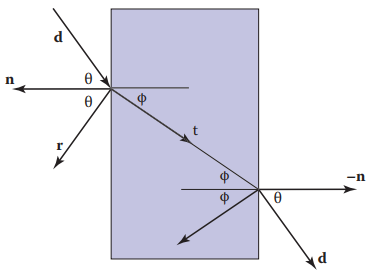
這是經典的折射定理,但在實際中,$\sin(x)$顯然沒有$\cos(x)$計算來的方便,因爲$\cos(x)$可以通過兩向量點乘獲得,所以根據三角函數$\sin^2{\theta}+\cos^2{\theta} = 1$可將公式(13.1)改寫為如下形式: $$ \cos^2{\phi} = 1 - \frac{n^2(1-\cos^2{\theta})}{n_t^2} $$
如果$n_t < n$,則是上圖中右側的傳播方式。
由於$\cos(x)$需要兩個向量點乘,所以我們將定義兩個基向量$\mathbf{n}$和$\mathbf{b}$,如下圖所示。
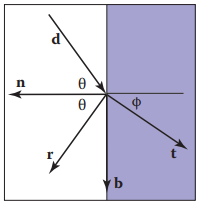
其中,光綫傳播方向$\mathbf{t}$可表示爲: $$ \mathbf{t} = \sin{\phi}\mathbf{b} - \cos{\phi}\mathbf{n} $$
同理可得: $$ \mathbf{d} = \sin{\theta}\mathbf{b} - \cos{\theta}\mathbf{n} $$
由於入射方向$\mathbf{d}$是已知的,法綫$\mathbf{n}$也是已知的,所以,基向量$\mathbf{b}$可得: $$ \mathbf{b} = \frac{\mathbf{d} + \mathbf{n}\cos{\theta}}{\sin{\theta}} $$
這樣,我們就能將傳播方向$\mathbf{t}$改寫爲向量形式。
這個公式有一個好處是,可以不關心兩種介質折射率的大小,但是,我們需要判斷根號内的式子是否非負,如果為負數時,表示沒有發生折射,所有光綫都被反射,即此時$\mathbf{t} = 0$。這種現象就稱爲total internal reflection(全内反射)。
下面討論下反射率。根據Fresnel equations,介質的反射率是隨著入射角度的變化而變化的。例如,我們在某個清澈見底的湖水邊,垂直水面看向水底,這時候我們可以知道湖水清澈見底,但是隨著我們看向湖水的角度越來越平行湖面,這時就會發現越來越難看見湖底了。這個現象可以解釋成,儅光綫垂直湖面入射時,反射較弱,折射較强;儅光綫越來越平行湖面時,反射越來越明顯,而折射越來越弱。
雖然現象是簡單的,但是Fresnel equations是非常複雜的,所以我們通常會用Schlick approximation來近視表示。
$$
R(\theta) = R_0 + (1-R_0)(1-\cos{\theta})^5
$$
其中,$R_0$表示在空氣中,光綫從法綫方向入射時的反射率。 $$ R_0 = \left(\frac{n_t-1}{n_t + 1}\right)^2 $$
而$\cos\theta$項表示入射光綫與法綫的夾角$\theta$的餘弦值。
根據Beer’s Law,儅一束光在介質中傳播時,能量是會損失的。能量損失可用如下函數表示。 $$ dI = -CIdx $$
其中$dx$表示距離,那麽解這個微分方程可得。 $$ I = k\exp{(-Cx)}\tag{13.2} $$
假設單位距離的衰減係數為$a$,那麽公式(13.2)的邊界條件為$I(0) = I_0$和$I(1) = aI(0)$。帶入公式(13.2)解得: $$ I(s) = I(0)e^{\ln{(a)}s} $$
$I(s)$表示距離入射表面$s$処的光强。
下面在代碼中添加光綫作用於透明材質的物體上,假設該物體放在空氣中,物體表面法向量方向是“朝外”的。那麽代碼如下。

這裏稍微解釋下這段代碼,在内部的條件語句$\mathbf{d}\cdot\mathbf{n} < 0$,是判斷光是從空氣中進入透明介質,還是從透明介質進入空氣。如果是從透明介質進入空氣,那麽需要計算光纖在介質中傳播時發生的能量損失。函數$refract(\mathbf{d}, \mathbf{n}, n, t)$同時計算了是否發生全反射。最後利用Schlick approximation計算反射率。最終得到著色點的RGB值。
13.2 Instancing
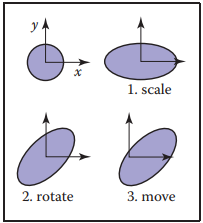
實例化instancing,假設我們需要顯示某個變形的物體,那麽直覺的做法是將物體的每個點進行變換後顯示,例如下圖中,要表示某個橢圓,我們可以將標準園進過一系列變換後獲得。這樣在存儲上,只需要存儲一個標準園和一個混合變換矩陣,這樣就得到一個物體的實例。
實例化在光綫追蹤中還有一個優勢就是讓光纖與物體相交測試變得簡單。例如,某個標準物體上有點$p$,變換矩陣為$\mathbf{M}$,光纖為$\mathbf{a} + t \mathbf{b}$,我們在做相交測試時,可以將變換矩陣的逆矩陣作用在光綫上,然後與標準物體進行相交測試,如下圖所示。
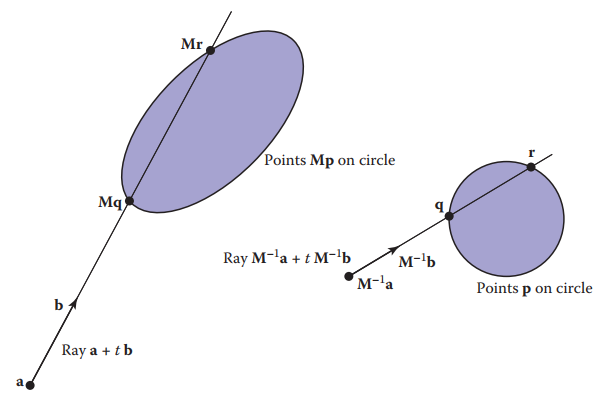
這麽做有兩個優勢:
- 與未變換的物體進行相交測試要比變換後物體來的簡單;
- 節省空間,許多變換物體可以共享相同為變換的物體。
基於這個思想,我們構建一個實例化的相交測試框架如下,另外,根據第六章中,變換前後物體表面法向量的變化可知,$n_t = (\mathbf{M}^{-1})^Tn$。
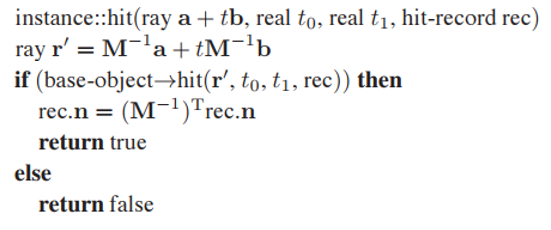
上面程序中一個非常漂亮的地方就是,參數$rec.t$不需要改變,因爲它在哪個空間中都是相同的。而另外一個重要點是,光綫方向$\mathbf{b}$不能變爲單位向量,否則上述機制就無效了。因此不需要將光綫方向限制為單位向量。
13.3 Constructive Solid Geometry
光綫追蹤另一件非常棒的事就是任何幾何基元(例如矩形、圓形等)都能無縫的加入光纖追蹤器進行直綫相交測試。這個特性就表示了直接向光綫追蹤器添加構造實體幾何(CSG)是非常簡單的。
下面先説説CSG是什麽,在說它的相交測試怎麽進行,真的非常簡單!!!
我們已經知道集合有幾種運算,例如交$\cap$、并$\cup$、非$\sim$等。那麽將這些運算運用到基本幾何形狀上就能構造出複雜的幾何形狀,如下圖所示。
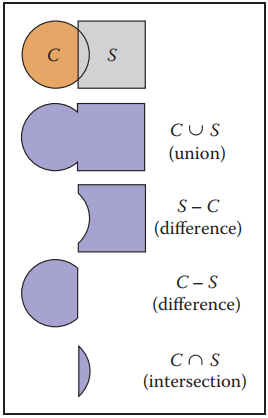
再看看CSG如何從一些幾何基元構造出複雜模型的構造樹。圖片來自維基百科
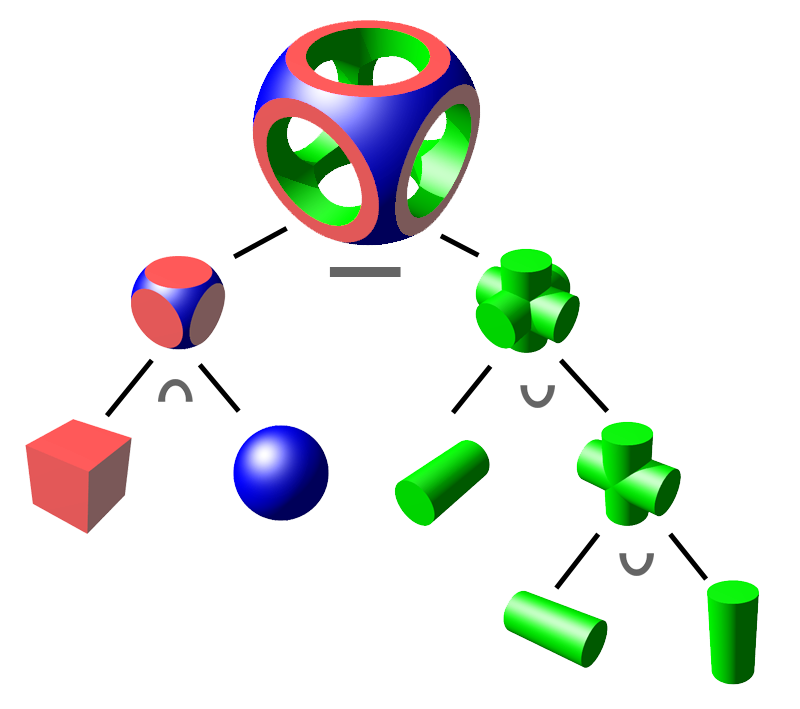
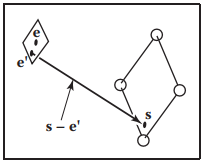
接著,有了CSG構造的模型,那它如何進行相交測試呢?假設有條光纖$\mathbf{a} + t\mathbf{b}$,以及兩個基元圓形$\mathbf{C}$和正方形$\mathbf{S}$。如下圖所示。
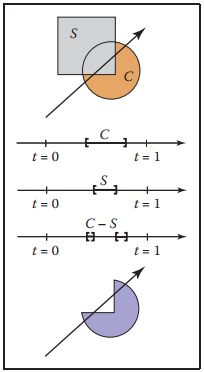
圖中,假設光綫在$t = 0$和$t = 1$之間與圓形相交在$t_0$和$t_1$処,與正方形相交在$t_2$和$t_3$処,這樣,就可以通過判斷$[t_0, t_1]$和$[t_2, t_3]$的位置關係,就能得到光綫與CSG構造模型的相交情況。
在實際應用中,CSG相交測試需要維持一個區間表,也就是光纖與每個基元相交的區間表。另外還需要注意精度問題,特別是同一條光綫對相鄰兩個模型進行測試時,適當設置一定公差間隔,就能保證測試過程的可靠性。
13.4 Distribution Ray Tracing
目前介紹的光綫追蹤獲得的圖片都顯得太“生硬”了,比如陰影,要麽存在要麽不存在;任何物體都是在焦點上成像的等。這樣的表現和現實中往往是不一樣的。現實中,比如陰影,它從存在到不存在是有一個漸變的區域的;而場景中的物體也不可能都在焦點上成像。這些現實中的成像效果,我們可以通過對現有光綫追蹤算法進行簡單的修改就能得到。
13.4.1 Antialiasing
先來説説反走樣問題,原始光綫追蹤在進行相交測試時,只會得到相交或不相交的結果,這就導致渲染結果存在鋸齒現象。如下圖。
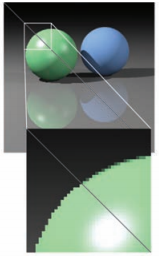
而我們在之前反走樣中提到一個解決方法:獲得目標點周圍一小個區域的結果求平均。例如,我們要獲得$[i, i+1] \times [j, j+1]$點的渲染結果,原來的做法如下。
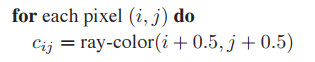
現在,我們在這個範圍内采樣$n \times n$個點,如下圖所示,然後將這些采樣結果求平均作爲結果輸出。
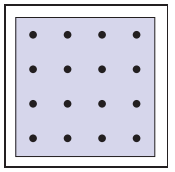
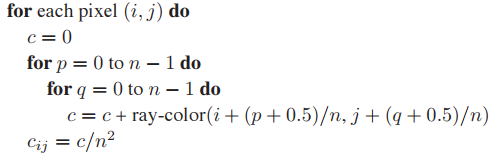
這種規則的采樣方式稱爲regular sampling,這種采樣雖然解決了鋸齒問題,但是又引入了走樣的另一個問題——摩爾紋。爲了解決摩爾紋,我們將這些采樣點隨機分配。如下圖。
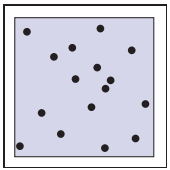
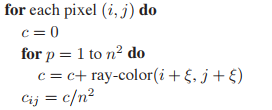
代碼中的$\xi$是取值在$[0,1)$區間内均匀分佈的隨機數。但是這種方式依然會存在聚集現象,因此我們將regular sampling和random sampling結合使用,也就是在$n \times n$的小格中采用隨機采樣。如下圖。
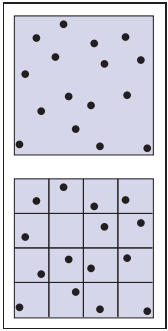
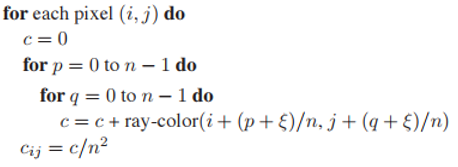
這種采樣方式稱爲stratified sampling(分層采樣)。
13.4.2 Soft Shadows
現在來説説“軟、硬陰影”,就目前光纖追蹤獲得的陰影均爲硬陰影。造成這種現象的原因在於,我們使用的光源都默認為點光源,這就導致了結果只能是可見或不可見兩種結果。而現實中,點光源是很少的,基本都可以認爲是面光源,因此我們可以看下圖中面光源形成的陰影。
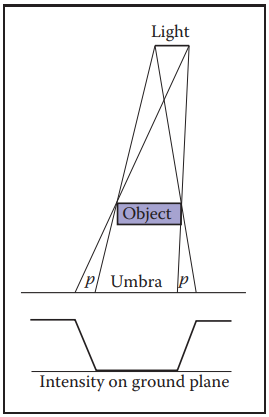
其中,光綫完全到達不到的區域稱爲umbra(本影),光綫可部分到達的地方稱爲penumbra(半影),光綫可以完全到達的地方稱爲anti-umbra(非陰影)。從上圖中可以看出,半影區的光綫强度是漸變的,這就是產生現實中"軟陰影“的原因。
那麽問題來了,要產生”軟陰影“,我們要采用面光源;而我們目前所有的光纖追蹤方法都是基於點光源的,如何解決?很簡單,只要將面光源離散成$N$個點光源,就能解決這個問題了。如下圖左側所示。
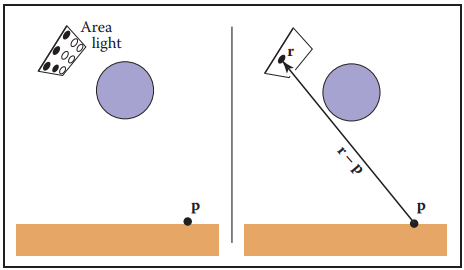
這種做法依然存在兩個問題:一個是計算開銷隨著光源離散程度的增加而增加;另一個是,這種方式在半影區域内依然存在明顯的分界。
為解決這兩個問題,我們將分佈式光綫追蹤生產陰影的方式做一些改變。首先,不再將面光源離散成均匀的$N$個點光源,而是在面光源上隨機采樣$N$個點;另外,在計算陰影位置$\mathbf{p}$処也增加一定的擾動。如上圖中右側所示。
假設上圖中,面光源是一個平行四邊形,它由一個角點$\mathbf{c}$和兩個邊向量$\mathbf{a}$和$\mathbf{b}$構成,那麽該面光源上任意點可以按如下方式表示。
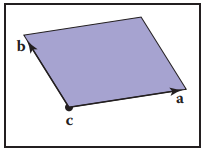
那麽面光源上隨機點只要讓$\xi_1$和$\xi_2$取$[0,1)$均匀分佈的隨機數即可。但是,直接使用隨機數也不是很高效,再加上光源上的采樣位置和渲染位置沒有聯係,那一個好方法就是利用混洗算法生成兩個獨立的$n^2$個擾動集合。實現僞代碼如下。

代碼中的數組$r[]$和$s[]$分別表示渲染位置擾動和光源采樣位置,并且需要刪除所有$r$與$s$一致的情況。這樣就用混洗器替代了隨機數生成器。
一種最簡單的混洗方式如下。
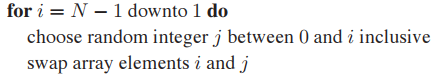
13.4.3 Depth of Field
柔焦現象就是由於我們將小孔成像模型替換爲非零尺寸透鏡成像模型,這就導致清晰像會在焦点前後一定範圍内出現,這個範圍就稱爲景深(Depth of Field)。使所有物體聚焦的平面稱爲焦平面(focus plane)。如下圖所示。
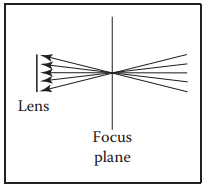
爲了獲得柔焦效果,我們采用的方式與之前處理陰影的方式類似。只是將采樣物體從光源替換爲透鏡。這裏仍然采用正方形透鏡,它產生的效果與現實中圓形透鏡產生的效果類似,如下圖:透鏡上位置進行隨機采樣,觀測位置也同樣進行擾動,并且利用混洗程序避免觀測位置與采樣位置相關聯。這樣就能得到柔焦效果的圖片。
13.4.4 Glossy Reflection
目前爲止,我們談論了鏡面反射和漫反射,但是還有一種反射是介於這兩者之間的,例如抛光的金屬表面。在古代人們用銅鏡來黨鏡子,從銅鏡中可以很好的看到反射物體,但是物體存在一定模糊。這種反射我們稱爲Glossy Reflection。我們可以通過隨機擾動理想反射光綫來模擬該現象。例如下圖所示。
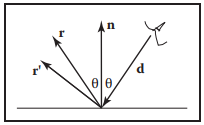
圖中,$\mathbf{r’}$為擾動后的反射光綫,$\mathbf{r}$為理想反射光綫。那麽如何求得$\mathbf{r’}$呢?一個簡單的做法如下。定義一個邊長為$a$的采樣正方形,其垂直于向量$\mathbf{r}$,即反射光綫,令采樣正方形朝向$\mathbf{w} = \mathbf{r}$,且起點位置位於采樣正方形中心,則在采樣正方形上隨機點$\mathbf{p}(u,v)$可以表示爲
這樣,擾動后的$\mathbf{r’}$可表示爲: $$ \mathbf{r}’ = \mathbf{r} + u \mathbf{u} + v \mathbf{v} $$
計算模型如下所示。
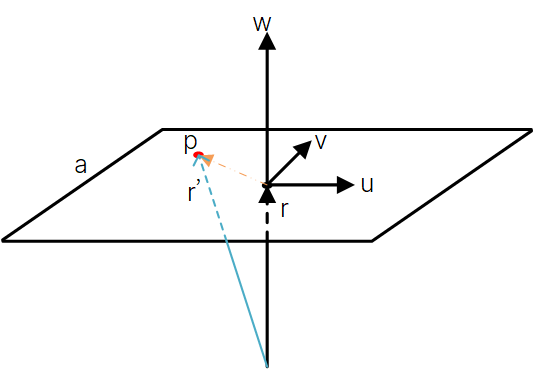
注意,這裏$\mathbf{r’}$不是單位向量,可以根據代碼需要自行進行歸一化操作。
13.4.5 Motion Blur
運動模糊,這個現象由於儅光圈打開的這段時間内,物體運動速度過快而產生的。我們同樣可以模擬這個現象,假設光圈開啓時間為$T_0 \rightarrow T_1$,這個間隔$T$中,某個球體中心從$c_0$移動到了$c_1$,我們對每條觀測光纖設置一個隨機時間$T$,則: $$ T = T_0 + \xi(T_1 - T_0) $$
這樣,每個時刻,球體會在不同的位置,都會有一條對應時刻的觀測光纖與其進行相交測試。這樣就能得到最終運動模糊的圖像。需要注意的是,對於運動物體的包圍盒應該包圍住整個運動軌跡的物體。
Frequently Asked Questions

聲明
該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101:现代计算机图形学入门》時整理的閲讀筆記,文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤,歡迎討論指正:uninitmatrix@gmail.com。