本章節介紹測量光綫的一個工具 —— Radiometry，該工具對於計算機圖形學來説非常重要。本章節還包含Photometry，它用於量化Radiometry，並通過縮放來估計有多少“有用”的光綫。

18.1 Radiometry

本節有許多術語與概念，無論從英文還是中文翻譯上看這些術語都很容易搞混。本節中使用的單位均爲國際標準單位，例如meter(m)和gram(g)。另外説明，本章節内容與原書框架一樣，但會補充Games101課程上提到的一些概念。

18.1.1 Photons - 光子

大家都知道，光具有波粒二象性，在這裏，我們將光纖看著由許許多多的光子組成的。爲了便於理解，本章節中的光子都是指具有一定位置和傳播方向的粒子，波長為$\lambda$，波長單位為$[nm]$，有時也用$[\dot{A}]埃$表示，$1nm = 10 \dot{A}$。

光子的速度$c$通常與其所在的傳播介質有關，無論是波長$\lambda$還是速度$c$，都受到傳播介質的影響，因此定義頻率$f = c/\lambda$用於表徵光子的特性，頻率$f$不受傳播介質影響。另一個不受影響的量就是光子所携帶的能量$q$，其計算方式如下： $$ q = hf = h\frac{c}{\lambda} $$

其中，$h = 6.63 \times 10^{-34} J s$為Plank常數，單位為焦耳秒。

18.1.2 Spectral Energy - 光譜能量

假設我們獲取到大量的光子，那麽這些光子構成的總能量為：

$$ Q = \sum_{i}{q_i} $$

從光的波動性角度會問：“能量在各個波長上的分佈是怎樣的？”對這個問題，可以采用直方圖統計的方式進行，將波長範圍按特定區間長度劃分爲多個bin，然後分別統計每個bin中光子的總能即可。另一個更加常用的方式是，將統計出的總能量除以區間大小，我們將該方式計算結果稱爲光譜能量，用$Q_{\lambda}$表示。

$$ Q_{\lambda} = \frac{\Delta{q}}{\Delta{\lambda}} $$

注意，在圖形學中很少使用$Q$，一直都是使用$Q_{\lambda}$，因此在之後提到的能量均指光譜能量$Q_{\lambda}$；但是在Games101課中，并未使用光譜能量這一概念，所以本節會把兩者都列出。

18.1.3 Power - 功率

功率的定義是單位時間内產生的能量。在圖形學中的功率也一樣，表示光源產生能量的速率，單位為瓦特$[W]$或焦耳每秒$[J\cdot s^{-1}]$表示。 $$ P = \frac{\Delta{q}}{\Delta{t}} $$

相比于傳統功率，在圖形學中更關心的是spectral power（光譜功率），其單位為$[W(nm)^{-1}]$，計算方式如下： $$ \mathcal{\Phi}_{\lambda} = \frac{\Delta{q}}{\Delta{t}\Delta{\lambda}} $$

圖形學中也經常不使用下標$\lambda$表示。

18.1.4 Solid angle - 立體角

我們知道，在圓中，角度和弧長、半徑的關係是： $$ \theta = \frac{l}{r} $$

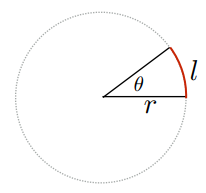
而在球體中，可定義立體角爲所對面積與球體半徑平方的比值： $$ \Omega = \frac{A}{r^2} $$

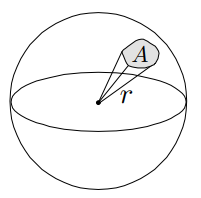
18.1.5 Differential Solid Angle - 微分立體角

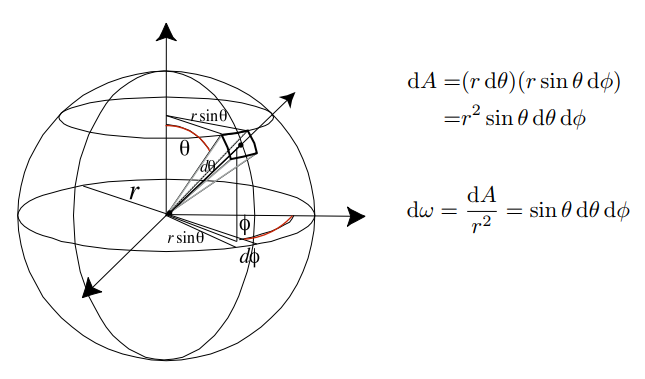
18.1.6 Radiant Intensity - 輻射强度

根據Wikipedia定義，Radiant Intensity為單位立體角内的輻射功率（這裏指的非光譜功率），單位為$[\frac{W}{sr}]$或$[\frac{lm}{sr} = cd = candela]$ $$ I(\omega) = \frac{\Delta P}{\Delta \omega} $$

18.1.7 Spectral Intensity - 光譜强度

根據Wikipedia定義，Spectral Intensity為每單位頻率或波長的Radiant Intensity，單位爲$[W\cdot sr^{-1}\cdot Hz^{-1}]$。計算方式：

$$ I_{\lambda}(\omega) = \frac{I(\omega)}{\Delta \lambda} = \frac{\Delta P}{\Delta \lambda\cdot \Delta \omega} \\[3ex] \text{或}\\[2ex] I_{\lambda}(\omega) = \frac{I(\omega)}{\Delta f} = \frac{\Delta P}{\Delta \lambda \cdot \Delta f} $$

18.1.8 Irradiance - 輻射照度

這個物理量用於描述“在某一點上會有多少光纖到達？”很明顯，回答這個問題一般會使用密度函數。這就推出了Irradiance的定義：單位面積上的Radiant Power。單位為$[W\cdot m^{-2}]$。計算方式為： $$ H = \frac{\Delta P}{\Delta A} $$

18.1.9 Spectral Irradiance - 光譜輻射照度

與之前光譜强度定義類似，Spectral Irradiance的定義為每單位頻率或波長的Irradiance，單位為$[W\cdot m^{-2} \cdot Hz^{-1}]$或$[W\cdot m^{-2}\cdot nm^{-1}]$。計算方式：

$$ H_{\lambda} = \frac{H}{\Delta \lambda} = \frac{\Delta P}{\Delta A\cdot \Delta \lambda} = \frac{\Delta \Phi_{\lambda}}{\Delta A} \\[3ex] \text{或} \\[2ex] H_{\lambda} = \frac{H}{\Delta f} = \frac{\Delta P}{\Delta A\cdot \Delta f} $$

注意，儅光綫離開物體表面，例如反射，此時這個量我們稱爲Radiant exitance，用符號$E$或$E_{\lambda}$表示，它們物理含義相同。但是，相同點的Irradiance和Radiant exitance的量通常是不一樣的。

18.1.10 Radiance - 輻射率

儘管Irradiance解釋了有多少光綫到達某一點，但是它并未指定光纖是從哪個方向來的，而某個特定方向來的光綫量通常也是我們會關心的，因此有了Radiance的定義。根據Wikipedia的定義，單位立體角單位投影面積的輻射功率。單位為$[W\cdot sr^{-1}\cdot m^{-2}]$。計算方式如下： $$ L = \frac{\Delta H}{\Delta \omega} $$

現實中，我們會采用下面這種裝置進行測量。該裝置由irradiance測量器和張角為$\Delta \sigma$的圓錐形調節器構成。

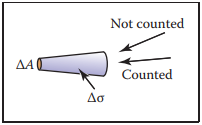
在圖形學中，輻射率是經常計算的量，因爲它不隨空間距離變化。例如下圖，被采樣表面積與距離的平方成正比，到達檢測器的光綫與距離的平方成反比，所以兩個檢測器的讀數是一致的。

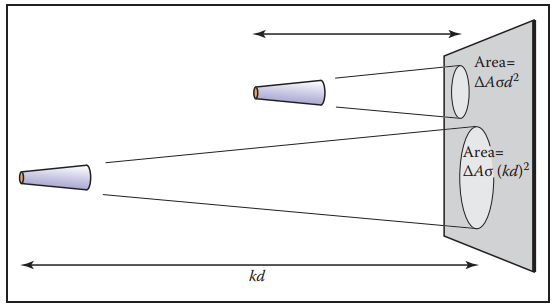
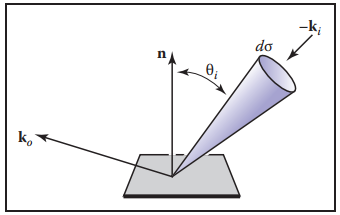
另外，注意定義中的單位投影面積，實際中，檢測器通常與被測表面不會100%成投影關係，之間相差一個校正因子$\cos{\theta}$。如下圖所示。所以在計算輻射率時，要將該校正項加上。

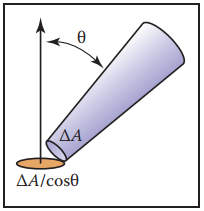
$$ L = \frac{\Delta H}{\Delta \omega \cdot \cos{\theta}} $$

最後注意，在使用過程中，我們通常會將離開某個表面的輻射率稱爲surface radiance(表面輻射率)，用$L_s$表示。把某個表面的輸入輻射率稱爲field radiance(場輻射率)，用$L_f$表示。

$$ L_s = \frac{\Delta E}{\Delta \omega \cos{\theta}} \\[3ex] L_f = \frac{\Delta H}{\Delta \omega \cos{\theta}} $$

18.1.11 Spectral Radiance - 光譜輻射率

與其他光譜量定義類似，Spectral Radiance定義爲每單位頻率或每單位波長的Radiance。單位爲$[W\cdot sr^{-1}\cdot m^{-2}\cdot Hz^{-1}]$或$[W\cdot sr^{-1}\cdot m^{-2}\cdot nm^{-1}]$。計算方式： $$ L_{\lambda} = \frac{L}{\Delta \lambda} \
L_{v} = \frac{L}{\Delta v} $$

注意，這裏用$v$表示頻率，否則會與場輻射率表示混淆。

至此，輻射度量學的一些基本量就介紹完畢，下面是這些量的總結。

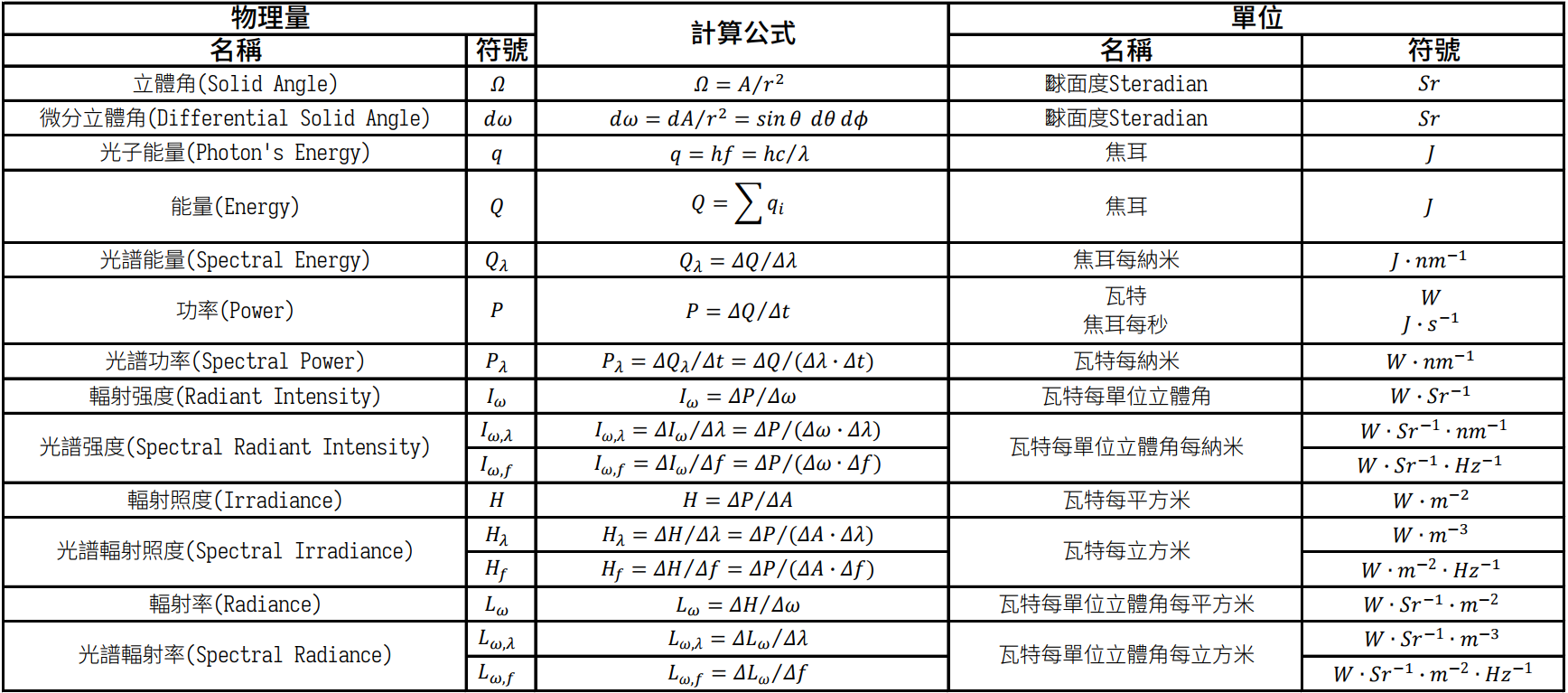
再放一張Radiant Intensity、Irradiance和Radiance的對比圖，一開始這三個量太容易搞混了。

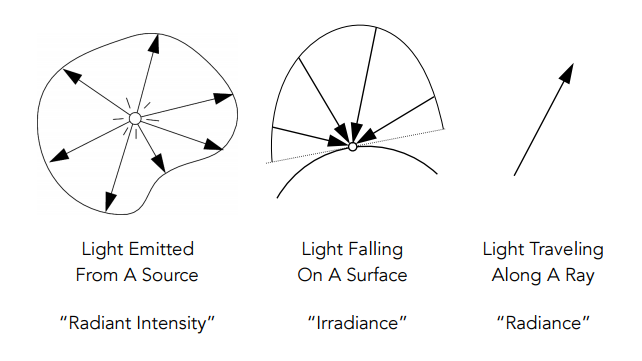
18.1.12 Radiance and Other Radiometric Quantities

假設已知表面的field radiance，那麽其他輻射度量學的物理量都能通過該量獲得，這就是爲什麽radiance被認爲是輻射度量學量的基礎。例如，下圖中的irradiance可以通過如下方式計算：

$$ H = \int_{\text{all } k}L_f(k)\cos{\theta}d\sigma $$

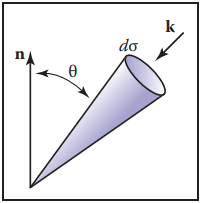
接著上面這個例子，假設從各個方向來的field radiance不變，利用經典球坐標係表示微分立體角$d\sigma$： $$ d\sigma \equiv \sin{\theta}d\theta d\phi $$

那麽，irradiance可表示成：

$$ \begin{align} H &= \int_{\phi = 0}^{2\pi}\int_{\theta = 0}^{\frac{\pi}{2}}L_f \cos{\theta}\sin{\theta}d\theta d\phi \\[2ex] &= \pi L_f \end{align} $$

注意上面結果中的因子$\pi$，這個因子在輻射度量學中會經常出現，并且是我們選擇如何測量立體角的產物。例如，單位球面積的倍數是$\pi$而不是$1$。

同理，我们可以计算某个面上的Power。 $$ \Phi = \int_{\text{all }x}H(x)dAv $$

18.1.13 BRDF

這玩意看全稱Bidirectional Reflectance Distribution Function(雙向反射分佈函數)還挺唬人的，其實就是用一個函數來表徵入射光綫經過物體表面后如何被反射走的，本質上也是表徵了物體表面的特徵。直覺上，假設入射光綫來自某個方向$k_i$，在出射方向$k_o$上會有一個立體角的散射。基於這種現象，我們采用下面方式進行BRDF的測定。

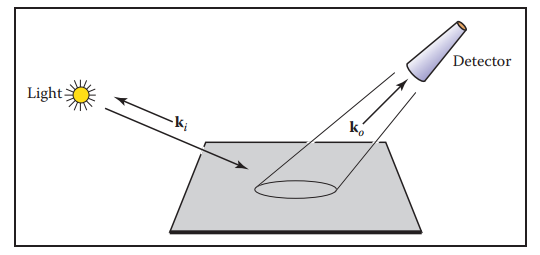
我們將測定的量用比值形式刻畫。其中$H$表示位置$k_i$上的Irradiance，$L_s$表示方向$k_o$上的field radiance。這樣在所有方向對上進行測量后就可以得到一個$4$維函數$\rho(k_i, k_o)$。這個函數就被稱爲BRDF，它刻畫物體表面反射光綫的方向性質。 $$ \rho = \frac{L_s(k_o)}{H(k_i)} $$

Directional Hemispherical Reflectance

有了BRDF后，就會想知道“入射光綫有多少被反射？”顯然這個問題並不好回答，因爲這還和入射光綫的方向分佈有關。但是可以簡化這個問題，我們只考慮某個方向$k_i$上的反射部分，這部分被稱爲directional hemispherical reflectance(半球方向反射係數)，記爲$R(k_i)$。 $$ R(k_i) = \frac{\text{所有出射方向上的功率 }k_o}{\text{方向}k_i\text{上的功率}} $$

假設我們考慮入射功率$\Phi_i$作用在一小塊面積$\Delta A$上，那麽可以將$R(k_i)$轉換爲radiant exitance和irradiance的比值。 $$ R(k_i) = \frac{E(k_o)}{H(k_i)} $$

根據能量守恆，$R(k_i)$​​​取值範圍為$[0,1]$​​​。下面推導$R(k_i)$​​​​與BRDF之間的關係。

根據BRDF的定義： $$ L(k_o) = H(k_i)\rho(k_i, k_o) \tag{18.1} $$

由Radiance的定義， $$ L(k_o) = \frac{\Delta E}{\Delta \sigma_{o} \cos{\theta_o}} \tag{18.2} $$

其中$E$表示在方向$k_o$上某一小區域的radiant exitance。有公式(18.1)和公式(18.2)可知。 $$ H(k_i)\rho(k_i, k_o) = \frac{\Delta E}{\Delta \sigma_{o} \cos{\theta_o}} $$

整理可得： $$ \frac{\Delta E}{H} = \rho(k_i,k_o)\Delta \sigma_{o}\cos{\theta}_o $$

該式表示某個出射方向$k_o$與入射方向$k_i$的irradiance比率關係。根據$R(k_i)$定義，要計算所有出射方向上的功率，所以$R(k_i)$的積分形式如下： $$ R(k_i) = \int_{\text{all }k_o}\rho(k_i,k_o)\cos{\theta_o}d\sigma_o $$

這樣就將BRDF與半球方向反射係數聯係起來了。

Ideal Diffuse BRDF

對於理想的漫反射模型Lambertian，它的BRDF值在每個方向對上都是相同的，因此可以用一個常量表示$\rho = C$，這也意味著在任意觀測方向上，物體表面的radiance是相同的。如果我們計算$R(k_i)$，那麽：

$$ \begin{align} R(k_i) &= \int_{\text{all }k_o}C\cos{\theta_o}d{\sigma_o}\\[2ex] &= \int_{\phi_o=0}^{2\pi}\int_{\theta_o = 0}^{\frac{\pi}{2}}C\cos{\theta_o}\sin{\theta_o}d{\theta_o}d{\phi_o}\\[2ex] &= \pi C \end{align} $$

這個公式中可以看出，對於理想的Lambertian反射表面($R = 1$)，則$\rho = \frac{1}{\pi}$。那麽對於一般的Lambertian表面($R = r$)，其BRDF值為： $$ \rho(k_i, k_o) = \frac{r}{\pi} $$

這個關係也從側面證實了在使用球面坐標系時，縮放因子一般是$\pi$的倍數而不是$1$。

18.2 Transport Equation

根據BRDF定義，它的形式并不直觀，我們可以將其寫成只有radiance項的形式。假設我們能夠獲得某個立體角$\Delta \sigma_i$下的radiance$L_i$，并且能測出$k_o$方向上的反射radiance$L_o$，如下圖所示，那麽我們就能將BRDF寫成如下形式。 $$ \rho = \frac{L_o}{L_i\cos{\theta_i}\Delta{\sigma_i}} $$

重新整理可得一個小部分的radiance形式： $$ \Delta{L_o} = \rho(k_i, k_o)L_i\cos{\theta_i}\Delta{\sigma_i} $$

由於入射光綫可以從任意方向來，所以計算結果需要對所有入射方向光纖進行積分。 $$ L_s(k_o) = \int_{\text{all }k_i} \rho(k_i, k_o)L_f(k_i)\cos{\theta_i}d\sigma_i \tag{18.3} $$

這樣得到的等式在圖形學中稱爲rendering equation(渲染方程)。

等式(18.3)表示從光源來的光綫，但是實際情況下，其他物體表面也有可能會反射出光纖到達觀測點，如下圖所示，觀測點$x$在$k_i$上接收到了從$x'$反射來的光纖，那麽此時這條光纖的$L_f(k_i)$就要表示爲$L_s(-k_i)$，其立體角可用如下方式計算。 $$ \Delta{\sigma_i} = \frac{\Delta{A’}\cos{\theta’}}{||x-x'||^2} $$

其中，$\Delta{A’}$是與$x'$關聯的面積。

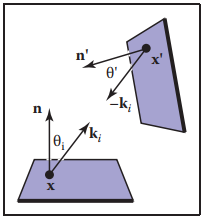
將$\Delta{\sigma’}$帶入公式(18.3)可得：

$$ L_s(x,k_o) = \int_{\text{all }x'\text{ visible to }x}\frac{\rho(k_i,k_o)L_s(x',x-x')\cos{\theta_i}\cos{\theta'}}{||x-x'||^2}dA' \tag{18.4} $$

這裏，我們使用非歸一化向量$x-x'$表示從$x'$到$x$的方向，同樣，我們將$L_s$改寫成關於位置和方向的函數。對於公式(18.4)依然有不足，就是積分域不好確定，因此這裏定義一個指示函數。

$$ v(x, x') = \begin{cases} 1, &\text{if }x\text{ and }x'\text{ are mutually visible},\\ 0 &\text{otherwise.} \end{cases} $$

渲染方程可改寫為 $$ L_s(x, k_o)= \int_{\text{all }x’}\frac{\rho(k_i, k_o)L_s(x’, x-x’)v(x,x’)\cos{\theta_i}\cos{\theta’}}{||x-x'||^2}dA’ \tag{18.5} $$

下面接著這個方程説事。以下内容來自課程Games-101。

公式(18.5)反映了某個觀測點$x$反射了其他所有位置$x'$來的光纖，但是觀測點$x$本身可能也會向外輻射光纖，所以渲染方程的形式可寫爲： $$ L_r(x, k_o) = L_e(x,k_o) + L_s(x, k_o)\tag{18.6} $$

等式(18.6)展开后是第二类Fredholm积分形式（Ps：这是啥？不懂，但不影响后面理解）。在数值计算中，可以将其写成标准化形式： $$ I(u) = E(u) + I(v)K(u,v)dv\tag{18.7} $$

其中$E(u)$就对应$L_e(x, k_o)$项，$I(v)$對應公式(18.5)中的$L_s(x’, x-x’)$項，$K(u,v)dv$對應公式(18.5)中剩餘的積分項$\frac{\rho(k_i, k_o)\cos{\theta_i}\cos{\theta’}}{||x-x'||^2}dA'$。繼續簡化，假設物體自身向外輻射的irradiance相同，那麽上面等式(18.7)可簡化成 $$ L_n = E + KL_{n-1}\tag{18.8} $$

等式(18.8)是個遞歸形式，其中$n$表示了光纖從發光體出發后彈射次數。將這個等式展開可得 $$ L_n = E + KE + K^2E + K^3E + \cdots\tag{18.9} $$

等式(18.9)就是Ray Tracing的本質，其中各項的物理含義如下

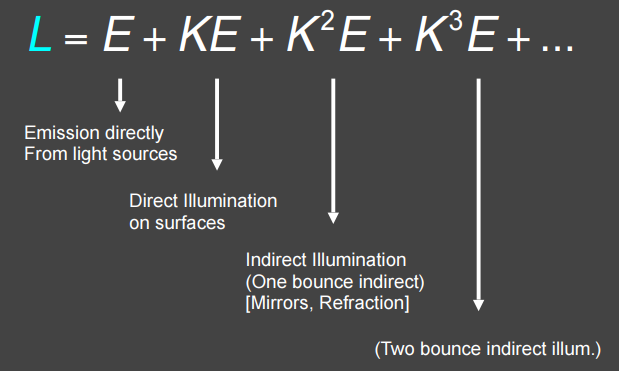
就説妙不妙吧！！！！

18.3 Photometry

對於每一個spectral radiometric quantity(光譜輻射度量量)，都有一個相對應的photometric quantity(光度度量量)來衡量有多少輻射率對人眼有效。假設給定一個光譜輻射度量量$f_r(\lambda)$，相對應的光度度量量$f_p$可表示爲： $$ f_p = 683\frac{lm}{W}\int_{\lambda = 380 nm}^{800nm} \bar{y}(\lambda)f_r(\lambda)d\lambda $$

其中，$\bar{y}$表示人類視覺系統的luminous efficiency function(發光效率函數)。常量$683$是爲了讓定義與歷史上的絕對光度測定量保持一致。

對於人眼來説，函數$\bar{y}(\lambda)$在各個波長上是不同的，如下圖所示。低於$380 \ nm$波長的光是無法被人眼看到的，此時，$\bar{y} = 0$。在波長$\lambda = 555 \ nm$達到峰值，這波長是純綠色的光。之後逐漸降低直到紅外區域邊界$\lambda = 800 \ nm$処。

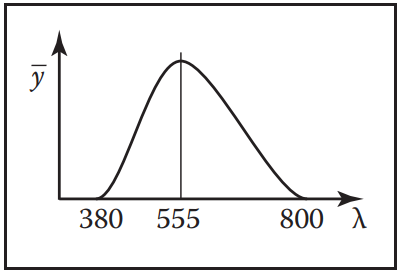
計算機圖形學中最常用的光度測定量是亮度，其光度測定量為 $$ Y = 683 \frac{lm}{W}\int_{\lambda = 380 \ nm}^{800 \ nm}\bar{y}(\lambda)L(\lambda)d\lambda $$

該量表示一個物體有多亮，單位為流明$lm$。而實際使用中，通常要結合所消耗的功率，例如燈泡，燈泡的效率越高，產生的光纖就越多，其$\bar{y}$也越大，從而每瓦特所產生的流明也越多。從而亮度單位就是$\frac{lm}{W}\cdot \frac{W}{(m^2sr)} = \frac{lm}{m^2sr}$，其中每單位立體角内的流明量被定義爲candela(坎德拉, cd)，因此亮度單位通常采用$\frac{cd}{m^2}$。

Frequently Asked Questions

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。