本節介紹圖形學中最基本的，最常用的幾種數據結構：網格結構(mesh structures)，空間數據結構(spatial data structures)，場景圖(scene graphs)和平鋪多維數組(tiled multidimensional arrays)。

網格結構中將介紹“翼邊”結構(the winged-edge data structure)和“半邊”結構(the half-edge structure)。這兩種結構在管理模型時非常有效，特別是在模型簡化或細分時；場景圖主要用於管理場景中物體閒的關係與變換等；對於空間數據結構，主要介紹三種管理空間物體的方法——BVH、層級空間細分和均匀空間細分；最後平鋪多維數組介紹如何提高内存訪問效率。

12.1 Triangle Meshes

大多數真實模型都可以用一系列複雜的、共享頂點的三角形表示，這就稱爲三角形網格(triangular meshes)，這些網格的處理效率對程序效率影響至關重要，因爲這些網格數據存儲在硬盤或送到内存中使用，CPU將這些數據傳送到圖形程序中時，需要占用大量帶寬，因此我們希望最小化它們的占用空間；另外，訪問某個網格鄰近網格有時也非常重要。本節將介紹如何解決這些基本的關鍵性問題。

12.1.1 Mesh Topology

網格拓撲，這裏先講兩個概念：流形(manifold)和非流形(non-manifold)。這兩者如何區分：假設網格中有三個三角形共享一條邊，在這條共享邊上任取一點，在該點某個很小的領域内若存在任意一點，它所歸屬的網格有歧義，則稱爲非流形結構；反之為流形結構。如下圖所示。

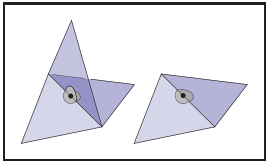
類似的，如果三角形共享一個頂點，如下圖左圖所示，如果想將該網格結構以共享頂點爲中心鋪平，該共享頂點領域内的點所屬網格存在歧義，因此它并不屬於流形結構；而右圖中的網格不存在這個問題，所以它屬於流形結構。

圖形學中多少算法都是假設網格為流形的，在處理流形網格時，我們有很好的屬性判斷來避免“死循環”和意外崩潰。判斷條件歸結爲檢查所有的邊是否是流形的和判斷所有的點是否是流形的（下面以三角形網格爲例説明）：

  • 每條共享邊只有兩個三角形共享；
  • 每個頂點周圍都有一個完整的三角形循環；

這兩個判斷條件約束過於強，在處理邊界時顯然無法滿足判斷條件，因此，爲了兼容邊界處理，我們將上述兩個條件適當“放鬆”：

  • 每條邊至多只屬於兩個三角形；
  • 每個頂點周圍只有一組邊界相鄰的三角形；

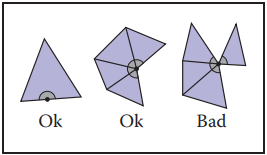
下圖展示了放鬆條件后的流形判斷結果。

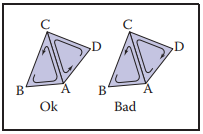
最後，拓撲結構中還有一個問題，如何區分表面(outside)和裏面(inside)，區分表裏是爲了定義表面的方向。通常對於三角形，我們將頂點逆時針排列的一面定義為表面，如下圖所示。這樣，一個網格結構就能確定它的表面——當且僅當相鄰的三角形有一致的方向時。

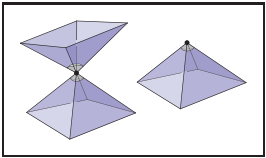
對於非流形無法唯一確定方向，對於帶有邊界的有效流形甚至就是流形的網格，也沒有統一的方式來定向三角形，最好的例子就是莫比烏斯環。但這種情況在應用中很少出現。

12.1.2 Indexed Mesh Storage

三角形網格最直接的存儲方式就是頂點存儲，將每個三角形按頂點獨立存儲。存儲結構如下。

下圖所示是一個簡單的三角形網格。

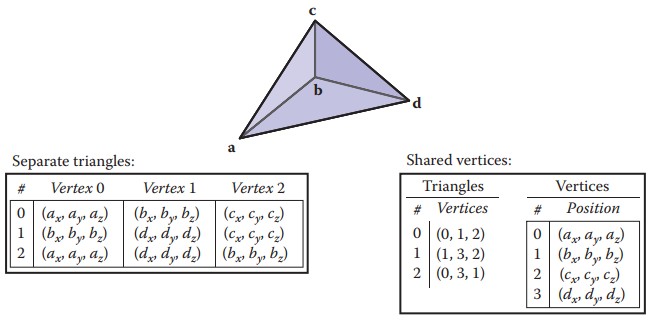
這種存儲方式導致，點$\mathbf{b}$被存儲了三次，剩餘點被存儲了兩次。存儲結構如下。

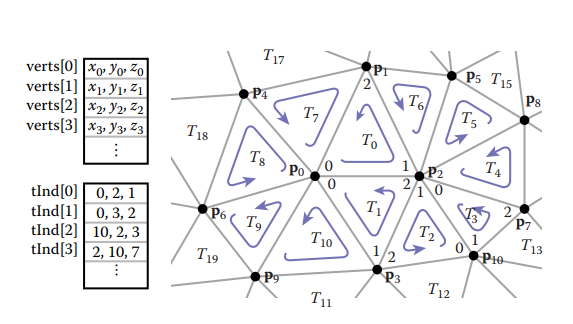
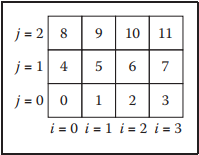
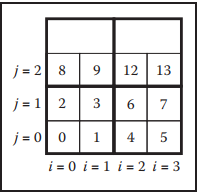
通過修改存儲方式，我們可以讓冗餘數據減少，例如，只保存四個頂點數據，每個三角形用頂點序號表示。存儲結構如下。這種方式存儲稱爲shared-vertex mesh。

数据结构中，nv表示顶点总数，nt表示三角形总数。下图是使用shared vertex方法存储数据的展示。

我们来比较下这两种存储方式存储大小是多少。假设，$n_v$为顶点数，$n_t$为三角形数，基本数据类型为32-bit浮点和32-bit整型，那麽空間占用計算如下：

  • 對於完整三角形存儲：每個三角形有三個頂點，每個頂點有$(x, y,z)$三個坐標值，所以縂存儲占用$9n_t$；
  • 對於共享頂點式存儲：頂點存儲為$3n_v$，三角形索引存儲為$3n_t$，總計$3n_v + 3n_t$。

從上面兩種方式計算結果可以看出，存儲量與$n_t$和$n_v$的比值相關。根據經驗來説，通常情況下，一個頂點大約會連接六個三角形（當然這不是絕對的，只是經驗而已）。又因爲三角形連接三個頂點，這意味著$n_t$和$n_v$近視滿足$n_t \approx 2n_v$的關係。因此完整三角形存儲空間大約爲$18n_v$，共享頂點式存儲大約為$9n_v$，使用共享頂點可以將存儲減少一半，這在大多數應用中都是適用的。

TIPS: 有些人可能會認爲只有2倍的因子不足夠誘惑，但是如果加上每個頂點的屬性時，這個因子就會產生相當可觀的影響。

12.1.3 Triangle Strips and Fans

雖然共享頂點方式的存儲方式能夠壓縮存儲空間，但其依然存在冗餘信息（存儲每個三角形頂點編號時）。爲了進一步減少冗餘信息，triangle strips和triangle fans這兩種方式被采用。下圖中，左側為triangle strips，右側為triangle fans。

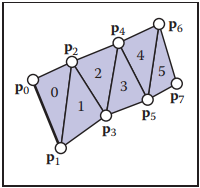
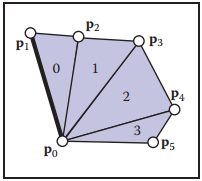
對於fans結構，上圖中三角形的編號表示為$[(p_0, p_1,p_2), (p_0, p_2, p_3), (p_0, p_3, p_4), (p_0, p_4, p_5)]$，所有三角形都共享一個頂點$p_0$，并且另外兩個頂點的序號是相鄰的，例如$1-2$、$2-3$ …因此我們可以將三角形編號存儲爲$[0, 1,2,3,4,5]$，這樣就將冗餘信息剔除，進一步減少了存儲空間。

對於strips結構，剔除冗餘的方式與fans結構類似。上圖右側圖中，三角形可表示爲$[(p_0, p_1, p_2), (p_2, p_1, p_3), (p_2, p_3, p4), (p_4, p_3, p_5), (p_6, p_5, p_7)]$，假設頂點序按照$[0,1,2,3,4,5,6,7]$方式存放，那麽strips結構取三角形的方式為：取當前序號左右相鄰序號構成一個三角形以及當前序號與其後兩個序號構成下一個相鄰三角形，之後將當前序號向後移動兩位重複之前的取法。下圖就是strips結構表示的更大的網格結構。

無論是fans結構還是strips結構，$n+2$個頂點足以描述$n$個三角形，這要比標準$3n$個頂點的描述節省的不少空間。另外，對於strips結構，假設其長度趨於無窮大時，其使用的空間約爲標準存儲空間的$\frac{1}{3}$。基於strips結構這種快速降低空間使用率的特性，實際中，經常使用“貪心”算法將一些非結構的網格組成一些短的strips結構使用。

12.1.4 Data Structures for Mesh Connectivity

對於前面介紹的幾種數據結構都只能靜態的表示，對於動態處理和網格編輯依然無法滿足，因此我們需要進一步完善數據結構。在進行這一步前，我們需要先考慮下面幾個問題：

  • 假設給定一個三角形，它相鄰的三個三角形是哪些？
  • 假定給定一條邊，哪兩個三角形共享此邊？
  • 給定一個頂點，哪些面共享該頂點？
  • 給定一個頂點，哪些邊共享該頂點？

根據這幾個問題，最直觀的解決方案就是定義Vertext，Edge和Triangle三種結構，在三種結構内部記錄與它相關的其他數據。

一個好的網格結構能在常數時間内進行鄰域查詢，所謂常數時間就是鄰域查詢所消耗的時間與網格大小無關，下面將介紹三種網格結構。

The Triangle-Neighbor Structure

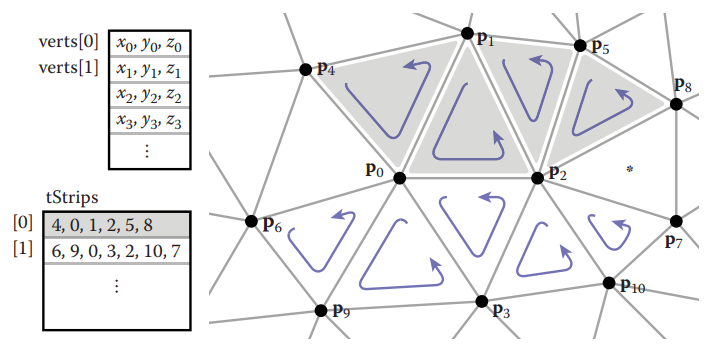
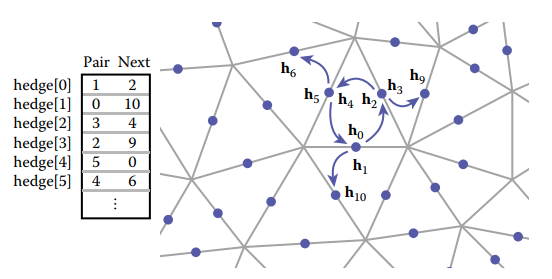
基於共享頂點的三角形網格我們可以創建一個緊凑型的網格結構：利用指針，在每個三角形結構中記錄與其鄰接的三個三角形；在每個頂點中，記錄共享該頂點的任意一個三角形。如下圖所示。

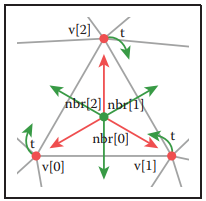
對於結構中Triangle.nbr，它的第$k$個鄰接三角形共享第$k$和$k+1$號頂點。因此這種結構被稱爲triangle-neighbor結構。

基於這種結構，整個網格結構可以用如下結構體記錄。相比于標準的索引式三角形網格結構，該結構多了兩個數組：一個記錄每個三角形相鄰的三個三角形；一個記錄每個頂點鄰接的任意一個三角形。

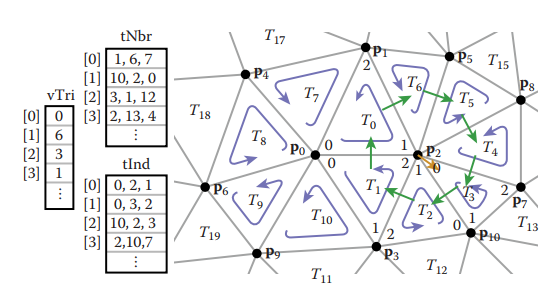
利用這種結構，很容易從一個頂點出發，在常數時間内遍歷共享該頂點的所有三角形。因爲，假設共享頂點$v$是三角形$t$的第$k$個頂點，那麽$t.nbr[k]$是該共享頂點順時針方向上的下一個三角形。這樣遍歷算法如下：

上圖中程序顯然可以完成任務，但是依然不夠完美——在循環内部需要一直判斷共享頂點在當前三角形中的序號。爲解決這個問題，我們修改數據結構，將原先三角形存儲相鄰三個三角形的指針，改爲存儲這些三角形特定邊的指針。如下圖所示。

新的數據結構中添加了Edge結構，因爲一條邊由兩個三角形共享，所以Edge.t可以記錄兩個三角形中的任意一個，Edge.i記錄了當前這條邊在Edge.t三角形中是第幾條邊。這樣我們就可以通過簡單的測試來判斷，遍歷過程是否回到了起點。 $$ t.{\rm nbr}(j).{\rm t.nbr}(t.{\rm nbr}[j].{\rm i}).{\rm t} == t $$

這個等式有點繞，但是可以拆分開看：首先是$t.{\rm nbr}(j).{\rm t}$，表示在三角形$t$中序號為$j$的邊所屬的三角形；第二部分$t.{\rm nbr}[j].{\rm i}$，表示共享邊$j$在另一個三角形中的序號；最後整個等式可以理解爲，與當前三角形$t$共享$j$號邊的另一個三角形是否與初始三角形相等。那麽這個算法按下面方式運行。（PS：原書中的代碼存在bug，無法處理初始條件，應改爲如下形式才能正常運行）

1
2
3
4
5
6
7

TriangleOfVertex(v){
	{t, i} = v.e;
	do{
		i = (i+1) mod 3;
		{t, i} = t.nbr[i];
	} while (t != v.e.t);
}

這裏與原書代碼的區別在於，${\rm i = (i+1) \ mod \ 3}$的位置，如果放在之後做，相當於只取到初始三角形，循環只進行一次就結束了。

抛開細節，這段代碼要比之前判斷頂點的方式簡潔的多。而在存儲空間方面，該結構所用存儲大約為$4n_v + 6n_t \approx 16n_v$。當然，該結構也存在一些缺陷，它的終止條件是返回到起始的三角形，但是，儅在邊界時，這個終止條件無法自然的滿足。爲了彌補這一不足，我們可以為邊界上的三角形設置一個$flag$值，例如$-1$，謹慎處理就能推廣到有邊界的流形網格中。

The Winged-Edge Structure - 翼邊結構

winged-edge結構是將前面以三角形面爲主導的方式，改爲以邊為主導。該結構在存儲網格連接信息方面得到廣汎應用。下圖展示了winged-edge結構代碼。

winged-edge結構中的邊，存儲了邊的兩個頂點、逆時針方向上下一條邊和上一條邊的指針（分左右兩側），以及共享該邊的兩個三角形面。頂點和面結構中存儲了它們連接任意一條邊的指針。下圖中説明winged-edge結構的左右方向判定（逆時針方向為主方向）。

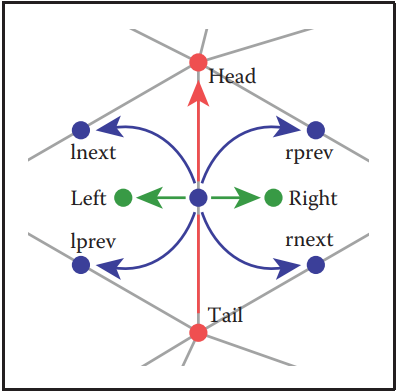
下圖展示以winged-edge結構存儲網格結構的結果。

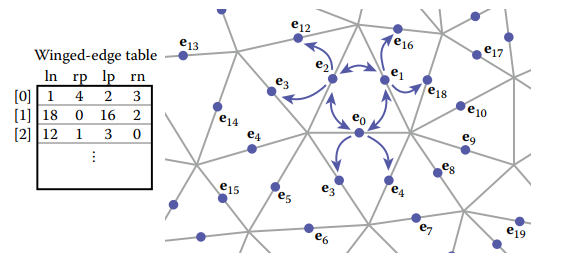
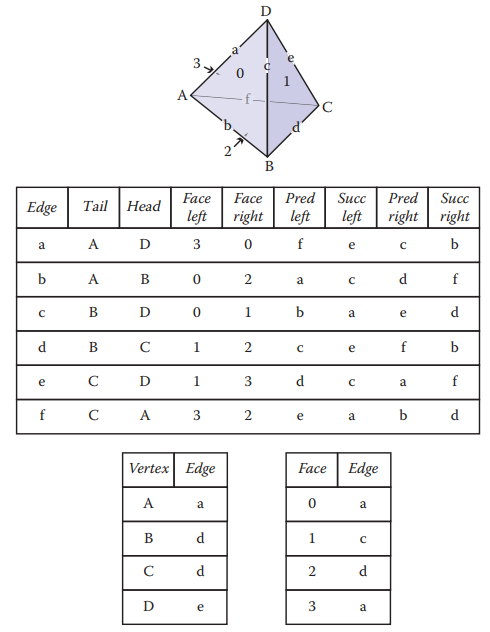
winged-edge結構能夠從某個頂點或面出發，在常數時間内訪問與之相關的所有邊，同樣也能獲得相鄰的頂點或面的信息。



除了上面所説的優勢外，winged-edge結構可以適用於任意多邊形而不僅僅是三角形網格。另外，該結構還能在時間和空間中繼續進行取捨，例如，將邊結構中的雙向鏈表改爲單向鏈表（刪除prev節點），那麽就能節約空間，而要花更多的時間來定位上一個（或下一個）節點。

The Half-Edge Structure - 半邊結構

前面説的翼邊結構已經非常優雅了，但依然不夠（再次驗證了人類是貪婪的）。從翼邊結構的遍歷代碼中可以看出，每次移動都要判斷移動方向，這個判斷量是巨大。爲了解決這個問題，我們將翼邊結構中的一條邊拆分成兩個半邊，這就是爲什麽該結構稱爲half-edge的原因。

在half-edge結構中，共享該邊的兩個三角形各自分得一個半邊，半邊的方向與所屬三角形方向一致，但兩個半邊方向相反。如下圖所示。

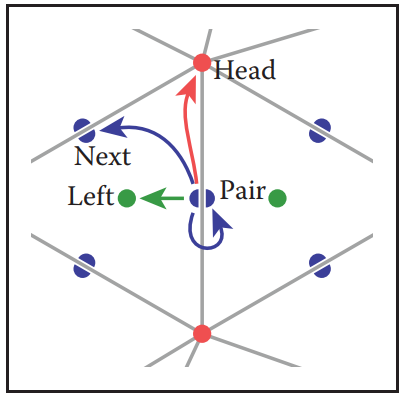
half-edge數據結構如下。

與winged-edge結構遍歷方式類似，但half-edge結構不用每次確定移動方向，只需移動到與當前半邊配對的另一半邊結構即可繼續。



(PS: 這裏通過頂點遍歷相關邊緣的代碼與原書中的不同，原書中的代碼是錯誤的，會導致死循環！)

利用half-edge結構存儲及通過面遍歷相關邊的結果如下。

上面提到的三種網格拓撲結構，除了遍歷操作外，對於邊交換、頂點塌縮、頂點拆分、三角形面增減等操作同樣能有效支持。

12.2 Scene Graphs

上一節介紹的網格拓撲結構是針對單個物體的，而在一個場景中存在許多物體，這些物體如何擺放在正確位置，這又是另一個廣汎存在的問題。在複雜場景中，如果能有效的管理每個物體的變換矩陣，那麽對於場景的操作是十分方便的。許多場景管理采用"分級式"管理，這就是所謂的scene graph（場景圖）。

本節利用下圖中所示的鉸鏈杆結構説明場景圖如何運作。

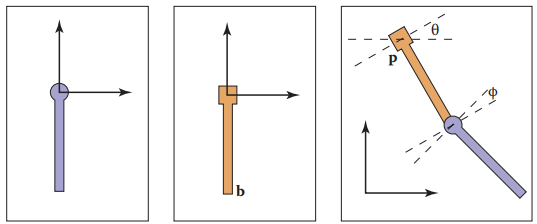
上圖中，左側兩個部件為鉸鏈杆的兩個部件，它們有自己的坐標系，稱爲局部坐標系，假設兩個鉸鏈杆要形成右側圖中的結構，那麽可以按以下方式進行：首先，先將兩個鉸鏈杆在局部坐標系下進行旋轉操作；再將局部坐標系變換到世界坐標系中進行平移操作。

這個過程用矩陣表示為：對於藍色鉸鏈杠：

對於黃色鉸鏈杆略微複雜，但是基本思路不變：先旋轉，再平移，最後與藍色鉸鏈杆變換矩陣合并。

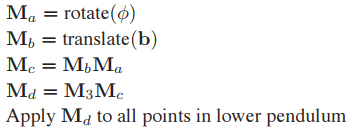
從這個過程可以發現，黃色鉸鏈杆除了依賴自身旋轉變換外，還依賴藍色鉸鏈杆的變換。因此，它們的層級結構如下圖所示，依賴關係自上而下。

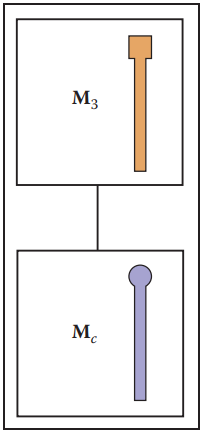
下面在舉個複雜的例子，一艘輪船上放置了一輛車，而且這輛車可以在輪船甲板上運動。那麽它們閒的層級關係如下圖所示。

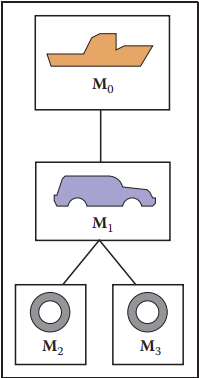
  • 輪船變換矩陣：$\mathbf{M}_0$；
  • 車身變換矩陣：$\mathbf{M}_0\mathbf{M}_1$;
  • 車的左輪變換矩陣：$\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2$;
  • 車的右輪變換矩陣：$\mathbf{M}_0\mathbf{M}_1\mathbf{M}_3$.

存儲這種層級矩陣最有效的數據結構就是"堆棧"(stack)，這樣，只需將所有部件的變換矩陣按層級關係入棧，需要時按順序出棧，就能得到最終需要的變換矩陣。例如，對於上面輪船的例子中的左輪。依次入棧為：

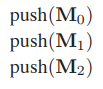
那麽，獲得左輪變換矩陣$\mathbf{M}$可以依次出棧得：$\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2$。按照這種思路，我們可以給出遞歸遍歷獲取場景圖中某個部件變換矩陣的算法：

當然，場景圖不可能只有這種方式，但是基本思路都是一樣的。

12.3 Spatial Data Structures

物體在場景中如何擺放確定後，接下來就是如何在場景中快速定位物體，例如，在光綫追蹤應用中，需要快速定位與光纖相交的物體；在交互式設計時需要在任意視點下確定哪些物體可見等等。這些應用都需要各種空間數據結構來支撐。本節就來討論空間數據結構spatial data structures。

本節以光纖追蹤應用為驅動，主要介紹三種技術：

  • bounding volume hierarchies - BVH
  • uniform spatial subdivision
  • binary space partitioning

12.3.1 Bounding Boxes

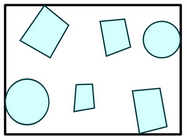
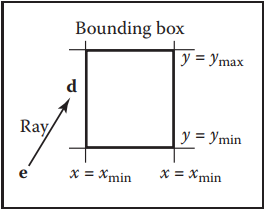
這裏需要先説明一個概念——bounding box，所謂bounding box就是包圍$N$個物體的最小矩形框，如下圖所示。

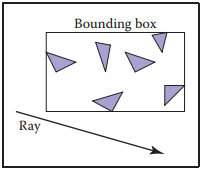
下面介紹在2D空間中，如何判斷光纖與bounding box的關係的，值得注意的是，我們其實只需要知道光纖是否與bounding box相交，而不需要知道具體交點在哪裏。

假設，bounding box用區間表示 $$ (x,y) \in [x_{min}, x_{max}] \times [y_{min}, y_{max}] $$

光纖定義爲： $$ \mathbf{p} = \mathbf{e} + t\mathbf{d} $$

將其拆分到$x$和$y$方向可得：

$$ x_p = x_e + tx_d \\ y_p = y_e + ty_d $$

假設光纖穿過$x = x_{min}$，那麽： $$ t_{xmin} = \frac{x_{min} - x_e}{x_d} $$

這樣可以計算出光纖與bounding box四條邊的$t$值，我們只需要判斷這四個$t$值閒的關係可知光纖是否與bounding box相交。

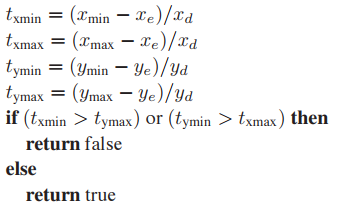
對比下圖可以發現其中的規律，簡而言之就是，區間$[t_{xmin}, t_{xmax}]$和區間$[t_{ymin}, t_{ymax}]$有重叠時，光纖與bounding box相交。儘管邏輯簡單，但其中還存在一些細節問題。

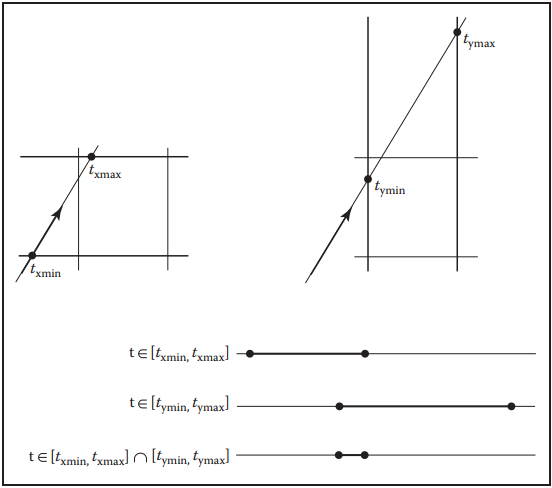
首先，我們先討論假設$x_d < 0$的情況（$y_d$情況類似）。這種情況下，光纖會先交於$x_{max}$再交於$x_{min}$，那麽計算方式要變爲如下形式。

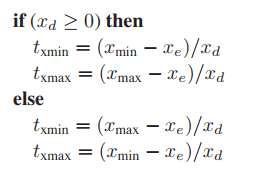
接著，儅$x_d = 0$或$y_d = 0$時，也就是光纖是沿豎直或水平方向時，上面提到的方法就會遇到除零問題。這裏我們可以利用IEEE規定的浮點運算來處理。

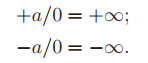
舉個例子，$x_d = 0$且$y_d > 0$時，

$$ t_{xmin} = \frac{x_{min} - x_e}{0} \\ t_{xmax} = \frac{x_{max} - x_e}{0} $$

此時有以下三種情況：

  1. $x_e \leq x_{min} \text{ (no hit)}$
  2. $x_{min} < x_e < x_{max} \text{ (hit)}$
  3. $x_{max} \leq x_e \text{ (no hit)}$

對於第一種情況，區間$(t_{xmin}, t_{xmax}) = (\infty, \infty)$，不會與任何區間重叠，所以沒有與bounding box相交；第二種情況，區間$(t_{xmin},t_{xmax}) = (-\infty, \infty)$，會與任意區間重叠，所以與bounding box相交；第三種情況與第一種情況類似。

這樣看來，利用IEEE的浮點數運算非常有效，但是儅$x_d = -0$時，下面這段代碼就失效了。

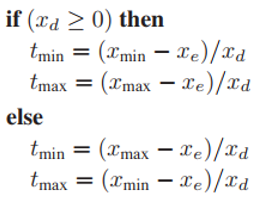
失效的原因在於，在IEEE中，$(-0) == 0$這個判斷是成立的，所以代碼不會按預期進入else分支。爲了解決這個問題，我們便利用$x_d$的倒數對代碼進行修改。

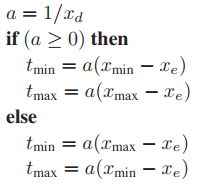
12.3.2 Hierarchical Bounding Box

hierarchical bounding box的基本思想可以看作通過策略將一個軸向bounding box放置在所有物體外。如下圖所示。



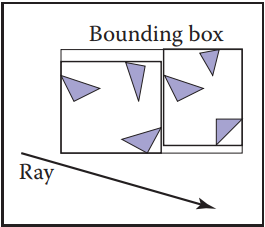
通過劃分不同的物體集合，可以形成不同的bounding box集合，這些集合能夠形成一種樹狀結構。最大的bounding box為根，它包圍著所有物體。根節點的下一級為兩個較小的bounding box，為左子樹和右子樹，就這樣一級級往下劃分。

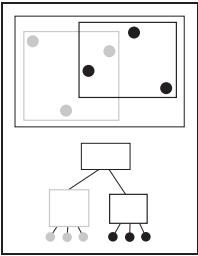
利用這種樹狀數據結構能快速判斷出光纖是否與物體相交、與哪些物體相交。

對於這種層級結構，包圍盒能夠包圍它層級之下的所有物體，但是不能保證包含空間上重叠的所有物體。例如下圖所示。這就導致在嚴格以一維數據排序時，幾何搜索有時比傳統二分搜索來的複雜。本節接下去内容都在不斷優化層級算法，讓其達到最優。

這裏我們假設構建的層級樹為一棵二叉樹，每個節點都有一個bounding box，每個節點要麽是葉節點——包含一個圖元，要麽包含一棵或兩顆子樹。因此樹節點的數據結構可按如下定義。

利用樹結構就能遞歸的查詢光纖是否有被物體遮擋。

上面代碼中需要注意，因爲hit函數繼承surface的虛函數，所以可以為葉節點和内部節點設計不同的hit函數使用。下面來看看如何構建樹，構建樹的原則是：二叉樹，左右子樹盡量平衡，同級節點的box重叠盡量少。一種啓發式的做法就是在劃分為兩棵子樹前先按某個軸進行排序。按照這幾點要求，我們可以得到下面構建樹的實現。

代碼中，我們約定$x$軸為$0$，$y$軸為$1$，$z$軸為$2$。樹的質量與每次選取的軸有很大關係。而選取軸的方法有很多，其中一種是最小化兩棵子樹的bounding box體積。

另一種構建樹的方法是保證左右子樹擁有近似的空間體積而不是要求有相同的物件數量。

儘管這種方式構建的樹會“不平衡”，但是其帶來的好處是更容易遍歷空白區域以及相比排序的開銷來的更小。

12.3.3 Uniform Spatial Subdivision

另一種降低相交測試的開銷方式是空間劃分。這種方法和上面提到的基於物體劃分是有較大區別的：

  • 在hierarchical bounding volumes中，每個物體都只屬於一個節點，但是該物體所占用的空間可能屬於兩個不同的節點；
  • 而在spatial subdivision中，每個空間點都有唯一一個節點，而物體可能屬於許多不同的節點。

基於這個思路，uniform spatial subdivision將場景沿軸向劃分成等尺寸的cell(不一定是立方體)。下圖展示了基於這種方式的光纖相交測試的結果。儅有接觸到物體，遍歷就終止。

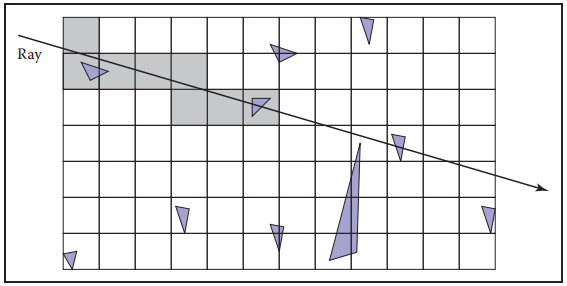
基於這種方式，網格本身應該是surface的子類，并且是一個指向surface的三維數組。對於每個cell，如果未有物體存在，這指針為${\rm Null}$；如果存在一個物體，該指針指向該物體；如果存在多個物體，則該指針可以指向一個物體隊列、另一個網格、或是其他數據結構，如BVH。

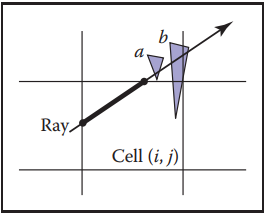
下面説説這種結構的具體實現。假设光线在二维平面下穿过一个$n_x \times n_y$的网格，光线起点在网格外，且传播方向为$x > 0, y > 0$。我們可以先計算出光纖與各條網格綫的交點。

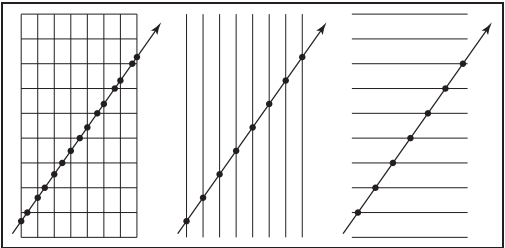
之後，我們要先找到光纖$\mathbf{e} + t\mathbf{d}$射中的第一個cell的索引$(i,j)$，然後按照一定順序遍歷所有單元格。算法的關鍵點在於找到初始cell並確定對$x$還是對$y$遞增。如下圖。根據當前位置與單元格下一個垂直或水平邊界交點即可判斷。例如下圖中，光纖與邊界交點$t_{last}$的下一個交點為水平邊界的$t_{ynext}$，所以下一個cell的索引為$(i,j-1)$。在進行相交測試時，應將$t$限制在當前cell的範圍内。

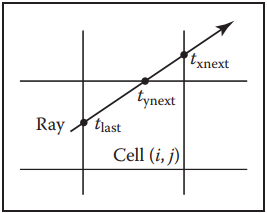
12.3.4 Axis-Aligned Binary Space Partitioning

我們也可采用層級數據結構對空間進行劃分，例如BSP-樹(Binary space partitioning tree)。與之後介紹的可視性排序中使用的BSP-樹類似，這種方式通常用於軸向對齊而不是多邊形對齊的空間劃分進行相交測試。

這種結構中，每個節點包含一個劃分平面，以及左子樹和右子樹。每棵子樹包含了所屬劃分空間下的所有物體。例如，假設劃分平面平行于$yz$軸，劃分位置為$x = D$，那麽該節點結構如下。

在對劃分空間進行相交測試時，存在四種情況。假設光纖為$\mathbf{p} = \mathbf{e} + t\mathbf{d}$

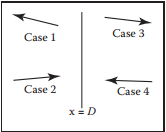
  1. $x_p < D$且$x_d < 0$時，只與左子樹進行相交測試；
  2. $x_p < D$且$x_d > 0$時，先於左子樹進行相交測試，如果未發生相交，再與右子樹進行相交測試，此時我們需要獲得光纖與$x=D$相交的參數，以保證只在子樹範圍内進行相交測試。
  3. $x_p > D$且$x_d > 0$時，與情況1類似；
  4. $x_p < D$且$x_d < 0$時， 與情況2類似。

這樣，相交測試代碼如下。

從上面代碼的輸入參數可以看出，我們需要使光纖射中某些含有bounding box的物體來初始化遍歷過程，即獲得$t_0$和$t_1$。另外，由於劃分平面可能會沿著任意的坐標軸進行，所以可以在bsp-node類中添加一個整數索引$axis$作爲指示。這樣上訴代碼中 $$ x_p = x_a + t_0x_b $$ 可修改為 $$ u_p = a[axis] + t_0b[axis] $$ 這樣做的好處是沒有產生更多的分支。

值得注意的是，儘管處理單個bsp-node比bvh-node快，但是相同位置的平面可能存在多棵子樹中，這就意味著節點數的增加，這樣所占用的内存也就增加。另外遍歷的快慢也與樹構建的質量密切相關。構建BSP-樹和BVH-樹是相似的，我們可以采用之前提到的坐標軸循環方式劃分，也可以對半劃分，還可以嘗試更爲複雜的劃分方式。

12.4 BSP Trees for Visibility

“遮擋"問題，之前使用z-buffer技術在光柵化時處理物體閒的遮擋關係；這裏將介紹使用空間數據結構來確定不同視點下物體的可視順序。

12.4.1 Overview of BSP Tree Algorithm

BSP-樹是一種“畫家”算法——從背景到前景繪製物體。如下圖所示。

畫家算法的框架如下。

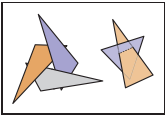
在之前介紹z-buffer技術時也提過畫家算法的缺陷，如下圖中交替重叠的三角形，畫傢算法中的排序將失效。

因此，我們先假設使用BSP-樹時，任意一個多邊形不會“穿過”其他多邊形；在介紹BSP-樹過程中，我們默認圖元為三角形。下面先説説BSP-樹的基本思想。

假設兩個三角形$T_1$和$T_2$，包含三角形$T_1$的平面方程為$f_1(\mathbf{p}) = 0$，該平面將空間分爲兩側，其中一側的所有點$\mathbf{p}^{+}$使$f_1(\mathbf{p}^{+}) > 0$；另一側的所有點$\mathbf{p}^{-}$使$f_1(\mathbf{p}^{-}) < 0$。利用這個特性就能在光路上判斷三角形$T_1$和$T_2$的先後關係。例如，三角形$T_2$的三個點均滿足$f_1(\mathbf{p}) < 0$，則説明$T_2$在$T_1$的一側，那麽繪製順序就與視點$\mathbf{e}$的位置有關。

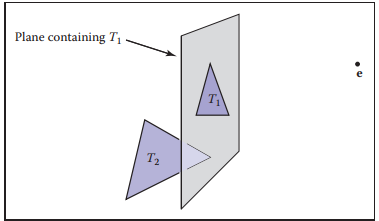
基於這個思想，BSP-樹構建時，假設$T_1$為根，那麽頂點滿足$f_i(\mathbf{p})<0$條件的三角形都存放在$T_1$的負子樹中，而頂點滿足$f_i(\mathbf{p})>0$的三角形存放在$T_1$的正子樹中。這樣我們就很容易根據視點$\mathbf{e}$的位置調整繪製順序。

下面要解釋BSP-樹中，隱式平面的方程表示，因爲不同的表示方式涉及到時間和空間的權衡問題。空間中，平面表示有如下兩種數學表示： $$ f(\mathbf{p}) = ((\mathbf{b} - \mathbf{a}) \times (\mathbf{c} - \mathbf{a})) \cdot (\mathbf{p} - \mathbf{a}) \tag{12.1} $$ $$ f(x, y, z) = Ax + By + Cz + D = 0 \tag{12.2} $$

這兩種表示方式是等價的，對與等式(12.1)，很容易得到平面法向量$\mathbf{n}$為$(\mathbf{b} - \mathbf{a}) \times (\mathbf{c} - \mathbf{a})$，而對於等式(12.2)，法向量$\mathbf{n}=(A, B,Ｃ)$。將平面上一個一直點$\mathbf{a}$帶入兩個方程，很容易得到下面的等式

$$ \begin{align} D & = -Ax_a - By_a - Cz_a\\ & = -\mathbf{n}\cdot \mathbf{a} \end{align} $$

這樣，等式(12.2)就能改寫成：

$$ \begin{align} f(x,y,z) &= \mathbf{n} \cdot \begin{bmatrix}x\\y\\z\end{bmatrix} + D \\ &= \mathbf{n} \cdot \mathbf{p} - \mathbf{n}\cdot\mathbf{a}\\ &= \mathbf{n}\cdot(\mathbf{p}-\mathbf{a})\\ &= 0 \end{align} $$

這就證明了兩等式閒是等效的。兩個方程會導致存儲數據的方案有三種：只存儲頂點；存儲頂點和法向量；存儲法向量、參數$D$和頂點。通常會采用等式(12.1)，這樣只需要存儲三個頂點就足夠了。

而真正影響上面BSP-樹正確工作的并不是平面的表示方式，而是實際情況中兩個三角形不可能不相交，儅遇到這種情況時，會采用後面章節提到的切割技術進行處理，以保證BSP-樹正確運行。

12.4.2 Building the Tree

這裏繼續假設任意兩個三角形不相交，那麽構建BSP-樹的方式能夠按下面這段代碼進行：

現在要來解決三角形被另一個三角形平面截斷的問題。如下圖所示。

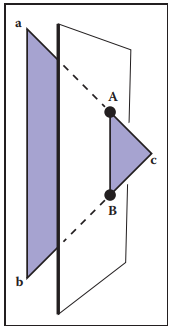
假設三角形的三個頂點為$\mathbf{a}$、$\mathbf{b}$和$\mathbf{c}$，頂點$\mathbf{a}$和頂點$\mathbf{b}$在某個平面的同一側，而頂點$\mathbf{c}$在某個平面的另一側。這樣，三角形就會與平面有兩個交點$\mathbf{A}$和$\mathbf{B}$。我們可以認爲，三角形$\mathbf{a}\mathbf{b}\mathbf{c}$被平面分割成新的三個三角形，如下圖所示。

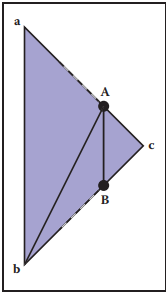
$$ T_1 = (\mathbf{a},\mathbf{b},\mathbf{A}),\\ T_2 = (\mathbf{b},\mathbf{B},\mathbf{A}),\\ T_3 = (\mathbf{A},\mathbf{B},\mathbf{c}), $$

注意，這裏頂點順序對於法向量的方向至關重要，要保證新生成的三角形法向量與原始三角形一致。如果我們認爲$f(\mathbf{c})<0$，那麽基於上面構建樹的方式，新生成的三角形將分別加入到正子樹或負子樹中。

$$ \text{positive-subtree = node}(T_1)\\ \text{positive-subtree = node}(T_2)\\ \text{negative-subtree = node}(T_3) $$

實際使用過程中，如果使用上面代碼中的判斷條件過於嚴苛，通常會在分割平面周圍取一個$\epsilon$的緩衝區，這樣保證三角形被分割平面截取的部分極少時，不會裂變出新的三角形而增加開銷。新的代碼如下。

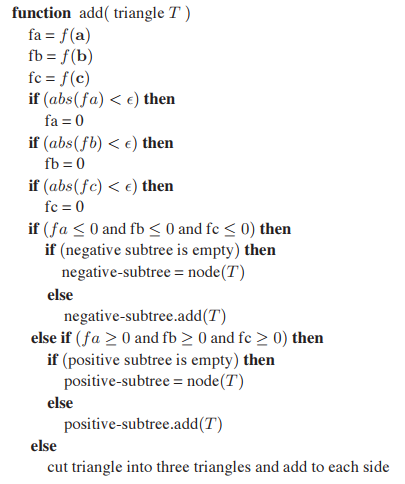
12.4.3 Cutting Triangles

上節代碼最後提到，如果所有測試條件不滿足，將進行三角形拆分並添加到對應子樹中；這看起來非常簡單，但是過程繁瑣。爲了充分發揮BSP-樹可以預先構建的優勢，我們可以忽略構建效率來進行這部分操作。假設頂點$\mathbf{c}$與另外兩個頂點不在同一側是標準形式，那麽通過swap操作轉爲該標準形式后，就可以進行三角形拆分，最後根據$f_c$的符號，將拆分後三角形添加到不同子樹中。具體代碼如下：

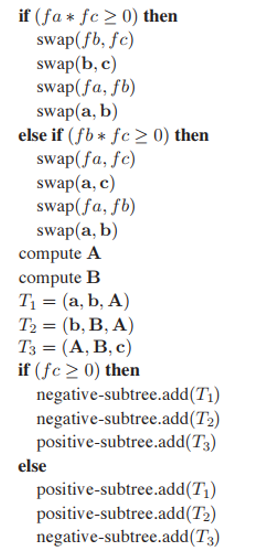
注意，這裏有個細節問題需要討論，儅其中一個頂點正好位於分割平面上時($f_i = 0$)，上面代碼依然奏效，但是拆分出的其中一個三角形面積為$0$，雖然這種情況并不危險，因爲光柵化必須對$0$面積圖元進行處理，但是我們也能將其排除添加到BSP-樹中，或者遇到此類情況($f_a$, $f_b$,$f_c$中有一個為$0$)，我們只拆分出兩個三角形。這種特殊情況如下圖所示。

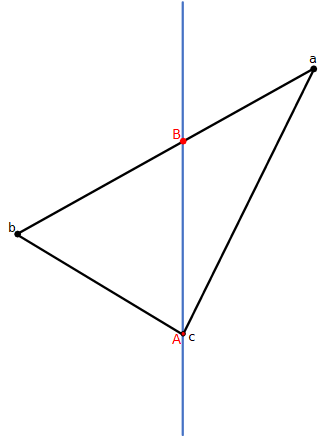
計算交點$\mathbf{A}$和$\mathbf{B}$的方式如下。定義綫段$\mathbf{a}\mathbf{c}$方程為： $$ \mathbf{p}(t) = \mathbf{a} + t(\mathbf{c}-\mathbf{a}) $$

分割平面方程為： $$ \mathbf{n}\cdot \mathbf{p} + D = 0 $$

也許會好奇爲什麽要用這種形式表示，而不是用之前提到的等式(12.1)表示，應爲這裏的$D$是由不同三角形決定的，所以使用$D$而不是$\mathbf{n}\cdot\mathbf{a}$。

那麽將點$\mathbf{p}(t)$帶入分割平面方程中就可解得$t$： $$ t = -\frac{\mathbf{n}\cdot\mathbf{a} + D}{\mathbf{n}\cdot(\mathbf{c} - \mathbf{a})} $$

這樣將$t$代囘$\mathbf{p}(t)$中即可求得$\mathbf{A}$點坐標。同理可得到$\mathbf{B}$點坐標。

12.4.4 Optimizing the Tree

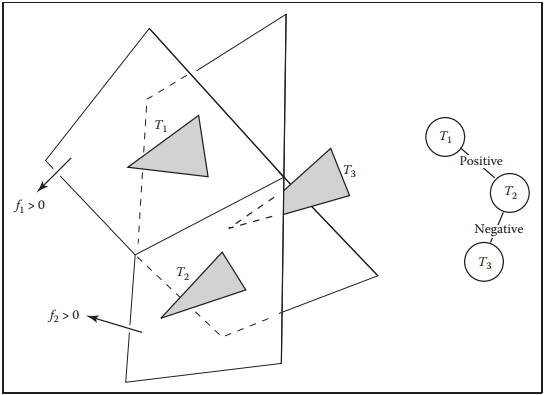
上面已經將BSP-樹的構建和遍歷都大致梳理清楚，這裏將繼續討論效率問題。實際上，相比遍歷樹，我們並不在意構建樹的效率，因爲這是個預處理過程。但是，遍歷樹的效率與節點數成正比（無論是否是平衡樹），而節點數量又與添加三角形的順序有關。如下圖中，若以$T_1$為根節點，那麽該BSP-樹只有兩個節點；若以$T_2$為根節點，那麽三角形$T_1$會被拆分，那麽節點數量將增加。

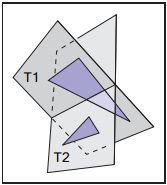
雖然知道了節點添加順序影響最終遍歷效率，但是很難找到一種好的添加順序，因爲如果存在$N$個節點，那麽節點順序將有$N!$種，依次測試這些添加順序顯然是不現實的，實際做法是隨機挑選若干種添加順序，在這些結果中選取最優的樹。

另外一個可優化的地方就是三角形拆分部分，我們可以將其拆分成一個三角形和一個任意四邊形，當然如果模型都是由三角形構成時，這麽做並不合適，但是如果存在任意多邊形構成，那麽這種方式在一定程度上可以提高效率。

12.5 Tilling Multidimensional Arrays

这里先提个概念：TLB(转译后备缓冲器)；這個緩衝器的使用與算法性能息息相關。簡單的說就是多維數組在内存中的存儲方式本質上都是按一維數組方式存放，由於内存訪問機制的限制，多維數組從不同維度遍歷整個數組的效率是不同的。例如下圖中大小爲$N_x \times N_y$的二維數組，同一行相鄰的兩個數據在内存中是順序存儲，同一列相鄰的兩個數據在内存中相差$N_x$，這就導致儅内存預讀數據量小於$N_x$時，兩者訪問效率顯著不同。

爲了讓行列的局部访问效率相当，一种标准的解决方案是tiles技术，类似将一个大的二维数组切割成若干个小的二维数组。如下图所示。这个做法的一个关键问题是，每个tile的尺寸要设计多大？这个通常与机器的内存单元尺寸相关。例如，某机器内存缓冲区大小为128-byte，我们数据类型大小为2-byte，那么tile的尺寸就能选择$8\times 8$。如果数据类型大小为4-byte，那么tile的长度为32，使用$5\times 5$略小，而使用$6\times 6$又略大。

12.5.1 One-Level Tiling for 2D Arrays

假设一个$N_x \times N_y$的二维数组，将其拆分成若干个$n \times n$的tiles。如下图所示。那么每个维度tile的数量可以按如下方式计算：

$$ B_x = N_x / n, \\ B_y = N_y / n. $$

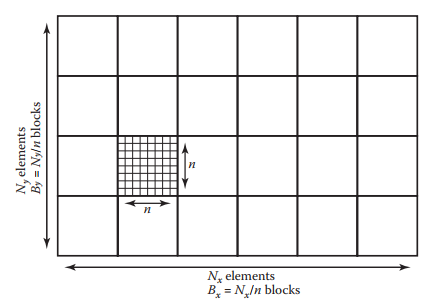
如果$n$不能被$N_x$和$N_y$整除，那么我们需要在一些边界tile内填充一些数据。例如，$N_x = 15$且$n= 4$，那么$N_x$需要填充至$16$。

下面介绍如何获得原图中$(x,y)$的索引。首先计算$(x,y)$所在的tile索引$(b_x, b_y)$。

$$ b_x = x \div n,\\ b_y = y \div n $$

这里$\div$表示整除运算。这样，$(b_x,b_y)$tile的首个元素的索引值为： $$ {\rm index} = n^2(B_xb_y + b_x) $$

接着计算在$(b_x, b_y)$tile内的坐标：

$$ x’ = x\text{ mod }n,\\ y' = y\text{ mod }n $$

那么，偏移量为： $$ {\rm offset} = y’ n + x' $$

这样就得到了最终索引值：

$$ \begin{align} {\rm index} &= n^2(B_x b_y + b_x) + y'n + x'\\ &= n^2((N_x \div n)(y \div n) + (x \div n)) + (y\text{ mod }n) n + (x\text{ mode }n) \end{align} $$

该索引值计算使用了大量的整数乘法、除法和模运算，这个开销在一些处理器中是巨大的。如果$n$是$2$的倍数，那么这些操作可以转换成位运算。但这个条件往往不满足。如果使用增量式计算，那么需要追踪额外的计数器，做大量的比较运算和较差的分支预测能力。当然，并非没有解决方案，我们将上面的索引计算进行拆分： $$ {\rm index} = F_x(x) + F_y(y) $$

其中，

$$ F_x(x) = n^2(x \div n) + (x \text{ mod } n),\\ F_y(y) = n^2(N_x \div n)(y \div n) + (y \text{ mod } n)n $$

这样，我们可以对$F_x$和$F_y$进行制表，然后通过查表获得$(x,y)$的索引值。

12.5.2 Example: Two-Level Tiling for 3D Arrays

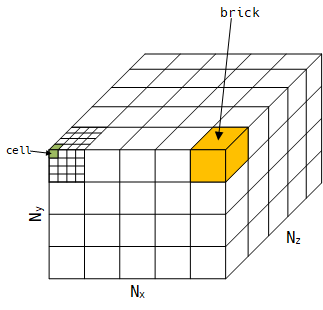
假設一個三維數組為$(N_x, N_y, N_z)$，爲了提高TLB命中率，將其劃分爲$m \times m \times m$個bricks，每個brick劃分為$n \times n \times n$個cells。如下圖所示：

那麽點$(x,y,z)$在tiles方式下的索引值為：

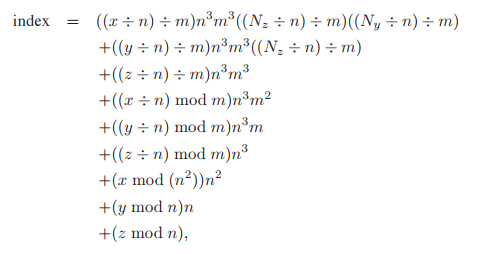
利用二維數組中的方式，將索引計算進行拆分，然後分別對拆分部分進行制表。 $$ {\rm index} = F_x(x) + F_y(y) + F_z(z) $$

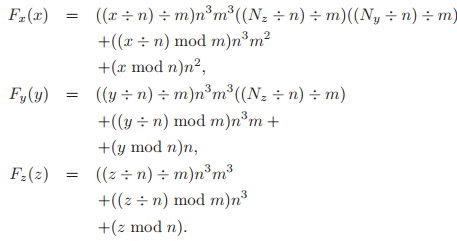
Frequently Asked Questions

聲明

該文檔是本人閲讀書籍《Fundamentals of Computer Graphics, Fourth_Edition》和學習課程《Games-101：现代计算机图形学入门》時整理的閲讀筆記，文檔中所有圖片主要來自本書截圖、Games-101課件截圖和網絡公開圖片。若發現錯誤，歡迎討論指正：uninitmatrix@gmail.com。