符号约定

  • WCS —— 世界坐标系
  • CCS —— 相机坐标系
  • IPCS——像平面坐标系
  • ICS——图像坐标系
  • $(x_w, y_w, z_w)$ ——世界坐标系点坐标
  • $(x_c, y_c, z_c)$——相机坐标系点坐标
  • $(u,v)$——像平面坐标系点坐标
  • $(\tilde{u}, \tilde{v})$——像平面坐标系畸变后点坐标
  • $(r,c)$——图像坐标系点坐标
  • $f$——相机常量或主距
  • $(c_x,c_y)$——图像主点

引言

为了对摄像机进行标定，首先需要构建一个模型，这个模型由镜头、图像传感器(CCD或CMOS)和采集卡(如果使用)组成，利用这个模型可以将世界坐标系中三维空间点投影到二维图像上。

在机器视觉领域，镜头常用的有两种类型：普通镜头和远心镜头。两者区别在于：普通镜头实现世界坐标系到图像坐标系的透视投影；而远心镜头则是平行投影。我们称图像传感器与普通镜头的组合为针孔摄像机模型，而图像传感器与远心镜头的组合称为远心摄像机模型。

模型中另一个组成部分——图像传感器，其可分为：线阵图像传感器和面阵图像传感器。使用面阵图像传感器时，普通镜头和远心镜头都非常常用；而使用线阵图像传感器时，只有普通镜头比较常用，我们常将这种组合称为线扫描摄像机。

下面重点说明针孔面阵摄像机模型，线扫描摄像机模型以及远心镜头模型不做阐述。 　　

面阵摄像机模型

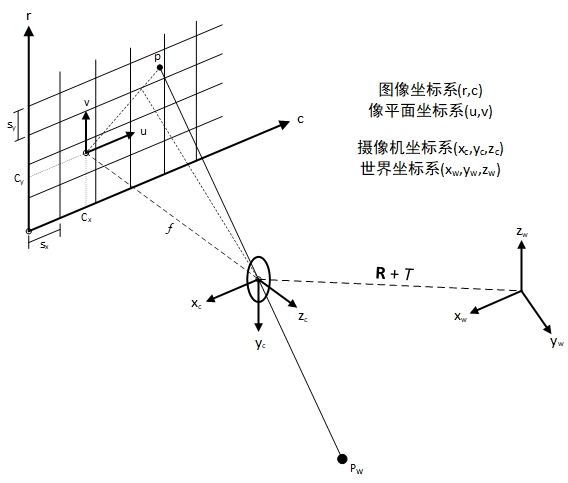
图(1.1)展示了一个针孔相机模型的透视投影关系。世界坐标系中点$P_W$通过镜头投影到像平面上的点$p$。若图像无畸变，则点$p$应在$P_W$与投影中心连线的延长线上；若图像发生畸变，则点$p$的位置将发生偏移，如图中虚线所示。

现在投影平面与被测物分居镜头两侧，为了便于计算，通常将投影平面移至与被测物同侧。如图(1.2)所示。这样可让图像坐标系与像素坐标系对齐。

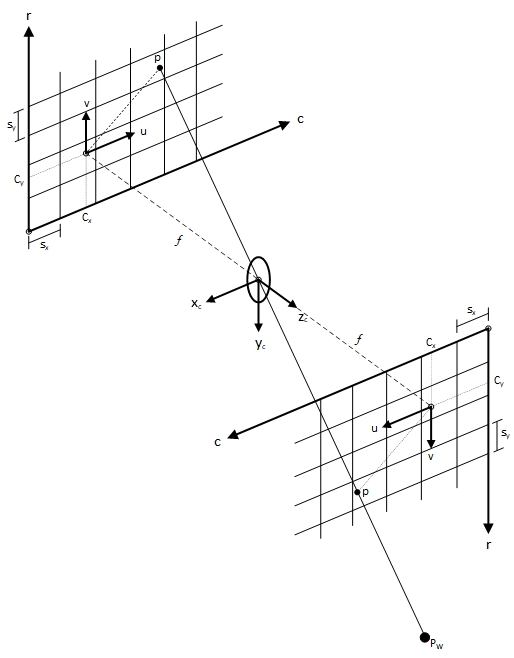
三维物体向二维平面投影过程可分为两步。首先，由于点$P_W$在世界坐标系(WCS)中，需将其转换到相机坐标系(CCS)中。之后，再由相机坐标系转换到图像坐标系中。下面分别推导这两个过程中的投影关系及可确认的参数。

通常认为，从世界坐标系到相机坐标系的变换为刚性变换，即由平移和旋转变换组成。那么相机坐标系中点$P_C(x_c,y_c,z_c)$与世界坐标系中点$P_W(x_w,y_w,z_w)$的关系为：

$$ \begin{equation} P_C = R * P_W + T \tag{1} \end{equation} $$

其中，$T=(t_x, t_y,t_z)^T$为平移向量，$R=R(\alpha, \beta, \gamma)$为旋转矩阵。$\alpha$为绕$x$轴旋转角度，$\beta$为绕$y$轴旋转角度， $\gamma$为绕$z$轴旋转角度。其展开表达式如下：

$$ R(\alpha, \beta,\gamma) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos{\alpha} & -\sin{\alpha} \\ 0 & \sin{\alpha} & \cos{\alpha} \end{pmatrix}\begin{pmatrix} \cos{\beta} & 0 & \sin{\beta} \\ 0 & 1 & 0 \\ -\sin{\beta} & 0 & \cos{\beta} \end{pmatrix}\begin{pmatrix} \cos{\gamma} & -\sin{\gamma} & 0 \\ \sin{\gamma} & \cos{\gamma} & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

$(\alpha, \beta, \gamma, t_x, t_y, t_z)$这六个参数称为摄像机外参、外方位参数或摄像机位姿，它们反映了相机坐标系与世界坐标系间相对位置关系。

之后，将点$P_C$从相机坐标系投影到像平面坐标系(IPCS)中。这个投影通常为透视投影。参考图1.2，此时点$P_W$因已转换到相机坐标系，所以变为点$P_C$。通过相似三角形，可得：

$$ \begin{equation} \begin{pmatrix} u \\ v \end{pmatrix} = \frac{f}{z_c}\begin{pmatrix} x_c \\ y_c \end{pmatrix} \tag{2} \end{equation} $$

其中$f$表示相机常量或主距，并不是相机焦距。

(PS: 若仍无法理解上式如何得到，参考下图运用相似三角形)

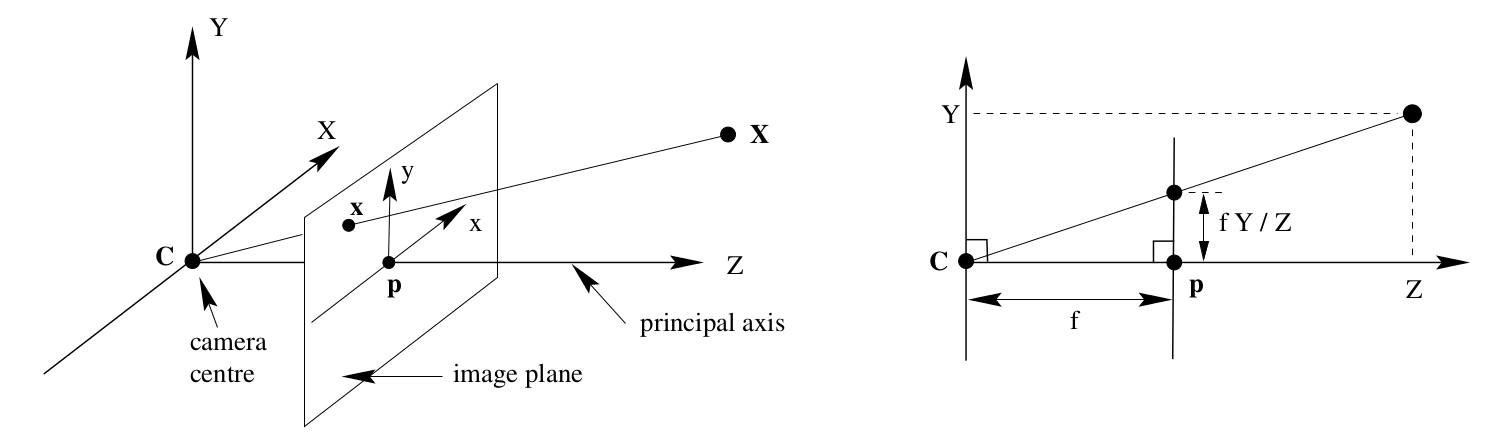
这里继续，由于镜头的畸变，会导致坐标$(u,v)^T$发生变换。常用畸变模型将在下节简要说明，这里将用Division模型做说明，因为该模型只需考虑一个参数$\kappa$，其为正值，畸变为枕形畸变；若为负值，畸变为桶形畸变。畸变后的坐标为：

$$ \begin{equation} \begin{pmatrix} \tilde{u} \\ \tilde{v} \end{pmatrix} = K \begin{pmatrix} u \\ v \end{pmatrix} \tag{3} \end{equation} $$

其中， $K$是关于$\kappa$的畸变系数。

最后将点$(u,v)^T$从像平面坐标系转换到图像坐标系(ICS)中：

$$ \begin{equation} \begin{pmatrix} r \\ c \end{pmatrix} = \begin{pmatrix} \frac{1}{s_y} & 0 \\ 0 & \frac{1}{s_x} \end{pmatrix} \begin{pmatrix} \tilde{v} \\ \tilde{u} \end{pmatrix} + \begin{pmatrix} c_y \\ c_x \end{pmatrix} = \begin{pmatrix} \frac{\tilde{v}}{s_y} + c_y\\ \frac{\tilde{u}}{s_x} + c_x \end{pmatrix} \tag{4} \end{equation} $$

式中，$s_x$和$s_y$是缩放比例因子。对于针孔摄像机模型，它们是图像传感器上水平和垂直方向上相邻像素之间的距离。点$(c_x,c_y)^T$是图像的主点。对于针孔摄像机而言，该点是投影中心在像平面上的垂直投影，也就是该点与投影中心连线与像平面垂直。同时这个点也是径向畸变的中心。至此，针孔相机模型的内参都已确定，其包括$(f,\kappa,s_x,s_y,c_x,c_y)$这六个参数。它们确定了摄像机如何实现三维空间点到二维图像点的投影。

这里特别说明下，由于畸变模型是选用Division模型，所以内参中的畸变参数只有一个$\kappa$。若选用其它畸变模型，畸变参数将会有不同个数。因此内参并不是固定六个参数。

讲了这么多，那么总结下，整个相机模型的建立，就是将从空间点到图像上点的映射提炼成一个函数表示。那这个函数的表示如下：

$$ \begin{equation} z_c \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} = \underbrace{\begin{pmatrix} \frac{f}{s_x} & 0 & c_x \\ 0 & \frac{f}{s_y} & c_y \\ 0 & 0 & 1 \end{pmatrix}* \underbrace{\begin{bmatrix} R | T \end{bmatrix} *\begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix}}_{世界坐标系转换到相机坐标系} }_{相机坐标系转换到无畸变像平面坐标系} \tag{5} \end{equation} $$

畸变模型

畸变是镜头固有的属性。理论上是存在一种不引入任何畸变的镜头，但是，现实中，由于制造工艺等因素，这种理想镜头又是不存在的。一般对畸变分类可分为：径向畸变与切向畸变。径向畸变来源于透镜的形状；切向畸变则来自整个摄像机的组装过程[2]。

(PS: 本节只是错略介绍畸变模型，具体畸变模型如何构造和推导的，不做深入研究。如有兴趣，请自行查阅相关资料，本节也会给出一些参考文献)

径向畸变

这种畸变会使不经过光轴的直线，通过镜头后成的像不再是一条直线。通常根据一个矩形成像后的特征可以定义两种畸变：枕形畸变和桶形畸变。参考图1.3。

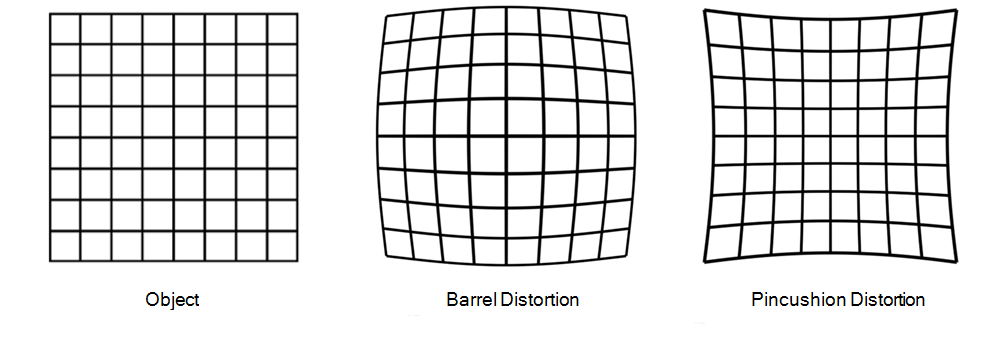
对于大多数镜头而言，它们的畸变都可以充分地近似为径向畸变[3]。

切向畸变

切向畸变的产生，是由于透镜制造过程中，透镜本身与传感器平面不平行造成的。

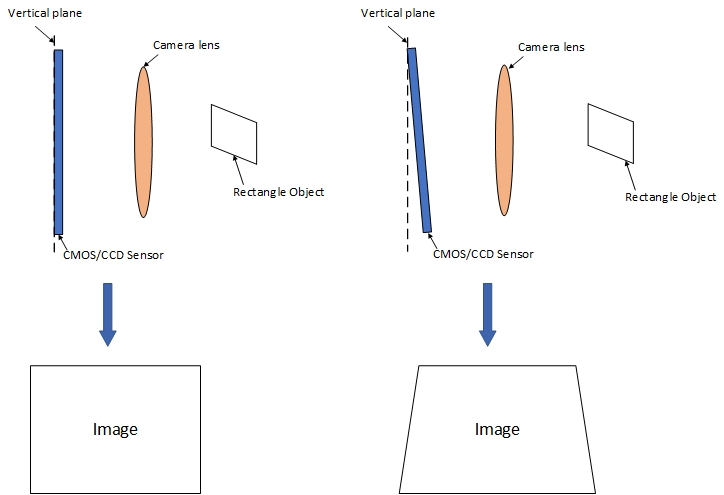
Division畸变模型

Division模型在前面建立面阵摄像机模型时已经简略提到。其完整表达如下：

$$ \begin{equation} \begin{pmatrix} \tilde{u} \\ \tilde{v} \end{pmatrix} = \frac{2}{1+\sqrt{1-4\kappa(u^2 + v^2)}} \begin{pmatrix} u \\ v \end{pmatrix} \tag{6} \end{equation} $$

该模型几乎可以表示所有在机器视觉应用中常用镜头的畸变(仅支持径向畸变)[4]，并且足够准确。其参数$\kappa$表示了径向畸变量级。如果$\kappa$为负值，畸变为桶形畸变；如果$\kappa$为正值，那畸变为枕形畸变。另外与其他模型相比，有一个极大的优点就是，可以通过下式进行畸变校正[1]：

$$ \begin{equation} \begin{pmatrix} u \\ v \end{pmatrix} = \frac{1}{1+\kappa(\tilde{u}^2 + \tilde{v}^2)} \begin{pmatrix} \tilde{u} \\ \tilde{v} \end{pmatrix} \tag{7} \end{equation} $$
该模型也是Halcon中calibrate_cameras()算子的标配。如果想详细了解该模型，参考论文[5]。

多项式畸变模型

该模型利用泰勒级数，将畸变函数在$r=0$处展开为多项式，该多项式的通用形式为：$f(r) = a_0 + a_1r+a_2r^2 + \cdots $，当$r=0$时，$f(r) =0 $，这意味着$a_0 = 0$。又因为函数必须关于$r$径向对称，所以，只有$r$的偶次幂不为0。因此，畸变函数只需要用$r^2$，$r^4$和$r^6$项的系数来描述。该模型也是OpenCV中，标定函数所使用的模型。该模型理论基础和推导可参考文献[6]、[7]。

多项式畸变模型数学表达如下：

$$ \begin{equation} \begin{matrix} u = \tilde{u}\left( 1 + k_1 \tilde{r}^2 + k_2\tilde{r}^4 + k_3 \tilde{r}^6\right) + \left( p_1(\tilde{r}^2 + 2\tilde{u}^2)+2p_2\tilde{u}\tilde{v} \right)\\[2ex] v = \tilde{v}\left(1 + k_1 \tilde{r}^2 + k_2\tilde{r}^4 + k_3 \tilde{r}^6 \right) +(2p_1\tilde{u}\tilde{v} + p_2(\tilde{r}^2 + 2\tilde{v}^2)) \end{matrix} \tag{8} \end{equation} $$

其中$\tilde{r}^2 = \tilde{u}^2 + \tilde{v}^2$，$k_1$、$k_2$、$k_3$、$k_4$、$k_5$和$k_6$为径向畸变参数，$p_1$和$p_2$为切线畸变参数。

多项式模型虽然能很好地表征径向、切向畸变，但是当从畸变坐标变换为原始坐标过程将变得十分困难，这里需要用到数值寻根算法，这导致该模型要比Division模型来的低效[4]。

标定过程

至此之前的讨论，已经构建了一套完善的模型。可以看出，整个标定过程就是利用这个模型去确定摄像机内参和外参的过程。这个过程必须已知世界坐标系中足够多的三维空间点的坐标，找到这些空间点在图像中的投影点的二维图像坐标，并建立对应关系。获得世界坐标系中的三维点坐标，往往将容易提取特征的目标物体或标志放置在一个已知位置上。而测量物的绝对坐标一般不重要，只要知道测量物与相机的相对位置已经足够用来精确测量。因此 ，通常使用已经事先精确测量过的已知尺寸的可移动的标定板来标定相机。这种方式优势在于，可以在相机固定的情况下进行标定。

在确定世界坐标系中已知点与它们在图像中投影的对应关系，这个过程较为困难。因此，标定板的结构一般都尽量使确定对应关系的过程更简单。常用的标定板有以下两种：圆点阵列以及棋盘格。

这种平面标定板的好处在于，首先，它们易于操作；第二，它们的尺寸可以制作的非常精确；最后，它们可以非常方便的应用在背光照明条件下。

以圆点阵列标定板为例，其外围黑色矩形边界框将标定板的内部区域与背景分开，可以利用这一特性在图像中定位标定板位置。之后通过简单的阈值分割可以找到标定板内部区域。阈值的选取可以自动尝试，直至找到$m \times n$个孔洞为止。一旦确定了内部区域，就可使用亚像素边缘提取方法来提取标定板各个圆点的边缘。因为圆形标定标记的投影为椭圆，可以使用较为强健的椭圆拟合算法对边缘进行拟合。最后，基于提取出椭圆的最小外接四边形，可以非常容易确定标定标记与它们在图像中投影之间的对应关系。在确定了标定标记与它们图像中投影的对应关系后，就可以进行相机标定了。

而棋盘格标定板提取标定标记的过程也类似。这里不做过多展开。

下面详细介绍下非常有名的张氏标定法[8]。

张氏标定法

“张氏标定法"是张正友教授于1998年在其论文[8]中提出的，利用单平面棋盘格(或圆点阵列)对相机进行标定。该方法不仅灵活，而且具有很高的精度。该方法只需要至少两张标定图片即可，同时相机或者标定平面可以随意移动。也是因为有这些优点，该方法已作为工具箱或封装好的函数被广泛使用。

其从公式出发：

$$ \begin{equation} s \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} = A* \begin{bmatrix} R | T \end{bmatrix} *\begin{pmatrix} x_w \\ y_w \\ z_w \\ 1 \end{pmatrix} \tag{9} \end{equation} $$

其中， $s=z_c$为任意的缩放因子，

$$ A = \begin{pmatrix} \frac{f}{s_x} & r & c_x \\ 0 & \frac{f}{s_y} & c_y \\ 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} m & r & c_x \\ 0 & n & c_y \\ 0 & 0 & 1 \end{pmatrix} $$

矩阵$A$与公式(5)中的内参矩阵略为不同，其中参数$r$表示两条图像轴的倾斜因子。模型建立过程为理想情况，所以公式(5)中默认为$0$。为了之后推导的方便，令$\frac{f}{s_x} = m$、$\frac{f}{s_y} = n$。

假定，物体所在平面为$z_w=0$平面，那么公式(9)可简化为：

$$ \begin{equation} s \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} = A* \begin{bmatrix} r_1 & r_2 & r_3 & t \end{bmatrix} *\begin{pmatrix} x_w \\ y_w \\ 0 \\ 1 \end{pmatrix} = A * \begin{bmatrix} r_1 & r_2 &t \end{bmatrix} * \begin{pmatrix} x_w \\ y_w \\ 1 \end{pmatrix} = H*\begin{pmatrix} x_w \\ y_w \\ 1 \end{pmatrix} \tag{10} \end{equation} $$

其中，

$$ H = A\begin{bmatrix} r_1 & r_2 & t \end{bmatrix} $$

$H$为一个$3\times3$的单应性矩阵。再令，

$$ \begin{equation} \begin{bmatrix} h_1 & h_2 & h_3 \end{bmatrix} = \lambda A \begin{bmatrix} r_1 & r_2 & t \end{bmatrix} \tag{11} \end{equation} $$

$\lambda$为比例因子。由公式(11)可得，

$$ \lambda = \frac{1}{s} \\ h_1 = \lambda A r_1 \Rightarrow r_1 =sA^{-1}h_1 \\ h2 = \lambda A r_2 \Rightarrow r_2 =sA^{-1}h_2 $$

由于从世界坐标系变换到相机坐标系为刚性变换，所以$r_1$与$r_2$标准正交，那么，

$$ \begin{equation} \begin{matrix} r_1^T r_2 = 0 \Rightarrow h_1^TA^{-T}A^{-1}h_2 = 0 \\[2ex] ||r_1|| = ||r_2|| = 1 \Rightarrow h_1^TA^{-T}A^{-1}h_1 = h_2^TA^{-T}A^{-1}h_2 \end{matrix} \tag{12} \end{equation} $$

这里， 令

$$ B = A^{-T}A^{-1} = \begin{bmatrix} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{bmatrix} = \begin{bmatrix} \frac{1}{m^2} & -\frac{r}{m^2n} & \frac{c_y r - c_xn}{m^2n} \\ -\frac{r}{m^2n} & \frac{r^2}{m^2n^2}+\frac{1}{n^2} & -\frac{r(c_yr - c_xn)}{m^2n^2}-\frac{c_y}{n^2}\\ \frac{c_yr-c_xn}{m^2n} & -\frac{r(c_yr-c_xn)}{m^2n^2}-\frac{c_y}{n^2} & \frac{(c_yr-c_xn)^2}{m^2n^2} +\frac{c_y^2}{n^2} + 1 \end{bmatrix} $$

仔细观察可发现，矩阵**$B$**为对称阵，那么可用一个6维向量表示： $$ b = [B_{11},B_{12},B_{22},B_{13},B_{23},B_{33}]^T $$

矩阵**$H$**的第$i$列可表示为: $$ h_i = [h_{i1}, h_{i2}, h_{i3}]^T $$

因此可推导出： $$ h_i^TBh_i = v_{ij}^Tb $$

其中，

$$ v_{ij} = \begin{bmatrix} h_{i1}h_{j1}\\ h_{i1}h_{j2} + h_{i2}h_{j1} \\ h_{i2}h_{j2} \\ h_{i3}h_{j1} + h_{i1}h_{j3} \\ h_{i3}h_{j2} + h_{i2}h_{j3} \\ h_{i3}h_{j3} \end{bmatrix} $$

式(12)的两个约束条件可化为：

$$ \begin{equation} \begin{bmatrix} v_{12}^T \\ (v_{11}-v_{22})^T \end{bmatrix}b = 0 \Rightarrow Vb = 0 \tag{13} \end{equation} $$

若标定过程中，获取了$n$张标定图像，则矩阵$V$大小为$2n \times 6$。因为未知参数共5个：$m,n,r,c_x,c_y$。为了完全解出，至少需要$n\geq3$幅图像，即$3$个单应矩阵在$2$个约束条件下可有$6$个方程。因此，实际操作中，要获取$3$个单应矩阵，需通过改变相机与标定板的相对位置来获取。若只有$2$张图片，可假定参数$r=0$(图像轴未发生倾斜)同样也能求解。若$n=1$时，只能求解出两个相机内参，例如：假设图像轴未发生倾斜($r=0$)， 主点位置位于图像中心，这样就能求解出内参$m,n$。

一般的情况下，公式(13)运用Cholesky分解，就可得到内参的一般化公式：

$$ \begin{align} c_y &= \frac{(B_{12}B_{13}-B_{11}B_{23})}{B_{11}B_{22} - B_{12}^2} \\ \lambda &= B_{33} - \frac{B_{13}^2 + c_y (B_{12}B_{13}-B_{11}B_{23})}{B_{11}} \\ m &= \sqrt{\frac{\lambda}{B_{11}}} \\ n &= \sqrt{\frac{\lambda B_{11}}{B_{11}B_{22} - B_{12}^2}} \\ r &= -\frac{B_{12}m^2n}{\lambda} \\ c_x &= \frac{rc_y}{m}-B_{13}\frac{m^2}{\lambda} \end{align} $$

一旦内参确定了，那么每张图的外参可以根据下面式得到：

$$ \begin{align} r_1 &= \lambda A^{-1}h_1 \\ r_2 &= \lambda A^{-1}h_2 \\ r_3 &= r_1 \times r_2 \\ t &= \lambda A^{-1} h_3 \end{align} $$

其中，$\lambda = \frac{1}{||A^{-1}h_1||} = \frac{1}{||A^{-1}h_2||}$

由于数据点中存在噪声，旋转矩阵$R = [r_1, r_2, r_3]$并不满足旋转矩阵的特征，如果需要，可通过SVD获取最优旋转矩阵。

以上的推导结论仅仅是理论上通过最小化代数距离得到的，并没有物理意义。也就是说，因为噪声的存在，理论解与真实解间存在偏差，这个偏差在论文中采用了最大似然估计 (Maximum-Likelihood Esitmation)进行优化。

由于张教授略过了中间过程，直接给出公式：

$$ \begin{equation} \sum_{i=1}^{n}\sum_{j=1}^{m}||m_{ij} - \hat{m}(A, R_i, t_i, M_j)||^2 \tag{14} \end{equation} $$

其中，$m_{ij}$表示第i张标定图像中的第j个角点；$\hat{m}(A, R_i, t_i, M_j)$表示第i张图像中，世界坐标系下点$M_j$在图像上的投影点。最小化式(14)是一个非线性最小化问题，可通过Levenberg-Marquardt Algorithm[9]求解。

PS：因为最大似然估计这部分也还没搞得特别明白，就不多说了。

相机参数的准确度

在张氏标定法中，如果要估计出所有内参，只要至少3幅图像就能得到。但是现实的残酷性再次提醒我们，由于标定过程中，标定板的位置摆放不适当的话，将导致简并性配置，即相机参数中的某个参数或某些参数无法得到唯一值。为了得到高准确度的相机参数，就必须避免这种情况的发生。行之有效的办法就是改变标定图像的数量。下图显示了图像数量对标定参数的影响。

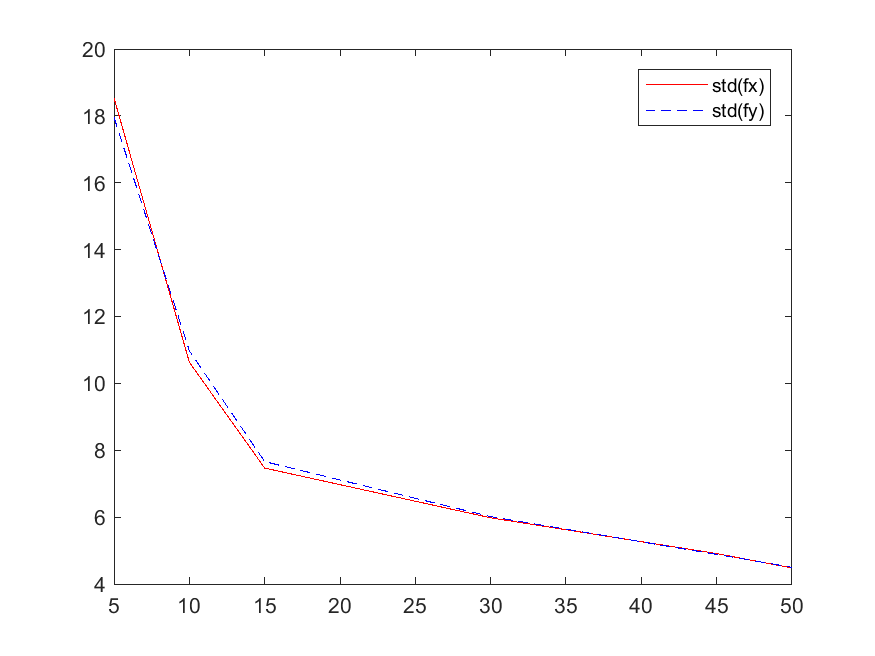
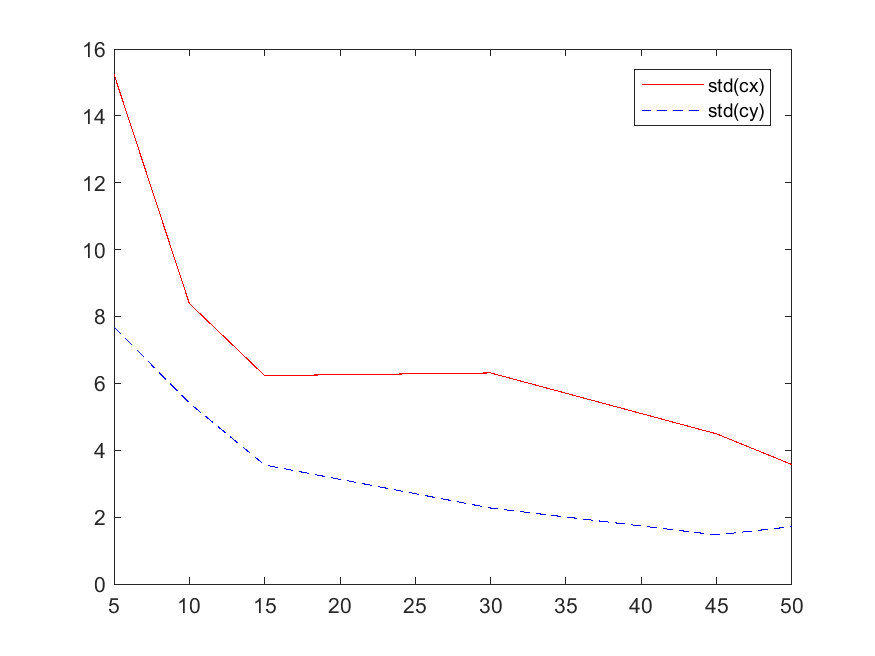
图中分别显示了主距$f_x,f_y$和主点$c_x,c_y$的标准差。改数据来源于拍摄了52幅标定板图像。然后使用这52幅图像中包含$k$幅图像$(k = 5,10,15,30,45,50)$的子集来标定摄像机，每个子集随机抽样$n$次(n=20)。(PS: 这种数据分析的方式还比较粗糙，后期会找时间改改，但是总体趋势还是正确的)。可以看出，相机参数的准确度随着使用图像数量的增加而明显增加。因此，为了得到更精确的相机参数，就需要更多的标定图像。我一般会选取20张。而且，标定板在标定图像中最好能够覆盖整个视野并尽可能覆盖相机外参的范围。如果标定板能够在标定图像中覆盖图像的每个角落，可以使得计算得到的畸变系数更准确。如果标定板可以覆盖较大的深度范围，那么所有的相机参数都会更准确。可以通过将标定板绕它的$x$轴和$y$轴旋转或者将标定板放置在与相机不同距离的位置上使标定板覆盖较大的深度范围。[1]

另外，文献[1]中，作者同样通过实验的方式得出，调节相机镜头的$f$值后，需要对相机进行重新标定，至少对某些镜头而言是必须的。这里就不展开说明了，记住结论就好！

参考文献

[1] 《机器视觉算法与应用》

[2] 《Learning OpenCV》

[3] Lenz R, Fritsch D. Accuracy of videometry with CCD sensors[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1990, 45(2): 90-110.

[4] Steger C. A comprehensive and versatile camera model for cameras with tilt lenses[J]. International Journal of Computer Vision, 2017, 123(2): 121-159.

[5] Fitzgibbon A W. Simultaneous linear estimation of multiple view geometry and lens distortion[C]//Computer Vision and Pattern Recognition, 2001. CVPR 2001. Proceedings of the 2001 IEEE Computer Society Conference on. IEEE, 2001, 1: I-I.

[6] Duane C B. Close-range camera calibration[J]. Photogramm. Eng, 1971, 37(8): 855-866.

[7] Brown D C. Decentering distortion of lenses[J]. Photogrammetric Engineering and Remote Sensing, 1966.

[8] Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22(11): 1330-1334.

[9] Moré J J. The Levenberg-Marquardt algorithm: implementation and theory[M]//Numerical analysis. Springer, Berlin, Heidelberg, 1978: 105-116.